【2024春人教七下数学精品教案】5_3_1 平行线的性质
文档属性
| 名称 | 【2024春人教七下数学精品教案】5_3_1 平行线的性质 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.3.1 平行线的性质 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第五章“相交线与平行线” 5.3.1平行线的性质,内容包括:平行线的性质;平行线的判定和性质综合应用.
2.内容解析
《平行线的性质》人教版七年级数学下册的内容,本节课是在学生已经学习了同位角、内错角、同旁内角和平行线的判定的基础上进行教学的.这节课是空间与图形领域的基础知识,在以后的学习中经常要用到.它为今后三角形内角和、三角形全等、三角形相似等知识的学习奠定了理论基础,学好这部分内容至关重要。在这节课的学习中,我先组织学生利用手中的量角器对“两直线平行,同位角相等”这一性质进行验证,再通过课件的演示对学生进行讲解,使学生加深对这一知识点的理解.
基于以上分析,确定本节课的教学重点为:掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补
二、目标和目标解析
1.目标
(1)掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;
(2)能够根据平行线的性质进行简单的推理.
2.目标解析
探索并掌握平行线的性质;能用平行线的性质定理进行简单的计算、证明;知道对平行线的性质和判定进行的区别;经历探索直线平行的性质的过程掌握平行线的三条性质,并能用它们进行简单的推理和计算;经历观察、操作、想像、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达能力;通过生活实际让学生自己发现问题、提出问题,然后进行建模解决问题;通过对平行线性质的探究,使学生初步认识数学与现实生活的密切联系;通过师生的共同活动,促使学生在学习活动中培养良好的情感、合作交流、主动参与的意识,在独立思考的同时能够认识他人.
三、教学问题诊断分析
在本节课学习之前,学生已经学行线的判定,了解到研究平行线与两条直线被第三条直线所截所形成的角,学生很自然地会想到研究平行线性质也要研究同位角、内错角、同旁内角的关系,所以本节课定理的学习,学生学起来会比较轻松.但独立思考和探究能力还有待培养和提高.从认知结构的角度看,学生已经具备一定的生活经验和数学活动经验,并且对基本几何图形有一定的认识.学生已经学了平行线的判定,具备了探究平行线性质的基础,但在逻辑思维和合作交流的意识方面发展不够均衡.重视学生的自主探究和合作交流以及创新意识的培养,充分利用七年级学生好奇、好强、好胜的心理特点,激发学生勇于探索和合作交流的学习气氛.
基于以上学情分析,确定本节课的教学难点为:平行线的判定和性质综合应用.
四、教学过程设计
复习回顾
根据右图,填空:
①如果∠1=∠C,
那么____∥____( )
② 如果∠1=∠B,
那么____∥____( )
③ 如果∠2+∠B=180°,
那么____∥____( )
问题:通过上题可知平行线的判定方法是什么?
思考:反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
合作探究
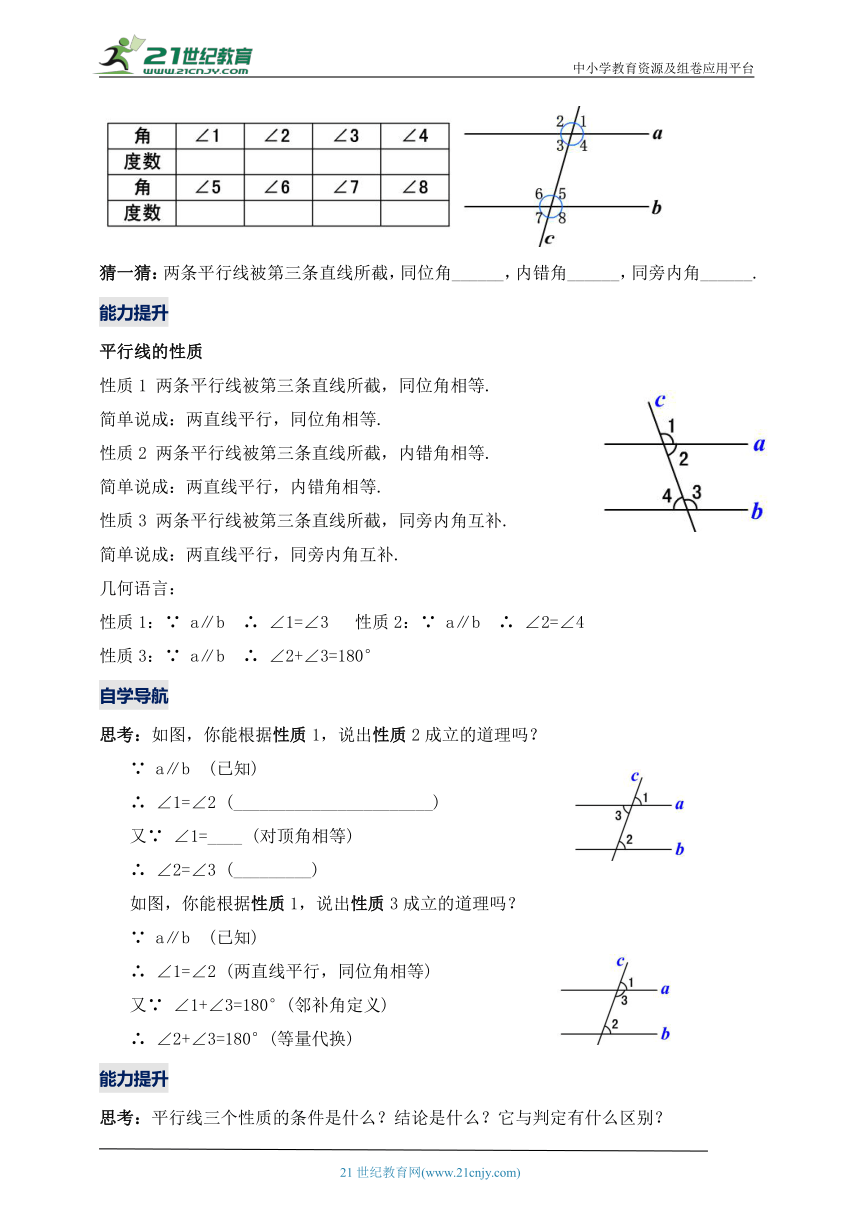
探究:利用坐标纸上的直线或者用直尺和三角尺画两条平行线a∥b,然后,画一条截线c与这两条平行线相交,度量所形成的8个角的度数,把结果填入下表:
猜一猜:两条平行线被第三条直线所截,同位角______,内错角______,同旁内角______.
能力提升
平行线的性质
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
几何语言:
性质1:∵ a∥b ∴ ∠1=∠3 性质2:∵ a∥b ∴ ∠2=∠4
性质3:∵ a∥b ∴ ∠2+∠3=180°
自学导航
思考:如图,你能根据性质1,说出性质2成立的道理吗?
∵ a∥b (已知)
∴ ∠1=∠2 (_______________________)
又∵ ∠1=____ (对顶角相等)
∴ ∠2=∠3 (_________)
如图,你能根据性质1,说出性质3成立的道理吗?
∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
又∵ ∠1+∠3=180°(邻补角定义)
∴ ∠2+∠3=180°(等量代换)
能力提升
思考:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?
考点解析
考点1:平行线的性质1
例1. 如图,D,E,F分别是三角形ABC三条边上的点,EF//AC,DF//AB,∠B=45°,∠C=60°.则∠EFD等于( )
A.80° B.75° C.70° D.65°
解析:
∵EF//AC,
∴∠EFB=∠C=60°(两直线平行,同位角相等)
∵ DF//AB,
∴∠DFC=∠B=45°(两直线平行,同位角相等)
∴∠EFD = 180°-∠EFB-∠DFC = 180°-60°-45°=75°.
【迁移应用】
1.如图,已知直线a//b,c为截线,若∠1=60°,则∠2的度数是( )
A.30° B.60° C.120° D.150°
2.如图,直线a//b,将一把三角尺的直角顶点放在直线b上,若∠1 =50°,则∠2的度数是( )
A.20° B.30° C.40° D.50°
3.如图,已知AB//CD,BC是∠ABD的平分线,若∠2= 64°,则∠3=______.
考点2:平行线的性质2
例2. 如图,已知AD//BC,∠B= 40°,∠DEC= 70°,求∠BDE的度数.
解:∵AD//BC,∠B=40°,∠DEC=70°
∴∠ADB=∠B= 40°,∠ADE=∠DEC=70°(两直线平行,内错角相等)
∴∠BDE=∠ADE-∠ADB=70°-40°=30°
【迁移应用】
1.如图,平行线AB,CD被直线EF所截,FG 平分∠EFD,若∠EFD=70°则 ∠EGF的度数是( )
A.35° B.55° C.70° D.110°
2.如图,直线a//b,点C,A分别在直线a,b上,AC⊥BC,若∠1=50°,则 ∠2的度数为______.
3.如图,AB//CD//EF,∠A=54°,∠C= 26°,则∠AFC=_______.
考点3:平行线的性质3
例3.如图,若AB//DE,BC//EF,求∠B+∠E的度数.
解:∵AB//DE (已知),
∴∠B=∠BCE(两直线平行,内错角相等 )
∵BC//EF(已知) ,
∴∠BCE+∠E=180°(两直线平行,同旁内角互补)
∴∠B+∠E=180°(等量代换)
【迁移应用】
1.如图,直线m//n,其中∠1= 40°,则∠2的度数为( )
A.130° B.140° C.150° D.160°
2.如图,直线a//b,直线c分别交a,b于点A,C,点B在直线b上,AB⊥AC.若∠1= 130,则∠2的度数是( )
A.30° B.40° C.50° D.70°
3.如图,已知AB//CD,∠1=∠2,∠EFD=56°,求∠D的度数.
解:∵AB//CD,∠EFD= 56°
∴∠BEF=180°- ∠EFD=124°
∵∠1= ∠2
∴∠2=∠BEF= 62°
∵AB//CD
∴∠D=∠2= 62°
考点4:利用平行线的性质解决折叠问题
例4. 如图,将一张长方形纸片(其中AD//BC)沿EF 折叠后,使得点A,B分别落在点A′B′的位置.若∠2=56°,求∠1的度数.
解:∵AD//BC,
∴∠B'FC=∠2= 56°( 两直线平行,同位角相等 )
由折叠的性质可知∠1=∠B′FE,
又∠1+∠B'FE+∠B′FC=180°
∴∠1=∠B'FE= (80°-∠B′FC)=×( 180°-56°)=62°.
【迁移应用】
1.如图,将一长方形纸片沿 AB 折叠,已知∠ABC=36°,则∠D1AD=( )
A.48° B.66° C.72° D.78°
2.如图,把一张对边平行的纸条沿EF折叠,点B,C分别落在点H,G处.若∠FEH=124°,则∠1=______.
3.如图,把一张长方形纸片ABCD沿EF折叠,点D,C 分别落在点D′,C′的位置上,ED′与BC 相交于点G.若∠EFG=55°,求∠1与∠2的度数.
解:∵∠EFG= 55°,AD //BC,
∴∠DEF =∠EFG =55°
由折叠的性质得∠DEG=2∠DEF=110°
∴∠1=180°-∠DEG=70°
∵AD//BC
∴∠2=∠DEG=110°
考点5:利用平行线的性质解决实际问题
例5. 一个大门栏杆的平面示意图如图所示,BA垂直于地面AE于点A,CD平行于地面AE.若∠BCD =10°则∠ABC=_______.
【解析】如图,过点B作BG//CD,
∴∠BCD+∠CBG=180°
∴∠CBG=180°-∠BCD=180°-150°=30°
∵BA⊥AE,
∴∠BAE=90°
∵CD//AE,BG//CD,
∴BG//AE
∴∠ABG+∠BAE= 180°
∴∠ABG= 180°-∠BAE= 90°
∴∠ABC=∠ABG+∠CBG=90°+30°=120°.
【迁移应用】
1.如图是超市购物车的侧面示意图,扶手AB与车底CD平行,∠1=100°, ∠2=48°,则∠3的度数是( )
A.52° B.48° C.42° D.62°
2. 如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM= 40°时,∠DCN的度数为(提示:由反射角=入射角,可得∠OBC =∠ABM,∠DCN=∠BCO)( )
A.40° B.50° C.60° D.80°
3.如图是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1, ∠2,则∠1+∠2=______.
考点6:平行线的判定和性质的综合应用
例6. 如图,已知CE⊥AB,MN⊥AB,∠EDC+∠ACB=180°.试说明:∠1=∠2.
解:∵CE⊥AB,MN⊥AB,
∴∠CEB=∠MNB=90°,
∴MN//CE,
∴∠2=∠BCE.
∵∠EDC+∠ACB=180°,
∴ED//BC,
∴∠1=∠BCE,
∴∠1=∠2.
例7. 如图,点F在线段AB上,点E,G在线段CD上,AB//CD.
(1)若BC平分∠ABD,∠D=100°,求∠ABC的度数;
(2)若∠1=∠2,试说明:AE∥FG.
解:(1)∵AB//CD,
∴∠ABD+∠D=180°
∵∠D=100°,
∴∠ABD=180°-∠D=80°.
∵BC平分∠ABD
∴∠ABC=∠ABD=40°
(2)∵AB//CD
∴∠1=∠FGC.
又∠1=∠2
∴∠FCC=∠2
∴AE// FG.
【迁移应用】
1.如图,点Р在直线CD上,∠BAP+∠APD=180°,∠1=∠2.试说明:∠E=∠F.
解:∠BAP+∠APD=180°,
∴AB//CD,
∴∠BAP =∠APC.
又∠1=∠2,∠3=∠BAP-∠1, ∠4=∠APC-∠2,
∴∠3=∠4,
∴AE//PF,
∴∠E=∠F.
2.如图,AB//CD,点F在CD上,延长BC,AF交于点E,∠1=∠2,∠3 =∠4.试说明:AD//BE.
解:∵AB//CD,
∴∠4=∠BAE
∵∠3=∠4
∴ ∠3=∠BAE
∵∠1=∠2
∴ ∠1+∠CAE =∠2+∠CAE,即∠BAE=∠CAD,
∴∠3=∠CAD
∴AD//BE.
3.如图,∠1+∠2=180°.
(1)试说明:AB∥EF;
(2)若CD平分∠ACB,∠DEF=∠A,∠BED=60°,求∠EDF的度数.
解:(1) ∵∠1与∠EFD是邻补角,
∴∠1+∠EFD= 180°
又∠1+∠2=180°
∴∠2=∠EFD
∴AB//EF.
(2)∵AB//EF ,
∴∠DEF=∠BDE.
又∠DEF=∠A
∴∠A=∠BDE
∴DE//AC
∴∠ACB=∠BED=60°
∵CD平分∠ ACB
∴∠ACD=∠ACB=30°
∵DE//AC
∴∠EDF=∠ACD=30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.3.1 平行线的性质 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第五章“相交线与平行线” 5.3.1平行线的性质,内容包括:平行线的性质;平行线的判定和性质综合应用.
2.内容解析
《平行线的性质》人教版七年级数学下册的内容,本节课是在学生已经学习了同位角、内错角、同旁内角和平行线的判定的基础上进行教学的.这节课是空间与图形领域的基础知识,在以后的学习中经常要用到.它为今后三角形内角和、三角形全等、三角形相似等知识的学习奠定了理论基础,学好这部分内容至关重要。在这节课的学习中,我先组织学生利用手中的量角器对“两直线平行,同位角相等”这一性质进行验证,再通过课件的演示对学生进行讲解,使学生加深对这一知识点的理解.
基于以上分析,确定本节课的教学重点为:掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补
二、目标和目标解析
1.目标
(1)掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;
(2)能够根据平行线的性质进行简单的推理.
2.目标解析
探索并掌握平行线的性质;能用平行线的性质定理进行简单的计算、证明;知道对平行线的性质和判定进行的区别;经历探索直线平行的性质的过程掌握平行线的三条性质,并能用它们进行简单的推理和计算;经历观察、操作、想像、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达能力;通过生活实际让学生自己发现问题、提出问题,然后进行建模解决问题;通过对平行线性质的探究,使学生初步认识数学与现实生活的密切联系;通过师生的共同活动,促使学生在学习活动中培养良好的情感、合作交流、主动参与的意识,在独立思考的同时能够认识他人.
三、教学问题诊断分析
在本节课学习之前,学生已经学行线的判定,了解到研究平行线与两条直线被第三条直线所截所形成的角,学生很自然地会想到研究平行线性质也要研究同位角、内错角、同旁内角的关系,所以本节课定理的学习,学生学起来会比较轻松.但独立思考和探究能力还有待培养和提高.从认知结构的角度看,学生已经具备一定的生活经验和数学活动经验,并且对基本几何图形有一定的认识.学生已经学了平行线的判定,具备了探究平行线性质的基础,但在逻辑思维和合作交流的意识方面发展不够均衡.重视学生的自主探究和合作交流以及创新意识的培养,充分利用七年级学生好奇、好强、好胜的心理特点,激发学生勇于探索和合作交流的学习气氛.
基于以上学情分析,确定本节课的教学难点为:平行线的判定和性质综合应用.
四、教学过程设计
复习回顾
根据右图,填空:
①如果∠1=∠C,
那么____∥____( )
② 如果∠1=∠B,
那么____∥____( )
③ 如果∠2+∠B=180°,
那么____∥____( )
问题:通过上题可知平行线的判定方法是什么?
思考:反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
合作探究
探究:利用坐标纸上的直线或者用直尺和三角尺画两条平行线a∥b,然后,画一条截线c与这两条平行线相交,度量所形成的8个角的度数,把结果填入下表:
猜一猜:两条平行线被第三条直线所截,同位角______,内错角______,同旁内角______.
能力提升
平行线的性质
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
几何语言:
性质1:∵ a∥b ∴ ∠1=∠3 性质2:∵ a∥b ∴ ∠2=∠4
性质3:∵ a∥b ∴ ∠2+∠3=180°
自学导航
思考:如图,你能根据性质1,说出性质2成立的道理吗?
∵ a∥b (已知)
∴ ∠1=∠2 (_______________________)
又∵ ∠1=____ (对顶角相等)
∴ ∠2=∠3 (_________)
如图,你能根据性质1,说出性质3成立的道理吗?
∵ a∥b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
又∵ ∠1+∠3=180°(邻补角定义)
∴ ∠2+∠3=180°(等量代换)
能力提升
思考:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?
考点解析
考点1:平行线的性质1
例1. 如图,D,E,F分别是三角形ABC三条边上的点,EF//AC,DF//AB,∠B=45°,∠C=60°.则∠EFD等于( )
A.80° B.75° C.70° D.65°
解析:
∵EF//AC,
∴∠EFB=∠C=60°(两直线平行,同位角相等)
∵ DF//AB,
∴∠DFC=∠B=45°(两直线平行,同位角相等)
∴∠EFD = 180°-∠EFB-∠DFC = 180°-60°-45°=75°.
【迁移应用】
1.如图,已知直线a//b,c为截线,若∠1=60°,则∠2的度数是( )
A.30° B.60° C.120° D.150°
2.如图,直线a//b,将一把三角尺的直角顶点放在直线b上,若∠1 =50°,则∠2的度数是( )
A.20° B.30° C.40° D.50°
3.如图,已知AB//CD,BC是∠ABD的平分线,若∠2= 64°,则∠3=______.
考点2:平行线的性质2
例2. 如图,已知AD//BC,∠B= 40°,∠DEC= 70°,求∠BDE的度数.
解:∵AD//BC,∠B=40°,∠DEC=70°
∴∠ADB=∠B= 40°,∠ADE=∠DEC=70°(两直线平行,内错角相等)
∴∠BDE=∠ADE-∠ADB=70°-40°=30°
【迁移应用】
1.如图,平行线AB,CD被直线EF所截,FG 平分∠EFD,若∠EFD=70°则 ∠EGF的度数是( )
A.35° B.55° C.70° D.110°
2.如图,直线a//b,点C,A分别在直线a,b上,AC⊥BC,若∠1=50°,则 ∠2的度数为______.
3.如图,AB//CD//EF,∠A=54°,∠C= 26°,则∠AFC=_______.
考点3:平行线的性质3
例3.如图,若AB//DE,BC//EF,求∠B+∠E的度数.
解:∵AB//DE (已知),
∴∠B=∠BCE(两直线平行,内错角相等 )
∵BC//EF(已知) ,
∴∠BCE+∠E=180°(两直线平行,同旁内角互补)
∴∠B+∠E=180°(等量代换)
【迁移应用】
1.如图,直线m//n,其中∠1= 40°,则∠2的度数为( )
A.130° B.140° C.150° D.160°
2.如图,直线a//b,直线c分别交a,b于点A,C,点B在直线b上,AB⊥AC.若∠1= 130,则∠2的度数是( )
A.30° B.40° C.50° D.70°
3.如图,已知AB//CD,∠1=∠2,∠EFD=56°,求∠D的度数.
解:∵AB//CD,∠EFD= 56°
∴∠BEF=180°- ∠EFD=124°
∵∠1= ∠2
∴∠2=∠BEF= 62°
∵AB//CD
∴∠D=∠2= 62°
考点4:利用平行线的性质解决折叠问题
例4. 如图,将一张长方形纸片(其中AD//BC)沿EF 折叠后,使得点A,B分别落在点A′B′的位置.若∠2=56°,求∠1的度数.
解:∵AD//BC,
∴∠B'FC=∠2= 56°( 两直线平行,同位角相等 )
由折叠的性质可知∠1=∠B′FE,
又∠1+∠B'FE+∠B′FC=180°
∴∠1=∠B'FE= (80°-∠B′FC)=×( 180°-56°)=62°.
【迁移应用】
1.如图,将一长方形纸片沿 AB 折叠,已知∠ABC=36°,则∠D1AD=( )
A.48° B.66° C.72° D.78°
2.如图,把一张对边平行的纸条沿EF折叠,点B,C分别落在点H,G处.若∠FEH=124°,则∠1=______.
3.如图,把一张长方形纸片ABCD沿EF折叠,点D,C 分别落在点D′,C′的位置上,ED′与BC 相交于点G.若∠EFG=55°,求∠1与∠2的度数.
解:∵∠EFG= 55°,AD //BC,
∴∠DEF =∠EFG =55°
由折叠的性质得∠DEG=2∠DEF=110°
∴∠1=180°-∠DEG=70°
∵AD//BC
∴∠2=∠DEG=110°
考点5:利用平行线的性质解决实际问题
例5. 一个大门栏杆的平面示意图如图所示,BA垂直于地面AE于点A,CD平行于地面AE.若∠BCD =10°则∠ABC=_______.
【解析】如图,过点B作BG//CD,
∴∠BCD+∠CBG=180°
∴∠CBG=180°-∠BCD=180°-150°=30°
∵BA⊥AE,
∴∠BAE=90°
∵CD//AE,BG//CD,
∴BG//AE
∴∠ABG+∠BAE= 180°
∴∠ABG= 180°-∠BAE= 90°
∴∠ABC=∠ABG+∠CBG=90°+30°=120°.
【迁移应用】
1.如图是超市购物车的侧面示意图,扶手AB与车底CD平行,∠1=100°, ∠2=48°,则∠3的度数是( )
A.52° B.48° C.42° D.62°
2. 如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM= 40°时,∠DCN的度数为(提示:由反射角=入射角,可得∠OBC =∠ABM,∠DCN=∠BCO)( )
A.40° B.50° C.60° D.80°
3.如图是我们生活中经常接触的小刀,刀柄是一个直角梯形(挖去一个半圆),刀片上下是平行的,转动刀片时会形成∠1, ∠2,则∠1+∠2=______.
考点6:平行线的判定和性质的综合应用
例6. 如图,已知CE⊥AB,MN⊥AB,∠EDC+∠ACB=180°.试说明:∠1=∠2.
解:∵CE⊥AB,MN⊥AB,
∴∠CEB=∠MNB=90°,
∴MN//CE,
∴∠2=∠BCE.
∵∠EDC+∠ACB=180°,
∴ED//BC,
∴∠1=∠BCE,
∴∠1=∠2.
例7. 如图,点F在线段AB上,点E,G在线段CD上,AB//CD.
(1)若BC平分∠ABD,∠D=100°,求∠ABC的度数;
(2)若∠1=∠2,试说明:AE∥FG.
解:(1)∵AB//CD,
∴∠ABD+∠D=180°
∵∠D=100°,
∴∠ABD=180°-∠D=80°.
∵BC平分∠ABD
∴∠ABC=∠ABD=40°
(2)∵AB//CD
∴∠1=∠FGC.
又∠1=∠2
∴∠FCC=∠2
∴AE// FG.
【迁移应用】
1.如图,点Р在直线CD上,∠BAP+∠APD=180°,∠1=∠2.试说明:∠E=∠F.
解:∠BAP+∠APD=180°,
∴AB//CD,
∴∠BAP =∠APC.
又∠1=∠2,∠3=∠BAP-∠1, ∠4=∠APC-∠2,
∴∠3=∠4,
∴AE//PF,
∴∠E=∠F.
2.如图,AB//CD,点F在CD上,延长BC,AF交于点E,∠1=∠2,∠3 =∠4.试说明:AD//BE.
解:∵AB//CD,
∴∠4=∠BAE
∵∠3=∠4
∴ ∠3=∠BAE
∵∠1=∠2
∴ ∠1+∠CAE =∠2+∠CAE,即∠BAE=∠CAD,
∴∠3=∠CAD
∴AD//BE.
3.如图,∠1+∠2=180°.
(1)试说明:AB∥EF;
(2)若CD平分∠ACB,∠DEF=∠A,∠BED=60°,求∠EDF的度数.
解:(1) ∵∠1与∠EFD是邻补角,
∴∠1+∠EFD= 180°
又∠1+∠2=180°
∴∠2=∠EFD
∴AB//EF.
(2)∵AB//EF ,
∴∠DEF=∠BDE.
又∠DEF=∠A
∴∠A=∠BDE
∴DE//AC
∴∠ACB=∠BED=60°
∵CD平分∠ ACB
∴∠ACD=∠ACB=30°
∵DE//AC
∴∠EDF=∠ACD=30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
