【2024春人教七下数学精品教案】6_1_3 平方根(第三课时) 教案
文档属性
| 名称 | 【2024春人教七下数学精品教案】6_1_3 平方根(第三课时) 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 13:22:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
6.1.3 平方根 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第六章“实数”6.1.3 平方根,内容包括:平方根的概念、理解平方与开平方的关系、会求非负数的平方根.
2.内容解析
平方根及其相关概念是在学生已经掌握了有理数、有理数的乘方、用字母表示数等知识的基础上,正式进入实数知识学习的起始内容.在介绍平方根及其相关概念的同时,将首次出现用根号形式表示的无理数,以及无限不循环小数,并引入开平方运算等.这些知识是对前面所学知识的深化和发展,其中有的知识是学习实数、二次根式的预备知识,有的知识是用直接开平方法、公式法解一元二次方程的重要依据.因此,平方根的学习处于非常重要的地位,起着承前启后的作用.
基于以上分析,确定本节课的教学重点为:了解平方根的概念和开平方的概念,掌握平方根的特征;会求非负数的平方根.
二、目标和目标解析
1.目标
(1)了解平方根的概念和开平方的概念,掌握平方根的特征.
(2)能利用开平方与平方互为逆运算的关系,会求非负数的平方根.
(3)能正确区分算术平方根与平方根.
2.目标解析
学生了解如果一个数的平方根等于a,那么这个数叫a的平方根或二次方根,并会归纳出平方根的特征.即正数的平方根有两个,它们互为相反数,0的平方根是0,负数没有平方根.学生知道开平方运算与平方运算互为逆运算,给一个非负数a,能找出所有满足x2=a的x.学生知道怎样表示一个非负数的平方根与算术平方根,会正确读出并理解一个非负数的平方根与算术平方根的意义.
三、教学问题诊断分析
学生对于平方根与算术平方根的概念容易混淆,经常出现“=±2”的错误.在刚开始接触平方根时,可能还有两点不太习惯,一是正数有两个平方根,即正数进行开平方运算有两个结果,这与过去学生遇到的运算结果唯一的情况有所不同;二是负数没有平方根,即负数不能进行开平方运算,这种对运算对象有限定要求的情况以前一般不会遇到.
基于以上学情分析,确定本节课的教学难点为:平方根与算术平方根的区别与联系.
四、教学过程设计
复习回顾
1.什么叫一个数的算术平方根?怎样表示?
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.
a的算术平方根表示为:(a≥0),0的算术平方根是0,负数没有算术平方根.
2.25的算术平方根是_____,13的算术平方根是_____.
自学导航
思考:如果一个数的平方等于9,这个数是多少?由于(±3)2=9,所以这个数是3或-3.
3是前面学习过的9的算术平方根,-3与9的算术平方根有什么关系?(与算术平方根互为相反数.)
归纳平方根的概念
填表:
如果我们把±1,±4,±6,±7,±分别叫做1,16,36,49,的平方根,你能类比算术平方根的概念,给出平方根的概念吗?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根. 这就是说,如果x2=a,那么x叫做a的平方根.
例如,3和-3是9的平方根,简记为±3是9的平方根.
求一个数a的平方根的运算,叫做开平方.
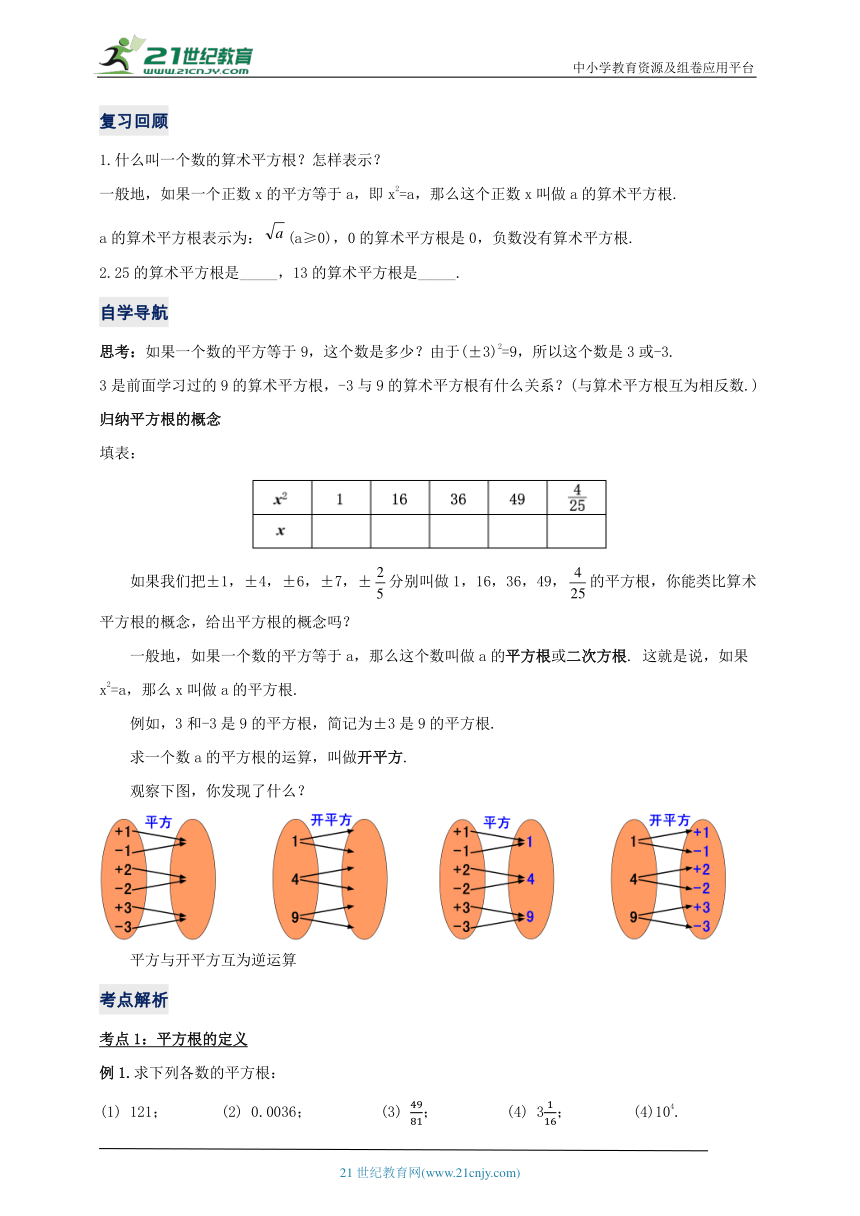
观察下图,你发现了什么?
平方与开平方互为逆运算
考点解析
考点1:平方根的定义
例1.求下列各数的平方根:
(1) 121; (2) 0.0036; (3) ; (4) 3; (4)104.
解:(1)因为(±11)2=121,所以121的平方根是±11;
(2)因为(±0.06)2=0.0036,所以0.0036的平方根是±0.06;
(3)因为 = ,所以的平方根是±;
(4)因为3==,所以3的平方根是±;
(5)因为104=10000,(±100)2=10000,所以104的平方根是±11;
【迁移应用】
1.4的平方根是( )
A.2 B.-2 C.+2 D.16
2.“36的平方根是±6”用数学式子表示正确的是( )
A.=6 B.=6 C. =±6 D. =±6
3.下列说法正确的是( )
A.10的平方根是100 B.100的平方根是10
C.100的平方根是-10 D.100的平方根是±10
4.的平方根是______.
5.求下列各数的平方根:
(1) 64; (2) 0.0025; (3) ; (4)(-4)2; (4)5.
解:(1)因为(±8)2=64,所以64的平方根是±8;
(2)因为(±0.05)2=0.0025,所以0.0025的平方根是±0.05;
(3)因为 = ,所以的平方根是;
(4)因为(-4)2=16,(±4)2=16,所以(-4)2的平方根是±4;
(5)因为5==,所以3的平方根是±;
能力提升
数的平方根的特征:
1.正数的平方根有什么特点?(正数有两个平方根,它们互为相反数)
2.0的平方根是多少?(0的平方根是0)
3.负数有平方根吗?(负数没有平方根)
平方根的表示
我们已经学过一个正数的算术平方根的表示方法,你能表示一个正数的平方根吗?
正数a的算术平方根可以表示为,正数a的负的平方根,可以表示为-.
正数a的平方根可以用±表示,读作“正、负根号a”.
例如,±=±3,±=±5.
平方根与算术平方根的联系与区别:
考点解析
考点2:平方根的性质
例2.已知一个正数的两个平方根分别是2a-1和a-5,求这个正数.
解:根据题意,得(2a-1)+(a-5)=0,解得a=2.
所以2a-1=3,32=9,所以这个正数为9.
【迁移应用】
1.若数a-2有平方根,则a可以取( )
A.-1 B.0 C.1 D.2
2.平方根等于它自己的数是( )
A.0 B.1 C.-1 D.4
3.已知a-1与3-2a是某正数的两个平方根,则数a的值是_____.
4.如果3x-2和5x+6都是一个非负数的平方根,那么这个数是__________.
考点3:算术平方根与平方根的关系
例3.求下列各式的值:
(1); (2)-; (3)±.
解:(1)因为192=361,所以=19;
(2)因为12.25=,=,所以-=-;
(3)因为4=,=,所以±=±.
【迁移应用】
1.下列叙述中正确的是( )
A.-3是9的平方根 B.9的平方根是-3
C.-3是(-3)2的算术平方根 D.±3是(-3)2的算术平方根
2.下列计算错误的是( )
A. =±2 B. =3 C.± =±4 D.-=-5
3.144的算术平方根是_____,平方根是_____.
4.已知正数a的算术平方根为,则a的平方根是______,a=_____.
5.求下列各式的值:
(1)-; (2) (3)±; (4).
解:(1)-=-9; (2) (3)±=±1.5; (4)=7.
考点4:平方根与算术平方根的综合应用
例4. 已知2a+1的平方根是±3,5a+2b-2的算术平方根是4,求3a-4b的平方根.
解:依题意,得2a+1=(±3)2=9,可得a=4.
所以5a+2b-2=5×4+2b-2=2b+18.
所以2b+18=42=16,可得b=-1.
所以3a-4b=3×4-4×(-1)=16.
因为(±4)2=16,
所以3a-4b的平方根是±4.
【迁移应用】
1.一个自然数的算术平方根是a,则与它相邻的下一个自然数的平方根是( )
A.± B.a+1 C.a2+1 D.±
2.若2x+1的平方根是±5,则5x+4的算术平方根是_____.
3.一个数的算术平方根为2a-6,平方根为±(a-1),求a的值与这个数.
解:分两种情况:①当2a-6=a-1时,可得a=5,此时2a-6=4,42=16;
②当2a-6=-(a-1)时,可得a=,此时2a-6=-,不符合题意,此种情况不存在.
所以a的值为5,这个数为16.
考点5:利用平方根解形如x2=a(a≥0)的方程
例5.求下列各式中x的值:
(1)3x2=48; (2) (x+1)2=4; (3)2(x-1)2-18=0.
解:(1)原式可变形为x2=16.
因为(±4)2= 16,
所以x=4或x=-4.
(2)因为(±2)2=4,
所以x+1=2或x+1=-2,
解方程,得x=1或x=-3.
所以x=1或x=-3.
(3)原式可变形为(x-1)2=9.
因为(±3)2=9,
所以x-1=3或x-1=-3
解方程,得x=4或x=-2.
所以x=4或x=-2.
【迁移应用】
求下列各式中x的值:
(1)4x2-1=0; (2) (x+1)2=81; (3)9(x-1)2=4; (4)(2x-3)2-64=0.
解:(1)原式可变形为x2= ,
因为(±)2=,
所以x=或x=-.
(2)因为(±9)2=81,
所以x+1=9或x+1=-9,
解方程,得x=8或x=-10.
所以x=8或x=-10.
(3) 原式可变形为(x-1)2=.
因为(±)2=.
所以x-1=或x-1=-.
解方程,得x=或x=.
所以x=或x=.
(4)原式可变形为(2x-3)2= 64.
因为(±8)2=64,
所以2x-3=8或2x-3=-8.
解方程,得x=或x=-.
所以x=或x=-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.1.3 平方根 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第六章“实数”6.1.3 平方根,内容包括:平方根的概念、理解平方与开平方的关系、会求非负数的平方根.
2.内容解析
平方根及其相关概念是在学生已经掌握了有理数、有理数的乘方、用字母表示数等知识的基础上,正式进入实数知识学习的起始内容.在介绍平方根及其相关概念的同时,将首次出现用根号形式表示的无理数,以及无限不循环小数,并引入开平方运算等.这些知识是对前面所学知识的深化和发展,其中有的知识是学习实数、二次根式的预备知识,有的知识是用直接开平方法、公式法解一元二次方程的重要依据.因此,平方根的学习处于非常重要的地位,起着承前启后的作用.
基于以上分析,确定本节课的教学重点为:了解平方根的概念和开平方的概念,掌握平方根的特征;会求非负数的平方根.
二、目标和目标解析
1.目标
(1)了解平方根的概念和开平方的概念,掌握平方根的特征.
(2)能利用开平方与平方互为逆运算的关系,会求非负数的平方根.
(3)能正确区分算术平方根与平方根.
2.目标解析
学生了解如果一个数的平方根等于a,那么这个数叫a的平方根或二次方根,并会归纳出平方根的特征.即正数的平方根有两个,它们互为相反数,0的平方根是0,负数没有平方根.学生知道开平方运算与平方运算互为逆运算,给一个非负数a,能找出所有满足x2=a的x.学生知道怎样表示一个非负数的平方根与算术平方根,会正确读出并理解一个非负数的平方根与算术平方根的意义.
三、教学问题诊断分析
学生对于平方根与算术平方根的概念容易混淆,经常出现“=±2”的错误.在刚开始接触平方根时,可能还有两点不太习惯,一是正数有两个平方根,即正数进行开平方运算有两个结果,这与过去学生遇到的运算结果唯一的情况有所不同;二是负数没有平方根,即负数不能进行开平方运算,这种对运算对象有限定要求的情况以前一般不会遇到.
基于以上学情分析,确定本节课的教学难点为:平方根与算术平方根的区别与联系.
四、教学过程设计
复习回顾
1.什么叫一个数的算术平方根?怎样表示?
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.
a的算术平方根表示为:(a≥0),0的算术平方根是0,负数没有算术平方根.
2.25的算术平方根是_____,13的算术平方根是_____.
自学导航
思考:如果一个数的平方等于9,这个数是多少?由于(±3)2=9,所以这个数是3或-3.
3是前面学习过的9的算术平方根,-3与9的算术平方根有什么关系?(与算术平方根互为相反数.)
归纳平方根的概念
填表:
如果我们把±1,±4,±6,±7,±分别叫做1,16,36,49,的平方根,你能类比算术平方根的概念,给出平方根的概念吗?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根. 这就是说,如果x2=a,那么x叫做a的平方根.
例如,3和-3是9的平方根,简记为±3是9的平方根.
求一个数a的平方根的运算,叫做开平方.
观察下图,你发现了什么?
平方与开平方互为逆运算
考点解析
考点1:平方根的定义
例1.求下列各数的平方根:
(1) 121; (2) 0.0036; (3) ; (4) 3; (4)104.
解:(1)因为(±11)2=121,所以121的平方根是±11;
(2)因为(±0.06)2=0.0036,所以0.0036的平方根是±0.06;
(3)因为 = ,所以的平方根是±;
(4)因为3==,所以3的平方根是±;
(5)因为104=10000,(±100)2=10000,所以104的平方根是±11;
【迁移应用】
1.4的平方根是( )
A.2 B.-2 C.+2 D.16
2.“36的平方根是±6”用数学式子表示正确的是( )
A.=6 B.=6 C. =±6 D. =±6
3.下列说法正确的是( )
A.10的平方根是100 B.100的平方根是10
C.100的平方根是-10 D.100的平方根是±10
4.的平方根是______.
5.求下列各数的平方根:
(1) 64; (2) 0.0025; (3) ; (4)(-4)2; (4)5.
解:(1)因为(±8)2=64,所以64的平方根是±8;
(2)因为(±0.05)2=0.0025,所以0.0025的平方根是±0.05;
(3)因为 = ,所以的平方根是;
(4)因为(-4)2=16,(±4)2=16,所以(-4)2的平方根是±4;
(5)因为5==,所以3的平方根是±;
能力提升
数的平方根的特征:
1.正数的平方根有什么特点?(正数有两个平方根,它们互为相反数)
2.0的平方根是多少?(0的平方根是0)
3.负数有平方根吗?(负数没有平方根)
平方根的表示
我们已经学过一个正数的算术平方根的表示方法,你能表示一个正数的平方根吗?
正数a的算术平方根可以表示为,正数a的负的平方根,可以表示为-.
正数a的平方根可以用±表示,读作“正、负根号a”.
例如,±=±3,±=±5.
平方根与算术平方根的联系与区别:
考点解析
考点2:平方根的性质
例2.已知一个正数的两个平方根分别是2a-1和a-5,求这个正数.
解:根据题意,得(2a-1)+(a-5)=0,解得a=2.
所以2a-1=3,32=9,所以这个正数为9.
【迁移应用】
1.若数a-2有平方根,则a可以取( )
A.-1 B.0 C.1 D.2
2.平方根等于它自己的数是( )
A.0 B.1 C.-1 D.4
3.已知a-1与3-2a是某正数的两个平方根,则数a的值是_____.
4.如果3x-2和5x+6都是一个非负数的平方根,那么这个数是__________.
考点3:算术平方根与平方根的关系
例3.求下列各式的值:
(1); (2)-; (3)±.
解:(1)因为192=361,所以=19;
(2)因为12.25=,=,所以-=-;
(3)因为4=,=,所以±=±.
【迁移应用】
1.下列叙述中正确的是( )
A.-3是9的平方根 B.9的平方根是-3
C.-3是(-3)2的算术平方根 D.±3是(-3)2的算术平方根
2.下列计算错误的是( )
A. =±2 B. =3 C.± =±4 D.-=-5
3.144的算术平方根是_____,平方根是_____.
4.已知正数a的算术平方根为,则a的平方根是______,a=_____.
5.求下列各式的值:
(1)-; (2) (3)±; (4).
解:(1)-=-9; (2) (3)±=±1.5; (4)=7.
考点4:平方根与算术平方根的综合应用
例4. 已知2a+1的平方根是±3,5a+2b-2的算术平方根是4,求3a-4b的平方根.
解:依题意,得2a+1=(±3)2=9,可得a=4.
所以5a+2b-2=5×4+2b-2=2b+18.
所以2b+18=42=16,可得b=-1.
所以3a-4b=3×4-4×(-1)=16.
因为(±4)2=16,
所以3a-4b的平方根是±4.
【迁移应用】
1.一个自然数的算术平方根是a,则与它相邻的下一个自然数的平方根是( )
A.± B.a+1 C.a2+1 D.±
2.若2x+1的平方根是±5,则5x+4的算术平方根是_____.
3.一个数的算术平方根为2a-6,平方根为±(a-1),求a的值与这个数.
解:分两种情况:①当2a-6=a-1时,可得a=5,此时2a-6=4,42=16;
②当2a-6=-(a-1)时,可得a=,此时2a-6=-,不符合题意,此种情况不存在.
所以a的值为5,这个数为16.
考点5:利用平方根解形如x2=a(a≥0)的方程
例5.求下列各式中x的值:
(1)3x2=48; (2) (x+1)2=4; (3)2(x-1)2-18=0.
解:(1)原式可变形为x2=16.
因为(±4)2= 16,
所以x=4或x=-4.
(2)因为(±2)2=4,
所以x+1=2或x+1=-2,
解方程,得x=1或x=-3.
所以x=1或x=-3.
(3)原式可变形为(x-1)2=9.
因为(±3)2=9,
所以x-1=3或x-1=-3
解方程,得x=4或x=-2.
所以x=4或x=-2.
【迁移应用】
求下列各式中x的值:
(1)4x2-1=0; (2) (x+1)2=81; (3)9(x-1)2=4; (4)(2x-3)2-64=0.
解:(1)原式可变形为x2= ,
因为(±)2=,
所以x=或x=-.
(2)因为(±9)2=81,
所以x+1=9或x+1=-9,
解方程,得x=8或x=-10.
所以x=8或x=-10.
(3) 原式可变形为(x-1)2=.
因为(±)2=.
所以x-1=或x-1=-.
解方程,得x=或x=.
所以x=或x=.
(4)原式可变形为(2x-3)2= 64.
因为(±8)2=64,
所以2x-3=8或2x-3=-8.
解方程,得x=或x=-.
所以x=或x=-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
