六年级数学下册人教版5.2 鸽巢问题的一般形式课件(共23张PPT)
文档属性
| 名称 | 六年级数学下册人教版5.2 鸽巢问题的一般形式课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 19:43:51 | ||
图片预览



文档简介
(共23张PPT)
鸽巢问题的一般形式
第五单元 数学广角——鸽巢问题
鸽巢原理
谁能说一说上节课我们学习了什么?
(n+1) 只鸽子飞进n个鸽巢里,(n是非0自然数),总有1个鸽巢里至少飞进2只鸽子。
这种原理叫作鸽巢原理,也叫抽屉原理。
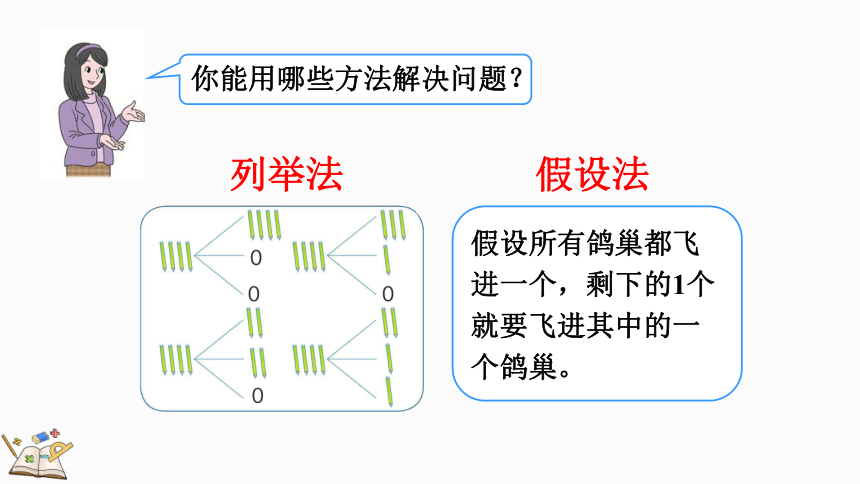
列举法
你能用哪些方法解决问题?
假设所有鸽巢都飞进一个,剩下的1个就要飞进其中的一个鸽巢。
假设法
2
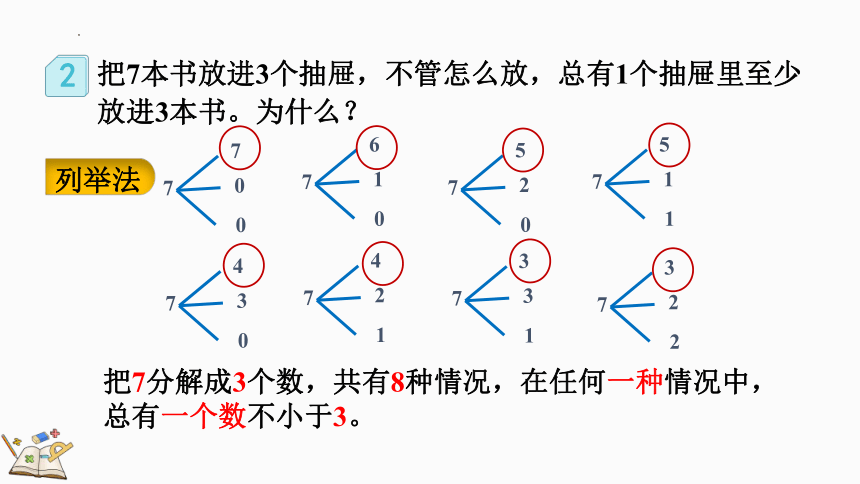
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
想一想,你能怎样放呢?
如果每个抽屉最多放2本,那么3个抽屉最多放6本,可题目要求放的是7本书。所以……
我随便放放看,
一个抽屉1本,
一个抽屉2本,
一个抽屉4本。
把7本书分成3份,尽量平均分,多出的1本总要放进其中1个抽屉里。
2
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
与同伴实践操作一下验证你的想法吧!
2
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
7
7
0
0
列举法
7
6
1
0
7
5
2
0
7
5
1
1
7
4
3
0
7
4
2
1
7
3
3
1
7
3
2
2
把7分解成3个数,共有8种情况,在任何一种情况中,总有一个数不小于3。
2
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
7÷3=2(本)……1(本)
余下的一本放在哪个抽屉都导致“总有一个抽屉至少有3本书”。
假设法
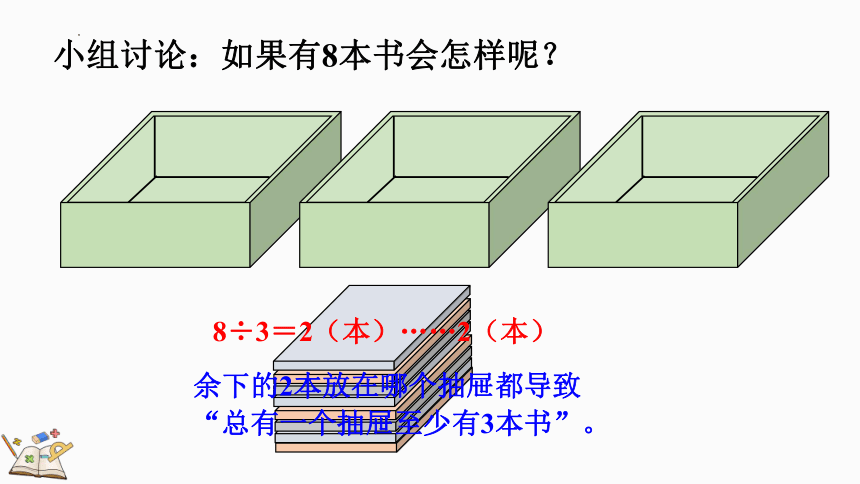
小组讨论:如果有8本书会怎样呢?
8÷3=2(本)……2(本)
余下的2本放在哪个抽屉都导致“总有一个抽屉至少有3本书”。
如果有9本书会怎样呢?
9÷3=3(本)
有10本书呢?
10÷3=3(本)……1(本)
余下的一本放在哪个抽屉都导致“总有一个抽屉至少有4本书”。
7 ÷ 3 = 2(本)…… 1(本)
8 ÷ 3 = 2 (本)…… 2(本)
10 ÷ 3 = 3 (本)…… 1(本)
总本数
抽屉数
平均每个抽屉放进的本数
剩下的本数
物体数
剩下1本,任选其中一个抽屉放进去。
剩下2本,任选其中1个或2个抽屉放进去。
整理这些算式,你发现了什么?
7÷3 = 2(本)…… 1(本)
8÷3 = 2(本)…… 2(本)
10÷3 = 3(本)…… 1(本)
3 + 1=4(本)
2 + 1=3(本)
2 + 1= 3(本)
抽屉数
物体数
商
余数
商+1
至少数
余数不论是多少,都加1。
如果物体数除以抽屉数有余数,用所得的商加1,就会发现“总有一个抽屉里至少有商加1个物体”。
至少数=商+1
整理这些算式,你发现了什么?
(kn+a)÷n=k……a
把(kn+a)(a计算法
8÷3=2(本)…… 2(本)
10÷3=3(本)…… 1(本)
答:把8本书放进3个抽屉里,总有一个抽屉至少放进3本书。
答:把10本书放进3个抽屉里,总有一个抽屉至少放进4本书。
至少数=商+1
2+1=3(本)
3+1=4(本)
如果有8本书会怎样呢?
10本呢?
选自教材第68页做一做第1题
1
11÷4 = 2(只)……3(只)
2 + 1 = 3(只)
11只鸽子飞进了4个鸽笼,总有1个鸽笼至少飞进了3只鸽子。为什么?
余下的3只,不论怎么飞,总有
1个鸽笼里至少再飞进1只鸽子。
选自教材第68页做一做第2题
2
色一定和前8人中的2人重复。
假设前8人每2人拿的花色一样,
那么第9个人拿的牌花
所以至少有3张牌是相
小明表演扑克牌“魔术”。一副扑克牌,取出大小王,还剩52张牌,9人每人随意抽1张,至少有3张牌是相同的花色。你理解这个扑克牌“魔术”的道理吗?
52张扑克牌里只有黑桃、红桃、梅花、方片4种花色。
9÷4 = 2(张)……1(张)
同的花色。
2 + 1 = 3(张)
1.把鸽子放进对应的笼子中,完成下表:
鸽子只数 笼子的个数 结果
6 5
总有一个笼子里至少放进( )
只鸽子。
7 6
10 9
100 99
2
只要放的鸽子数比笼子的数量多1,那么总有一个笼子里至少放进2只鸽子。
2.六年级三班,有50人,每人至少订一份学习刊物,现有A、B、C三种刊物,每人有几种选择方式?这个班订相同刊物的至少有多少人?
把有几种选择方式,看作抽屉数。
①A ②B ③C ④A和B ⑤A和C ⑥B和C ⑦A、B和C
50÷7=7(人)……1(人)
7+1=8(人)
答:每人有7种选择方式。这个班订相同刊物的至少有8人。
3.把若干枝花插入5个花瓶里,不管怎么放,要保证总有一个花瓶里至少插10枝花,那么花的总数至少应该有多少枝?
5×(10-1)+1=46(枝)
答:花的总数至少应该有46枝。
至少数=商+1
抽屉数
物体总数÷抽屉数=商……余数
鸽巢数
物体数
答:全班45名同学至少有12名同学的得分是相同的。
45÷4 = 11(名)……1(名)
11 + 1= 12(名)
?
想一想,3道题总得分总共有( )种情况。
做对 没做/做错 得分
3题 0题 9分
2题 1题 6分
1题 2题 3分
0题 3题 0分
4
有3道测试题,每做对一题得3分,没做或做错不得分。全班45名同学至少有几名同学的得分是相同的?
这节课有什么收获呢?
鸽巢问题的一般形式:
把m个物体放入n个抽屉里(m>n),如果m÷n=k……b,那么总有一个抽屉里至少放入(k+1)个物体。
鸽巢问题的一般形式
(kn+a)÷n=k……a
把(kn+a)(a
鸽巢问题的一般形式
第五单元 数学广角——鸽巢问题
鸽巢原理
谁能说一说上节课我们学习了什么?
(n+1) 只鸽子飞进n个鸽巢里,(n是非0自然数),总有1个鸽巢里至少飞进2只鸽子。
这种原理叫作鸽巢原理,也叫抽屉原理。
列举法
你能用哪些方法解决问题?
假设所有鸽巢都飞进一个,剩下的1个就要飞进其中的一个鸽巢。
假设法
2
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
想一想,你能怎样放呢?
如果每个抽屉最多放2本,那么3个抽屉最多放6本,可题目要求放的是7本书。所以……
我随便放放看,
一个抽屉1本,
一个抽屉2本,
一个抽屉4本。
把7本书分成3份,尽量平均分,多出的1本总要放进其中1个抽屉里。
2
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
与同伴实践操作一下验证你的想法吧!
2
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
7
7
0
0
列举法
7
6
1
0
7
5
2
0
7
5
1
1
7
4
3
0
7
4
2
1
7
3
3
1
7
3
2
2
把7分解成3个数,共有8种情况,在任何一种情况中,总有一个数不小于3。
2
把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
7÷3=2(本)……1(本)
余下的一本放在哪个抽屉都导致“总有一个抽屉至少有3本书”。
假设法
小组讨论:如果有8本书会怎样呢?
8÷3=2(本)……2(本)
余下的2本放在哪个抽屉都导致“总有一个抽屉至少有3本书”。
如果有9本书会怎样呢?
9÷3=3(本)
有10本书呢?
10÷3=3(本)……1(本)
余下的一本放在哪个抽屉都导致“总有一个抽屉至少有4本书”。
7 ÷ 3 = 2(本)…… 1(本)
8 ÷ 3 = 2 (本)…… 2(本)
10 ÷ 3 = 3 (本)…… 1(本)
总本数
抽屉数
平均每个抽屉放进的本数
剩下的本数
物体数
剩下1本,任选其中一个抽屉放进去。
剩下2本,任选其中1个或2个抽屉放进去。
整理这些算式,你发现了什么?
7÷3 = 2(本)…… 1(本)
8÷3 = 2(本)…… 2(本)
10÷3 = 3(本)…… 1(本)
3 + 1=4(本)
2 + 1=3(本)
2 + 1= 3(本)
抽屉数
物体数
商
余数
商+1
至少数
余数不论是多少,都加1。
如果物体数除以抽屉数有余数,用所得的商加1,就会发现“总有一个抽屉里至少有商加1个物体”。
至少数=商+1
整理这些算式,你发现了什么?
(kn+a)÷n=k……a
把(kn+a)(a
8÷3=2(本)…… 2(本)
10÷3=3(本)…… 1(本)
答:把8本书放进3个抽屉里,总有一个抽屉至少放进3本书。
答:把10本书放进3个抽屉里,总有一个抽屉至少放进4本书。
至少数=商+1
2+1=3(本)
3+1=4(本)
如果有8本书会怎样呢?
10本呢?
选自教材第68页做一做第1题
1
11÷4 = 2(只)……3(只)
2 + 1 = 3(只)
11只鸽子飞进了4个鸽笼,总有1个鸽笼至少飞进了3只鸽子。为什么?
余下的3只,不论怎么飞,总有
1个鸽笼里至少再飞进1只鸽子。
选自教材第68页做一做第2题
2
色一定和前8人中的2人重复。
假设前8人每2人拿的花色一样,
那么第9个人拿的牌花
所以至少有3张牌是相
小明表演扑克牌“魔术”。一副扑克牌,取出大小王,还剩52张牌,9人每人随意抽1张,至少有3张牌是相同的花色。你理解这个扑克牌“魔术”的道理吗?
52张扑克牌里只有黑桃、红桃、梅花、方片4种花色。
9÷4 = 2(张)……1(张)
同的花色。
2 + 1 = 3(张)
1.把鸽子放进对应的笼子中,完成下表:
鸽子只数 笼子的个数 结果
6 5
总有一个笼子里至少放进( )
只鸽子。
7 6
10 9
100 99
2
只要放的鸽子数比笼子的数量多1,那么总有一个笼子里至少放进2只鸽子。
2.六年级三班,有50人,每人至少订一份学习刊物,现有A、B、C三种刊物,每人有几种选择方式?这个班订相同刊物的至少有多少人?
把有几种选择方式,看作抽屉数。
①A ②B ③C ④A和B ⑤A和C ⑥B和C ⑦A、B和C
50÷7=7(人)……1(人)
7+1=8(人)
答:每人有7种选择方式。这个班订相同刊物的至少有8人。
3.把若干枝花插入5个花瓶里,不管怎么放,要保证总有一个花瓶里至少插10枝花,那么花的总数至少应该有多少枝?
5×(10-1)+1=46(枝)
答:花的总数至少应该有46枝。
至少数=商+1
抽屉数
物体总数÷抽屉数=商……余数
鸽巢数
物体数
答:全班45名同学至少有12名同学的得分是相同的。
45÷4 = 11(名)……1(名)
11 + 1= 12(名)
?
想一想,3道题总得分总共有( )种情况。
做对 没做/做错 得分
3题 0题 9分
2题 1题 6分
1题 2题 3分
0题 3题 0分
4
有3道测试题,每做对一题得3分,没做或做错不得分。全班45名同学至少有几名同学的得分是相同的?
这节课有什么收获呢?
鸽巢问题的一般形式:
把m个物体放入n个抽屉里(m>n),如果m÷n=k……b,那么总有一个抽屉里至少放入(k+1)个物体。
鸽巢问题的一般形式
(kn+a)÷n=k……a
把(kn+a)(a
