六年级下册数学人教版4.2.1 正比例课件(共27张PPT)
文档属性
| 名称 | 六年级下册数学人教版4.2.1 正比例课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 19:46:22 | ||
图片预览






文档简介
(共27张PPT)
第5课时 正比例
第四单元 比例
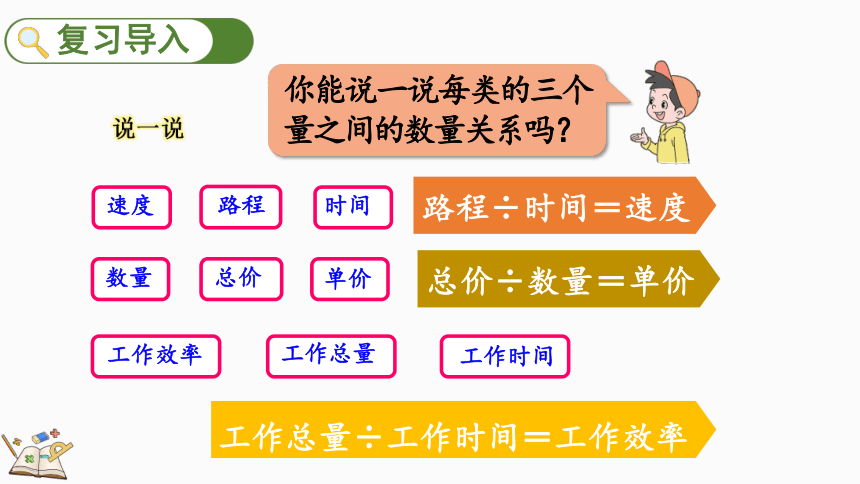
你能说一说每类的三个量之间的数量关系吗?
说一说
速度
时间
路程
路程÷时间=速度
总价
数量
单价
总价÷数量=单价
工作效率
工作总量
工作时间
工作总量÷工作时间=工作效率
文具店有一种彩带,销售的数量与总价的关系如下表。
1
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
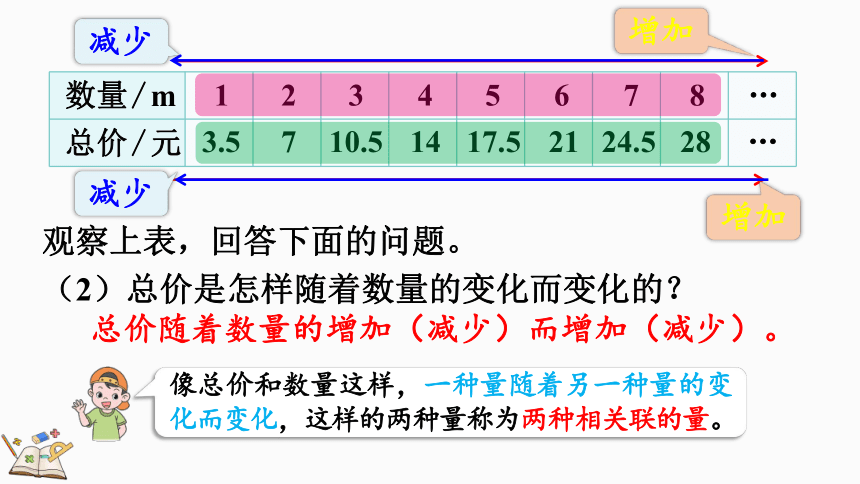
观察上表,回答下面的问题。
(1)表中有哪两种量?
通过观察上表可知表中有数量与总价这两种量。
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
观察上表,回答下面的问题。
(2)总价是怎样随着数量的变化而变化的?
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
增加
增加
减少
减少
像总价和数量这样,一种量随着另一种量的变化而变化,这样的两种量称为两种相关联的量。
总价随着数量的增加(减少)而增加(减少)。
观察上表,回答下面的问题。
(3)相应的总价与数量的比分别是多少?比值是
多少?
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
=
3.5
=
3.5
=
3.5
……
=
3.5
=
3.5
=
3.5
=
3.5
=
3.5
比值一定
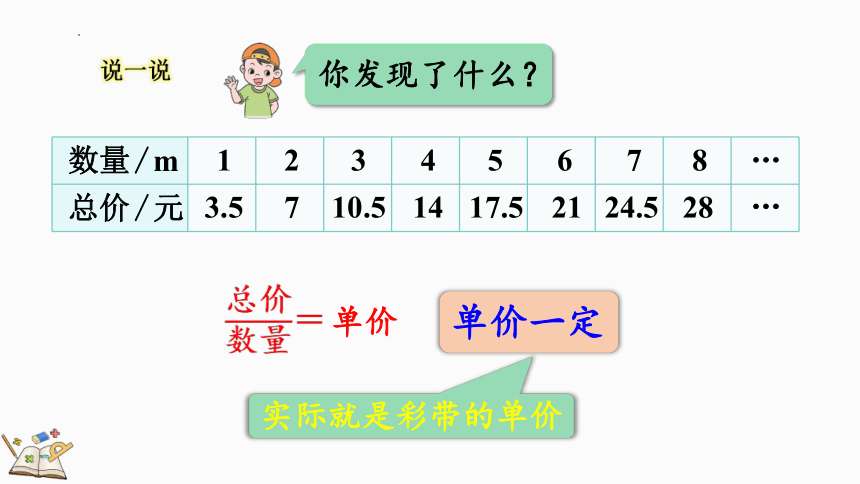
说一说
你发现了什么?
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
单价一定
=
单价
实际就是彩带的单价
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
上表中,总价和数量是成正比例的量,二者成正比例关系。
如果用字母y和x表示两种相关联的量,
用k表示它们的比值(一定)。
正比例关系可以用下面的式子表示:
= k
(一定)
想一想
两种量成正比例关系要满足什么条件?
两种量成正比例关系要满足以下三个条件:
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的比值(也
就是商)一定。
0
2
4
6
8
10
12
14
数量/m
49
42
35
28
21
14
7
总价/元
上页表中的数据还可以用图象(如下图)表示:
(1)从图象中你发现了什么?
根据图象回答下面的问题:
正比例关系图象是一条从(0,0)出发的无限延伸的射线。
彩带的数量增加,总价也增加,总价和数量是两种相关联的量。
0
2
4
6
8
10
12
14
数量/m
49
42
35
28
21
14
7
总价/元
上页表中的数据还可以用图象(如下图)表示:
(2)把数对(10,35)和
(12,42)所在的点
描出来,并和上面的
图象连起来再延长,
你还能发现什么?
根据图象回答下面的问题:
这两点也在这条射线上。
0
2
4
6
8
10
12
14
数量/m
49
42
35
28
21
14
7
总价/元
上页表中的数据还可以用图象(如下图)表示:
(3)不计算,根据图象判
断,如果买9 m彩带,
总价是多少?49元能
买多少米彩带?
根据图象回答下面的问题:
31.5元
14 m
0
2
4
6
8
10
12
14
数量/m
49
42
35
28
21
14
7
总价/元
上页表中的数据还可以用图象(如下图)表示:
(4)小明买的彩带的米数
是小丽的2倍,他花
的钱是小丽的几倍?
根据图象回答下面的问题:
答:因为彩带的数量成倍地增加,
总价也会成倍地增加,所以
他花的钱是小丽的2倍。
彩带的单价一定
42÷21=2
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
说一说
……
一辆汽车行驶的时间和路程如下表。
做一做
选自教材第44页做一做
(1)写出几组路程与相对应的时间的比,并比较比
值的大小。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
=
160
2
80
=
240
30
80
=
80
1
80
比值相等,都是80。
一辆汽车行驶的时间和路程如下表。
选自教材第44页做一做
(2)说一说这个比值表示什么。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
比值表示汽车的行驶速度。
=
路程
时间
速度
一辆汽车行驶的时间和路程如下表。
选自教材第44页做一做
(4)在图中描出表示路程和相对应时间的点,然后
把它们按顺序连起来。估计一下行驶120 km
大约要用多长时间。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
路程/km
480
400
320
240
160
80
0
1
2
3
4
5
6
时间/时
行驶120km大约要用1.5小时。
下面各题中的两种量成正比例吗 成正比例的画“√”,不成
正比例的画“ ”。
(1)每小时织布的米数一定,织布的总米数与时间。( )
√
×
√
(2)人的身高与体重。 ( )
(3)某报刊的单价一定,订阅费用与数量。 ( )
请问总价与篮球的数量是不是成正比例关系, 如果成正比例关系, 在什么情况下呢
1.现在某体育用品店声称:如果买的足球不超过100个,每个72元;如果买的篮球不少于100个,每个70元。
总价÷数量=单价,当单价一定时,总价与数量成正比例关系。
买的篮球不超过100个,单价固定为每个72元;买的篮球不少于100个,单价固定为每个70元。
成正比例关系
2.完成表格,画图判断:哪一张表格的变化情况成正比例关系?为什么?
正方形边长/cm 正方形
面积/cm2
1 1
2
3
4
正方形 边长/cm 正方形
周长/cm
1 4
2
3
4
8
12
16
4
9
16
(2)
(1)
正方形边长/cm 正方形
面积/cm2
1 1
2
3
4
4
9
16
(1)
1
2
3
4
2
6
4
10
8
12
14
16
0
面积/cm2
边长/cm
图象不是射线,不成正比例关系。
正方形 边长/cm 正方形
周长/cm
1 4
2
3
4
8
12
16
(2)
1
2
3
4
2
6
4
10
8
12
14
16
0
边长/cm
周长/cm
图象是经过(0,0)的射线,成正比例关系。
这节课有什么收获呢?
正比例
成正比例的量是两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
这节课有什么收获呢?
正比例
如果用字母y和x表示两种相关联的量,
用k表示它们的比值(一定)。
正比例关系可以用下面的式子表示:
= k
(一定)
图像:是一条从(0,0)出发的无限延伸的射线。
正比例
两种相关联的量
比值一定
= k
(一定)
正比例关系图象的特点:
是一条从(0,0)出发的无限延伸的射线
第5课时 正比例
第四单元 比例
你能说一说每类的三个量之间的数量关系吗?
说一说
速度
时间
路程
路程÷时间=速度
总价
数量
单价
总价÷数量=单价
工作效率
工作总量
工作时间
工作总量÷工作时间=工作效率
文具店有一种彩带,销售的数量与总价的关系如下表。
1
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
观察上表,回答下面的问题。
(1)表中有哪两种量?
通过观察上表可知表中有数量与总价这两种量。
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
观察上表,回答下面的问题。
(2)总价是怎样随着数量的变化而变化的?
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
增加
增加
减少
减少
像总价和数量这样,一种量随着另一种量的变化而变化,这样的两种量称为两种相关联的量。
总价随着数量的增加(减少)而增加(减少)。
观察上表,回答下面的问题。
(3)相应的总价与数量的比分别是多少?比值是
多少?
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
=
3.5
=
3.5
=
3.5
……
=
3.5
=
3.5
=
3.5
=
3.5
=
3.5
比值一定
说一说
你发现了什么?
数量/m
总价/元
1
2
3
4
5
6
7
8
3.5
7
10.5
14
17.5
21
24.5
28
…
…
单价一定
=
单价
实际就是彩带的单价
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
上表中,总价和数量是成正比例的量,二者成正比例关系。
如果用字母y和x表示两种相关联的量,
用k表示它们的比值(一定)。
正比例关系可以用下面的式子表示:
= k
(一定)
想一想
两种量成正比例关系要满足什么条件?
两种量成正比例关系要满足以下三个条件:
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的比值(也
就是商)一定。
0
2
4
6
8
10
12
14
数量/m
49
42
35
28
21
14
7
总价/元
上页表中的数据还可以用图象(如下图)表示:
(1)从图象中你发现了什么?
根据图象回答下面的问题:
正比例关系图象是一条从(0,0)出发的无限延伸的射线。
彩带的数量增加,总价也增加,总价和数量是两种相关联的量。
0
2
4
6
8
10
12
14
数量/m
49
42
35
28
21
14
7
总价/元
上页表中的数据还可以用图象(如下图)表示:
(2)把数对(10,35)和
(12,42)所在的点
描出来,并和上面的
图象连起来再延长,
你还能发现什么?
根据图象回答下面的问题:
这两点也在这条射线上。
0
2
4
6
8
10
12
14
数量/m
49
42
35
28
21
14
7
总价/元
上页表中的数据还可以用图象(如下图)表示:
(3)不计算,根据图象判
断,如果买9 m彩带,
总价是多少?49元能
买多少米彩带?
根据图象回答下面的问题:
31.5元
14 m
0
2
4
6
8
10
12
14
数量/m
49
42
35
28
21
14
7
总价/元
上页表中的数据还可以用图象(如下图)表示:
(4)小明买的彩带的米数
是小丽的2倍,他花
的钱是小丽的几倍?
根据图象回答下面的问题:
答:因为彩带的数量成倍地增加,
总价也会成倍地增加,所以
他花的钱是小丽的2倍。
彩带的单价一定
42÷21=2
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
说一说
……
一辆汽车行驶的时间和路程如下表。
做一做
选自教材第44页做一做
(1)写出几组路程与相对应的时间的比,并比较比
值的大小。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
=
160
2
80
=
240
30
80
=
80
1
80
比值相等,都是80。
一辆汽车行驶的时间和路程如下表。
选自教材第44页做一做
(2)说一说这个比值表示什么。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
比值表示汽车的行驶速度。
=
路程
时间
速度
一辆汽车行驶的时间和路程如下表。
选自教材第44页做一做
(4)在图中描出表示路程和相对应时间的点,然后
把它们按顺序连起来。估计一下行驶120 km
大约要用多长时间。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
路程/km
480
400
320
240
160
80
0
1
2
3
4
5
6
时间/时
行驶120km大约要用1.5小时。
下面各题中的两种量成正比例吗 成正比例的画“√”,不成
正比例的画“ ”。
(1)每小时织布的米数一定,织布的总米数与时间。( )
√
×
√
(2)人的身高与体重。 ( )
(3)某报刊的单价一定,订阅费用与数量。 ( )
请问总价与篮球的数量是不是成正比例关系, 如果成正比例关系, 在什么情况下呢
1.现在某体育用品店声称:如果买的足球不超过100个,每个72元;如果买的篮球不少于100个,每个70元。
总价÷数量=单价,当单价一定时,总价与数量成正比例关系。
买的篮球不超过100个,单价固定为每个72元;买的篮球不少于100个,单价固定为每个70元。
成正比例关系
2.完成表格,画图判断:哪一张表格的变化情况成正比例关系?为什么?
正方形边长/cm 正方形
面积/cm2
1 1
2
3
4
正方形 边长/cm 正方形
周长/cm
1 4
2
3
4
8
12
16
4
9
16
(2)
(1)
正方形边长/cm 正方形
面积/cm2
1 1
2
3
4
4
9
16
(1)
1
2
3
4
2
6
4
10
8
12
14
16
0
面积/cm2
边长/cm
图象不是射线,不成正比例关系。
正方形 边长/cm 正方形
周长/cm
1 4
2
3
4
8
12
16
(2)
1
2
3
4
2
6
4
10
8
12
14
16
0
边长/cm
周长/cm
图象是经过(0,0)的射线,成正比例关系。
这节课有什么收获呢?
正比例
成正比例的量是两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
这节课有什么收获呢?
正比例
如果用字母y和x表示两种相关联的量,
用k表示它们的比值(一定)。
正比例关系可以用下面的式子表示:
= k
(一定)
图像:是一条从(0,0)出发的无限延伸的射线。
正比例
两种相关联的量
比值一定
= k
(一定)
正比例关系图象的特点:
是一条从(0,0)出发的无限延伸的射线
