2024年中考数学总复习验收卷(七)(含解析)
文档属性
| 名称 | 2024年中考数学总复习验收卷(七)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 20:20:33 | ||
图片预览



文档简介
2024年中考数学总复习验收卷(七)
数学试卷
考试范围:初中;考试时间:120分钟;满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题只有一个正确答案,每小题3分,满分30分)
1.的倒数是( )
A.2023 B. C. D.
2.下列手机手势解锁图案中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.一个人做“抛硬币”游戏,抛10次,反面朝上7次,下列说法正确的是( )
A.反面朝上的频率是7 B.反面朝上的频数是0.7
C.正面朝上的频数是3 D.正面朝上的频率是3
5.已知直线,将一块含30°角的直角三角板,按如图所示方式放置,其中A、B两点分别落在直线m、n上,若,则的度数是( )
A. B. C. D.
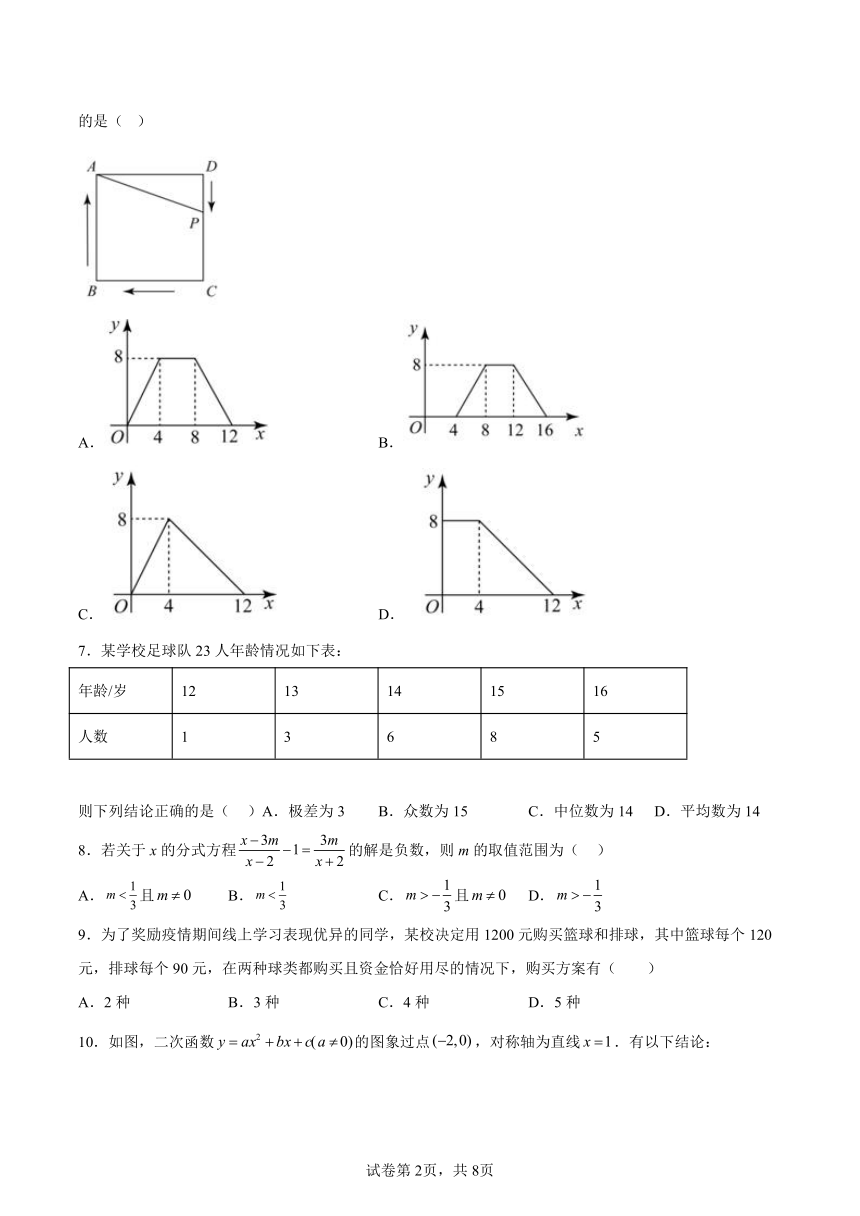
6.如图,已知正方形 的边长为 , 从顶点 出发沿正方形的边运动,路线是 ,设 点经过的路程为 , 的面积是 ,则下列图象能大致反映 与 的函数关 系的是( )
A. B.
C. D.
7.某学校足球队23人年龄情况如下表:
年龄/岁 12 13 14 15 16
人数 1 3 6 8 5
则下列结论正确的是( )A.极差为3 B.众数为15 C.中位数为14 D.平均数为14
8.若关于x的分式方程的解是负数,则m的取值范围为( )
A.且 B. C.且 D.
9.为了奖励疫情期间线上学习表现优异的同学,某校决定用1200元购买篮球和排球,其中篮球每个120元,排球每个90元,在两种球类都购买且资金恰好用尽的情况下,购买方案有( )
A.2种 B.3种 C.4种 D.5种
10.如图,二次函数的图象过点,对称轴为直线.有以下结论:
①;
②;
③若(,),(,)是抛物线上的两点,当时,;
④点,是抛物线与轴的两个交点,若在轴下方的抛物线上存在一点,使得⊥,则的取值范围为;
⑤若方程的两根为,,且<,则﹣2≤<<4.
其中正确结论的序号是( )
A.①②④ B.①③④
C.①③⑤ D.①②③⑤
二、填空题(每小题3分,满分21分)
11.韩城市为了能源结构优化、生态环境保护,以及推动绿色低碳高质量发展,计划投产大唐西庄农光互补光伏发电项目,总投资470000000元.将数据470000000用科学记数法表示为_________________.
12.函数的自变量x的取值范围是___.
13.如图,在和中,点A,,,在同一直线上,,,只添加一个条件:____________能判定.
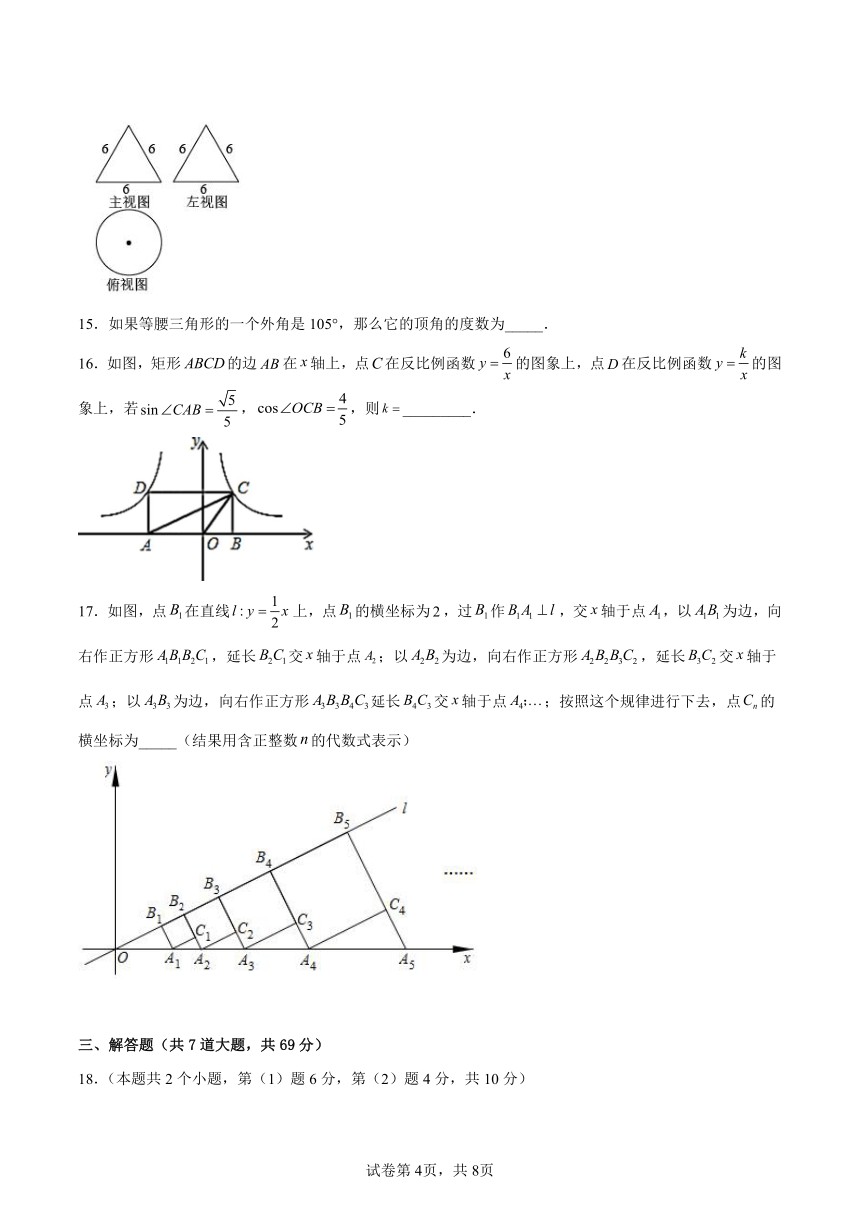
14.如图为某几何体的三视图(单位:cm),则该几何体的侧面积等于______.
15.如果等腰三角形的一个外角是105°,那么它的顶角的度数为_____.
16.如图,矩形的边在轴上,点在反比例函数的图象上,点在反比例函数的图象上,若,,则_________.
17.如图,点在直线上,点的横坐标为,过作,交轴于点,以为边,向右作正方形,延长交轴于点;以为边,向右作正方形,延长交轴于点;以为边,向右作正方形延长交轴于点;按照这个规律进行下去,点的横坐标为_____(结果用含正整数的代数式表示)
三、解答题(共7道大题,共69分)
18.(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)计算:
(2)因式分解:
19.(本题满分5分)解方程:.
20.(本题满分8分)由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习方式:网上自测,网上阅读,网上答疑,网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如下两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)本次共调查了______名学生;
(2)在扇形统计图中,的值是______,对应的扇形圆心角的度数是______;
(3)请补全条形统计图;
(4)若该校共有2000名学生,根据抽样调查的结果,请你估计该校最喜欢方式的学生人数.
21.(本题满分10分)如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若AC=10,CD=6,求DE的长.
22.(本题满分10分)小明星期天上午8:00从家出发到离家36千米的书城买书,他先从家出发骑公共自行车到公交车站,等了12分钟的车,然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变,公交车匀速行驶,小明家、公交车站、书城依次在一条笔直的公路旁).如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象,其中线段AB对应的函数表达式为y=kx+6.
(1)求小明骑公共自行车的速度;
(2)求线段CD对应的函数表达式;
(3)求出发时间x在什么范围时,小明离公交车站的路程不超过3千米?
综合与实践(本题满分12分)
如图1,在直角三角形纸片ABC中,∠BAC=90°,AB=6,AC=8.
【数学活动】
将三角形纸片ABC进行以下操作:第一步:折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE;第二步:将△ABC沿折痕DE展开,然后将△DEC绕点D逆时针方向旋转得到△DFG,点E,C的对应点分别是点F,G,直线GF与边AC交于点M(点M不与点A重合),与边AB交于点N.
(1)【数学思考】
折痕DE的长为 ;
(2)在△DEC绕点D旋转的过程中,试判断MF与ME的数量关系,并证明你的结论;
(3)【数学探究】
在△DEC绕点D旋转的过程中,探究下列问题:
①如图2,当直线GF经过点B时,AM的长为 ;
②如图3,当直线GFBC时,求AM的长;
(4)【问题延伸】
在△DEC绕点D旋转的过程中,连接AF,则AF的最小值为 .
24.综合与探究(本题满分14分)
已知:、是方程的两个实数根,且,抛物线的图像经过点、.
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与轴的另一交点为,抛物线的顶点为,试求出点、的坐标和的面积;
(3)是线段上的一点,过点作轴,与抛物线交于点,若直线把分成面积之比为的两部分,请直接写出点的坐标 ;
(4)若点在直线上,点在平面上,直线上是否存在点,使以点、点、点、点为顶点的四边形为菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数求解即可.
【详解】解:∵,
∴的倒数是.
故选C.
【点睛】本题考查了倒数的定义,熟练掌握倒数的定义是解答本题的关键.正数的倒数是正数,负数的倒数是负数,0没有倒数.
2.B
【分析】根据轴对称图形与中心对称图形的概念求解.
【详解】解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;
B、不是轴对称图形,是中心对称图形,故此选项符合题意;
C、既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
D、是轴对称图形,不是中心对称图形,故此选项不合题意.
故选:B.
【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
3.C
【分析】分别根据同底数幂的乘除法法则,合并同类项的法则,幂的乘方的运算法则,逐一判断即可.
【详解】解:A. ,故本选项错误,不符合题意;
B. ,故本选项错误,不符合题意;
C. ,故本选项正确,符合题意;
D. ,故本选项错误,不符合题意;
故选:C.
【点睛】本题考查了同底数幂的乘除法法则,合并同类项的法则,幂的乘方的运算法则,解题的关键是熟记相关法则并灵活运用.
4.C
【分析】根据频率等于频数除以数据总和进行计算,然后选择即可.
【详解】解:∵一个人做“抛硬币”游戏,抛10次,反面朝上7次,
∴反面朝上的频率是,即,反面朝上的频数是7,
正面朝上的频率是,即,正面朝上的频数是3,
故选:C.
【点睛】此题考查了频数与频率,熟练掌握频数与频率的定义是解本题的关键.
5.D
【分析】利用平行线的性质求出即可解决问题.
【详解】解:如图,
∵,
∴,
由题意知:,
∴,
∴,
故选:D.
【点睛】本题考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
6.A
【分析】当点在上运动时,随着的增大而增大,当点在上运动时,不变,据此作出选择即可.
【详解】解:当点在上运动,即时,随着的增大而增大;
当点在上运动,即时,不变;
当点在上运动,即时,随的增大而减小.
故选:A.
【点睛】本题考查了动点问题的函数图象,解决动点问题的函数图象问题关键是发现随的变化而变化的趋势.
7.B
【分析】根据众数、中位数、平均数与极差的定义逐一计算即可判断.
【详解】A、极差为16-12=4,错误;
B、这23个数据的众数为15,正确;
C、共23人,排序后第12人的岁数是中位数,中位数为15,错误;
D、平均数为=14.6,错误;
故选B.
【点睛】本题主要考查众数、极差、中位数和平均数,熟练掌握众数、极差、中位数和平均数的定义是解题的关键.
8.A
【分析】先解关于x的分式方程,然后根据分式方程的解是负数和分式成立的条件分别列关于m的一元一次不等式求解,即可得到m的范围.
【详解】解:,
去分母得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为1得:,
∵分式方程的解是负数,
∴,
∴ ,
∴,
∵且,
∴,
∵,
解得且,
∴且.
故选:A.
【点睛】本题考查解分式方程和分式方程的解,解不等式,以及分式有意义的条件,熟练掌握分式方程的解法,注意方程增根的情况是解题的关键.
9.B
【分析】设购买篮球x个,排球y个,根据“购买篮球的总钱数+购买排球的总钱数=1200”列出关于x、y的方程,由x、y均为正整数即可得.
【详解】解:设购买篮球x个,排球y个,
根据题意可得120x+90y=1200,
则y=,
∵x、y均为正整数,
∴x=1、y=12或x=4、y=8或x=7、y=4,
所以两种球类都购买且购买资金恰好用尽的情况下,购买方案有3种,
故选:B.
【点睛】本题考查二元一次方程的应用,解题的关键是理解题意,依据相等关系列出方程,注意篮球和排球个数都是正整数.
10.B
【分析】根据二次函数的图象与性质即可求出答案.
【详解】①由图象可知:a>0,c<0,
>0,
∴abc>0,故①正确;
②∵抛物线的对称轴为直线x=1,抛物线的对称轴为直线x=1,
∴ =1,
∴b=-2a,
当x=-2时,y=4a-2b+c=0,
∴4a+4a+c=0,
∴8a+c=0,故②错误;
③∵A(x1,m),B(x2,m)是抛物线上的两点,
由抛物线的对称性可知:x1+x2=1×2=2,
∴当x=2时,y=4a+2b+c=4a-4a+c=c,故③正确;
④由题意可知:M,N到对称轴的距离为3,
当抛物线的顶点到x轴的距离不小于3时,
在x轴下方的抛物线上存在点P,使得PM⊥PN,
即,
∵8a+c=0,
∴c=-8a,
∵b=-2a,
∴,
解得:a≥,故④错误;
⑤易知抛物线与x轴的另外一个交点坐标为(4,0),
∴y=ax2+bx+c=a(x+2)(x-4)
若方程a(x+2)(4-x)=-2,
即方程a(x+2)(x-4)=2的两根为x1,x2,
则x1、x2为抛物线与直线y=2的两个交点的横坐标,
∵x1<x2,
∴x1<-2<4<x2,故⑤错误;
故选:B.
【点睛】本题考查二次函数,解题的关键是熟练运用二次函数的图象与性质,本题属于基础题型.
11.
【分析】对于一个绝对值较大的数,用科学记数法写成的形式,其中,n是比原整数位数少1的数.
【详解】.
故答案为:.
【点睛】此题考查了正整数指数科学记数法,对于一个绝对值大于10的数,科学记数法的表示形式为的形式,其中,n为整数,表示时关键要正确确定a的值以及n的值.
12.x>3
【分析】根据二次根式的意义的条件,被开方数大于或等于0,分母不等于0,可以求出x的范围.
【详解】解:根据题意得:x-1≥0且x-3>0,
解得:x>3,
故答案为:x>3.
【点睛】考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
13.或或(填写一个即可)
【分析】根据全等三角形的判定定理可进行求解.
【详解】解:∵,
∴,
∵,
∴当添加时,则可根据“”判定;
当添加时,则可根据“”判定;
当添加时,则可根据“”判定;
故答案为或或(填写一个即可).
【点睛】本题主要考查全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
14.
【分析】根据三视图易得此几何体为圆锥,再根据圆锥侧面积公式(底面周长×母线长)可计算出结果.
【详解】由题意得底面直径为,母线长为,
∴几何体的侧面积为,
故答案为.
【点睛】此题主要考查了由三视图判断几何体,以及圆锥的侧面积公式的应用,关键是判断几何体的形状.
15.75°或30°.
【详解】试题解析:∵一个外角为105°,
∴三角形的一个内角为75°,
当75°为顶角时,顶角为75°,
当75°为底角时,顶角为30°,
所以等腰三角形的顶角为75°或30°.
考点:等腰三角形的性质.
16.-10
【分析】设C(x,),根据求出OB,BC,再根据求出AC,由勾股定理求出AB,从而得出AO,得到D的坐标,进而求出k的值.
【详解】解:设C(x,)(x>0),
,,
∵四边形ABCD是矩形,
,,
,
,
,即,
解得,,(舍去),
,,
,
,即,
,
,
,
,
∵D在函数的图象上,
.
故答案为:-10.
【点睛】此题是一道综合性较强的题目,将解直角三角形和用待定系数法求函数解析式结合起来,有一定难度.
17.
【分析】过点分别作轴,轴,轴,
轴,轴,……垂足分别为,根据题意求出,得到图中所有的直角三角形都相似,两条直角边的比都是可以求出点的横坐标为:,再依次求出……即可求解.
【详解】解:过点分别作轴,轴,轴,
轴,轴,……垂足分别为
点在直线上,点的横坐标为,
点的纵坐标为,
即:
图中所有的直角三角形都相似,两条直角边的比都是
点的横坐标为:,
点的横坐标为:
点C3的横坐标为:
点的横坐标为:
点的横坐标为:
故答案为
【点睛】本题考查的是规律,熟练掌握相似三角形的性质是解题的关键.
18.(1);(2)
【详解】(1)解:原式
;
(2)解:
19. ,
【分析】方程变形后,利用平方差公式分解,利用两数相乘积为,两因式中至少有一个为转化为两个一元一次方程来求解.
【详解】解:方程变形得:,
分解因式得:,
开可得:或,
解得:,.
【点睛】本题考查了解一元二次方程因式分解法,熟练掌握因式分解的方法是解本题的关键.
20.(1)50;
(2)30,72°;
(3)见解析;
(4)该校最喜欢方式A的学生约有800名.
【分析】(1)用A的人数除以A的百分比即可;
(2)用B的人数除以样本容量即可;
(3)求出B的人数补全统计图即可;
(4)用2000乘以A的百分比即可.
(1)
20÷40%=50(名);
故答案为:50;
(2)
15÷50×100%=30%,即m=30;
×360°=72°;
故答案为:30,72°;
(3)
50-20-15-10=5(名);补全图形如下:
(4)
2000×40%=800(名).
答:该校最喜欢方式A的学生约有800名.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.也考查了用样本估计总体.
21.(1)见解析;(2)
【分析】(1)连接AD、OD,由圆周角的性质定理和等腰三角形的三线合一定理,即可得到答案;
(2)先求出AD的长度,然后由三角形的面积公式,即可求出答案.
【详解】解:(1)连接AD、OD, 如图:
∵ AC为⊙O的直径,
∴ ∠ADC=90°.
∵ AB=AC,
∴ 点D是BC的中点.
∵ O是AC中点,
∴ OD是△ABC的中位线.
∴ OD∥AB.
∵ DE⊥AB,
∴ OD⊥EF.
∴ DE是⊙O的切线.
(2)连接OD、AD,
∵ AB=AC,且∠ADC=90°,
在Rt△ACD中,AC=AB=10,CD=6,
∴ AD=,
又S△ACD=AB·DE =AD·BD,
即 ×10×DE=×8×6,
∴ DE=.
【点睛】本题考查了切线的判定定理,圆周角定理,等腰三角形的性质,勾股定理,解题的关键是熟练掌握所学的知识,正确的进行解题.
22.(1)10千米/小时;(2)y=30x﹣24;(3)0.3≤x≤0.9
【分析】(1)根据线段AB对应的函教表达式为y=kx+6和函数图象中的数据,可以求得k的值,然后即可得到点A的坐标,从而可以求得小明骑公共自行车的速度;
(2)根据题意,可以得到点C和点D的坐标,然后即可求得线段CD对应的函数表达式;
(3)根据前面求出的函数解析式,可以得到出发时间x在什么范围时,小明离公交车站的路程不超过3千米.
【详解】解:(1)∵线段AB对应的函教表达式为y=kx+6,点(0.6,0)在y=kx+6上,
∴0=0.6k+6,得k=﹣10,
∴y=﹣10x+6,
当x=0时,y=6,
∴小明骑公共自行车的速度为6÷0.6=10(千米/小时),
答:小明骑公共自行车的速度是10千米/小时;
(2)∵点C的横坐标为:0.6+=0.8,
∴点C的坐标为(0.8,0),
∵从8:00到9:48分是1.8小时,点D的纵坐标是36﹣6=30,
∴点D的坐标为(1.8,30),
设线段CD对应的函数表达式是y=mx+n,
,得,
即线段CD对应的函数表达式是y=30x﹣24;
(3)令﹣10x+6≤3,得x≥0.3,
令30x﹣24≤3,得x≤0.9,
即出发时间x在0.3≤x≤0.9范围时,小明离公交车站的路程不超过3千米.
【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数关系式,利用一次函数的性质和数形结合的思想解答.
23.(1)3
(2)MF=ME,证明见解析
(3)①;②3
(4)2
【分析】(1)通过证明DE是中位线,可得DE=3;
(2)连接DM,根据HL证Rt△DMF≌Rt△DME,即可得出结论;
(3)①根据角相等得出BM=MC,设MC=BM=x,根据勾股定理求出x的值,根据AM=AC-CM求出AM的值即可;②当直线GFBC时,根据相似三角形的性质求解即可;
(4)根据直角三角形斜边上的中线等于斜边的一半,求得,当三点共线时,最小,最小值等于,即可求解.
(1)
由折叠可知:AE=EC,DE⊥AC,
∴DE∥AB,
∴,
∴DC=BD,
∴DE是△ABC的中位线,
∴DE=AB=3,
故答案为:3;
(2)
MF=ME,证明如下:
连接DM,
由旋转知,DE=DF,∠DFM=∠DEM=90°,
在Rt△DMF和Rt△DME中,
,
∴Rt△DMF≌Rt△DME(),
∴MF=ME;
(3)
①∵DG=DB=DC,
∴∠G=∠DBG,
∴∠G=∠C,
∴∠MBC=∠C,
∴BM=MC,
设BM=MC=x,
在Rt△ABM中,BM2=AB2+AM2,
即62+(8-x)2=x2,
解得x=,
∴AM=AC-CM=8-;
②如图, 连接DM,当直线GFBC时,
∠BAC=90°,AB=6,AC=8,
,
设到的距离为,则,
则到的距离为,
,
,
,
,
,
(4)
如下图所示:
是直角三角形,为斜边上的中线,则
当A、D、F三点共线时,最小,最小值等于.
故答案为:2.
【点睛】本题考查了旋转的性质,全等三角形的判定和性质,勾股定理、等腰直角三角形的性质等知识,三角形中位线的性质,相似三角形的性质与判定,综合运用以上知识是解题的关键.
24.(1)y= x2 4x+5;(2)15;(3)( ,0)或( ,0);(4)存在M点,M点坐标为(7,12)或
【分析】(1)通过解方程即可求出p、q的值,那么A、B两点的坐标就可求出.然后根据A、B两点的坐标即可求出抛物线的解析式.
(2)根据(1)得出的抛物线的解析式即可求出C、D两点的坐标.由于△BCD的面积无法直接求出,可用其他图形的面积的“和,差关系”来求出.过D作DM⊥x轴于M,那么△BCD的面积=梯形DMOB的面积+△DCM的面积-△BOC的面积.由此可求出△BCD的面积.
(3)由于△PCH被直线BC分成的两个小三角形等高,因此面积比就等于底边的比.如果设PH与BC的交点为E,那么EH就是抛物线与直线BC的函数值的差,而EP就是E点的纵坐标.然后可根据直线BC的解析式设出E点的坐标,然后表示出EH,EP的长.进而可分两种情况进行讨论:①当EH=EP时;②当EH=EP时.由此可得出两个不同的关于E点横坐标的方程即可求出E点的坐标.也就求出了P点的坐标.
(4)分两种情况讨论,当CD=DM和当时,根据M点在直线BC上设出M点坐标,根据两点间距离公式列出方程即可求解出M点坐标.
【详解】解方程x2 6x+5=0,
(x 1)(x 5)=0,
得x1=5,x2=1
∵,
∴p=1,q=5
∴点A、B的坐标分别为A(1,0),B(0,5).
将A(1,0),B(0,5)的坐标分别代入y= x2+bx+c.
得
得:
∴抛物线的解析式为y= x2 4x+5
故答案为:y= x2 4x+5
(2)∵y= x2 4x+5,
令y=0,得 x2 4x+5=0,
得x1= 5,x2=1,
∴C点的坐标为( 5,0)
∵,
∴点D( 2,9)
过D作x轴的垂线交x轴于M
∴S△DMC=×9×(5 2)=
S梯形MDBO=×2×(9+5)=14,
S△BOC=×5×5=
∴S△BCD=S梯形MDBO+S△DMC S△BOC=14+ =15
故答案为:15
(3)设P点的坐标为(a,0)
∵B(0,5),C ( 5,0)
设BC直线的解析式为y=kx+b
∴
∴
∴BC所在的直线解析式为y=x+5
设PH与直线BC的交点坐标为E(a,a+5),
PH与抛物线y= x2 4x+5的交点坐标为H(a, a2 4a+5)
∵①EH=EP,
即( a2 4a+5) (a+5)=(a+5)
∴a= 或a= 5(舍去)
②EH=EP,
即( a2 4a+5) (a+5)=(a+5)
∴a= 或a= 5(舍去),
P点的坐标为( ,0)或( ,0)
故答案为:( ,0)或( ,0)
(4)①∵M在直线BC上,设M(m,m+5)
若使四边形CDMN为菱形,则CD=DM
∵C(-5,0),D(-2,9)
∴
解得m=-5或m=7
m=-5时,恰好为C点,不符合题意舍去
∴m=7
∴M(7,12)
②∵直线BC上存在一点,设
若使四边形是菱形,则
∵C(-5,0),D(-2,9)
∴
解得
∴
综上所述在直线BC上存在一点M,且以点、点、点、点为顶点的四边形为菱形,此时M点坐标为(7,12)或
故答案为:存在M点,M点坐标为(7,12)或
【点睛】本题是二次函数的综合题目,涉及了待定系数法求抛物线方程,利用面积差求图形面积,两点间距离公式求线段长,菱形的判定和性质等知识点.
答案第1页,共2页
答案第1页,共2页
数学试卷
考试范围:初中;考试时间:120分钟;满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(每小题只有一个正确答案,每小题3分,满分30分)
1.的倒数是( )
A.2023 B. C. D.
2.下列手机手势解锁图案中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.一个人做“抛硬币”游戏,抛10次,反面朝上7次,下列说法正确的是( )
A.反面朝上的频率是7 B.反面朝上的频数是0.7
C.正面朝上的频数是3 D.正面朝上的频率是3
5.已知直线,将一块含30°角的直角三角板,按如图所示方式放置,其中A、B两点分别落在直线m、n上,若,则的度数是( )
A. B. C. D.
6.如图,已知正方形 的边长为 , 从顶点 出发沿正方形的边运动,路线是 ,设 点经过的路程为 , 的面积是 ,则下列图象能大致反映 与 的函数关 系的是( )
A. B.
C. D.
7.某学校足球队23人年龄情况如下表:
年龄/岁 12 13 14 15 16
人数 1 3 6 8 5
则下列结论正确的是( )A.极差为3 B.众数为15 C.中位数为14 D.平均数为14
8.若关于x的分式方程的解是负数,则m的取值范围为( )
A.且 B. C.且 D.
9.为了奖励疫情期间线上学习表现优异的同学,某校决定用1200元购买篮球和排球,其中篮球每个120元,排球每个90元,在两种球类都购买且资金恰好用尽的情况下,购买方案有( )
A.2种 B.3种 C.4种 D.5种
10.如图,二次函数的图象过点,对称轴为直线.有以下结论:
①;
②;
③若(,),(,)是抛物线上的两点,当时,;
④点,是抛物线与轴的两个交点,若在轴下方的抛物线上存在一点,使得⊥,则的取值范围为;
⑤若方程的两根为,,且<,则﹣2≤<<4.
其中正确结论的序号是( )
A.①②④ B.①③④
C.①③⑤ D.①②③⑤
二、填空题(每小题3分,满分21分)
11.韩城市为了能源结构优化、生态环境保护,以及推动绿色低碳高质量发展,计划投产大唐西庄农光互补光伏发电项目,总投资470000000元.将数据470000000用科学记数法表示为_________________.
12.函数的自变量x的取值范围是___.
13.如图,在和中,点A,,,在同一直线上,,,只添加一个条件:____________能判定.
14.如图为某几何体的三视图(单位:cm),则该几何体的侧面积等于______.
15.如果等腰三角形的一个外角是105°,那么它的顶角的度数为_____.
16.如图,矩形的边在轴上,点在反比例函数的图象上,点在反比例函数的图象上,若,,则_________.
17.如图,点在直线上,点的横坐标为,过作,交轴于点,以为边,向右作正方形,延长交轴于点;以为边,向右作正方形,延长交轴于点;以为边,向右作正方形延长交轴于点;按照这个规律进行下去,点的横坐标为_____(结果用含正整数的代数式表示)
三、解答题(共7道大题,共69分)
18.(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)计算:
(2)因式分解:
19.(本题满分5分)解方程:.
20.(本题满分8分)由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习方式:网上自测,网上阅读,网上答疑,网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如下两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)本次共调查了______名学生;
(2)在扇形统计图中,的值是______,对应的扇形圆心角的度数是______;
(3)请补全条形统计图;
(4)若该校共有2000名学生,根据抽样调查的结果,请你估计该校最喜欢方式的学生人数.
21.(本题满分10分)如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)求证:EF是⊙O的切线;
(2)若AC=10,CD=6,求DE的长.
22.(本题满分10分)小明星期天上午8:00从家出发到离家36千米的书城买书,他先从家出发骑公共自行车到公交车站,等了12分钟的车,然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变,公交车匀速行驶,小明家、公交车站、书城依次在一条笔直的公路旁).如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象,其中线段AB对应的函数表达式为y=kx+6.
(1)求小明骑公共自行车的速度;
(2)求线段CD对应的函数表达式;
(3)求出发时间x在什么范围时,小明离公交车站的路程不超过3千米?
综合与实践(本题满分12分)
如图1,在直角三角形纸片ABC中,∠BAC=90°,AB=6,AC=8.
【数学活动】
将三角形纸片ABC进行以下操作:第一步:折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE;第二步:将△ABC沿折痕DE展开,然后将△DEC绕点D逆时针方向旋转得到△DFG,点E,C的对应点分别是点F,G,直线GF与边AC交于点M(点M不与点A重合),与边AB交于点N.
(1)【数学思考】
折痕DE的长为 ;
(2)在△DEC绕点D旋转的过程中,试判断MF与ME的数量关系,并证明你的结论;
(3)【数学探究】
在△DEC绕点D旋转的过程中,探究下列问题:
①如图2,当直线GF经过点B时,AM的长为 ;
②如图3,当直线GFBC时,求AM的长;
(4)【问题延伸】
在△DEC绕点D旋转的过程中,连接AF,则AF的最小值为 .
24.综合与探究(本题满分14分)
已知:、是方程的两个实数根,且,抛物线的图像经过点、.
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与轴的另一交点为,抛物线的顶点为,试求出点、的坐标和的面积;
(3)是线段上的一点,过点作轴,与抛物线交于点,若直线把分成面积之比为的两部分,请直接写出点的坐标 ;
(4)若点在直线上,点在平面上,直线上是否存在点,使以点、点、点、点为顶点的四边形为菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数求解即可.
【详解】解:∵,
∴的倒数是.
故选C.
【点睛】本题考查了倒数的定义,熟练掌握倒数的定义是解答本题的关键.正数的倒数是正数,负数的倒数是负数,0没有倒数.
2.B
【分析】根据轴对称图形与中心对称图形的概念求解.
【详解】解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;
B、不是轴对称图形,是中心对称图形,故此选项符合题意;
C、既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
D、是轴对称图形,不是中心对称图形,故此选项不合题意.
故选:B.
【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
3.C
【分析】分别根据同底数幂的乘除法法则,合并同类项的法则,幂的乘方的运算法则,逐一判断即可.
【详解】解:A. ,故本选项错误,不符合题意;
B. ,故本选项错误,不符合题意;
C. ,故本选项正确,符合题意;
D. ,故本选项错误,不符合题意;
故选:C.
【点睛】本题考查了同底数幂的乘除法法则,合并同类项的法则,幂的乘方的运算法则,解题的关键是熟记相关法则并灵活运用.
4.C
【分析】根据频率等于频数除以数据总和进行计算,然后选择即可.
【详解】解:∵一个人做“抛硬币”游戏,抛10次,反面朝上7次,
∴反面朝上的频率是,即,反面朝上的频数是7,
正面朝上的频率是,即,正面朝上的频数是3,
故选:C.
【点睛】此题考查了频数与频率,熟练掌握频数与频率的定义是解本题的关键.
5.D
【分析】利用平行线的性质求出即可解决问题.
【详解】解:如图,
∵,
∴,
由题意知:,
∴,
∴,
故选:D.
【点睛】本题考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
6.A
【分析】当点在上运动时,随着的增大而增大,当点在上运动时,不变,据此作出选择即可.
【详解】解:当点在上运动,即时,随着的增大而增大;
当点在上运动,即时,不变;
当点在上运动,即时,随的增大而减小.
故选:A.
【点睛】本题考查了动点问题的函数图象,解决动点问题的函数图象问题关键是发现随的变化而变化的趋势.
7.B
【分析】根据众数、中位数、平均数与极差的定义逐一计算即可判断.
【详解】A、极差为16-12=4,错误;
B、这23个数据的众数为15,正确;
C、共23人,排序后第12人的岁数是中位数,中位数为15,错误;
D、平均数为=14.6,错误;
故选B.
【点睛】本题主要考查众数、极差、中位数和平均数,熟练掌握众数、极差、中位数和平均数的定义是解题的关键.
8.A
【分析】先解关于x的分式方程,然后根据分式方程的解是负数和分式成立的条件分别列关于m的一元一次不等式求解,即可得到m的范围.
【详解】解:,
去分母得:,
去括号得:,
移项得:,
合并同类项得:,
系数化为1得:,
∵分式方程的解是负数,
∴,
∴ ,
∴,
∵且,
∴,
∵,
解得且,
∴且.
故选:A.
【点睛】本题考查解分式方程和分式方程的解,解不等式,以及分式有意义的条件,熟练掌握分式方程的解法,注意方程增根的情况是解题的关键.
9.B
【分析】设购买篮球x个,排球y个,根据“购买篮球的总钱数+购买排球的总钱数=1200”列出关于x、y的方程,由x、y均为正整数即可得.
【详解】解:设购买篮球x个,排球y个,
根据题意可得120x+90y=1200,
则y=,
∵x、y均为正整数,
∴x=1、y=12或x=4、y=8或x=7、y=4,
所以两种球类都购买且购买资金恰好用尽的情况下,购买方案有3种,
故选:B.
【点睛】本题考查二元一次方程的应用,解题的关键是理解题意,依据相等关系列出方程,注意篮球和排球个数都是正整数.
10.B
【分析】根据二次函数的图象与性质即可求出答案.
【详解】①由图象可知:a>0,c<0,
>0,
∴abc>0,故①正确;
②∵抛物线的对称轴为直线x=1,抛物线的对称轴为直线x=1,
∴ =1,
∴b=-2a,
当x=-2时,y=4a-2b+c=0,
∴4a+4a+c=0,
∴8a+c=0,故②错误;
③∵A(x1,m),B(x2,m)是抛物线上的两点,
由抛物线的对称性可知:x1+x2=1×2=2,
∴当x=2时,y=4a+2b+c=4a-4a+c=c,故③正确;
④由题意可知:M,N到对称轴的距离为3,
当抛物线的顶点到x轴的距离不小于3时,
在x轴下方的抛物线上存在点P,使得PM⊥PN,
即,
∵8a+c=0,
∴c=-8a,
∵b=-2a,
∴,
解得:a≥,故④错误;
⑤易知抛物线与x轴的另外一个交点坐标为(4,0),
∴y=ax2+bx+c=a(x+2)(x-4)
若方程a(x+2)(4-x)=-2,
即方程a(x+2)(x-4)=2的两根为x1,x2,
则x1、x2为抛物线与直线y=2的两个交点的横坐标,
∵x1<x2,
∴x1<-2<4<x2,故⑤错误;
故选:B.
【点睛】本题考查二次函数,解题的关键是熟练运用二次函数的图象与性质,本题属于基础题型.
11.
【分析】对于一个绝对值较大的数,用科学记数法写成的形式,其中,n是比原整数位数少1的数.
【详解】.
故答案为:.
【点睛】此题考查了正整数指数科学记数法,对于一个绝对值大于10的数,科学记数法的表示形式为的形式,其中,n为整数,表示时关键要正确确定a的值以及n的值.
12.x>3
【分析】根据二次根式的意义的条件,被开方数大于或等于0,分母不等于0,可以求出x的范围.
【详解】解:根据题意得:x-1≥0且x-3>0,
解得:x>3,
故答案为:x>3.
【点睛】考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
13.或或(填写一个即可)
【分析】根据全等三角形的判定定理可进行求解.
【详解】解:∵,
∴,
∵,
∴当添加时,则可根据“”判定;
当添加时,则可根据“”判定;
当添加时,则可根据“”判定;
故答案为或或(填写一个即可).
【点睛】本题主要考查全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
14.
【分析】根据三视图易得此几何体为圆锥,再根据圆锥侧面积公式(底面周长×母线长)可计算出结果.
【详解】由题意得底面直径为,母线长为,
∴几何体的侧面积为,
故答案为.
【点睛】此题主要考查了由三视图判断几何体,以及圆锥的侧面积公式的应用,关键是判断几何体的形状.
15.75°或30°.
【详解】试题解析:∵一个外角为105°,
∴三角形的一个内角为75°,
当75°为顶角时,顶角为75°,
当75°为底角时,顶角为30°,
所以等腰三角形的顶角为75°或30°.
考点:等腰三角形的性质.
16.-10
【分析】设C(x,),根据求出OB,BC,再根据求出AC,由勾股定理求出AB,从而得出AO,得到D的坐标,进而求出k的值.
【详解】解:设C(x,)(x>0),
,,
∵四边形ABCD是矩形,
,,
,
,
,即,
解得,,(舍去),
,,
,
,即,
,
,
,
,
∵D在函数的图象上,
.
故答案为:-10.
【点睛】此题是一道综合性较强的题目,将解直角三角形和用待定系数法求函数解析式结合起来,有一定难度.
17.
【分析】过点分别作轴,轴,轴,
轴,轴,……垂足分别为,根据题意求出,得到图中所有的直角三角形都相似,两条直角边的比都是可以求出点的横坐标为:,再依次求出……即可求解.
【详解】解:过点分别作轴,轴,轴,
轴,轴,……垂足分别为
点在直线上,点的横坐标为,
点的纵坐标为,
即:
图中所有的直角三角形都相似,两条直角边的比都是
点的横坐标为:,
点的横坐标为:
点C3的横坐标为:
点的横坐标为:
点的横坐标为:
故答案为
【点睛】本题考查的是规律,熟练掌握相似三角形的性质是解题的关键.
18.(1);(2)
【详解】(1)解:原式
;
(2)解:
19. ,
【分析】方程变形后,利用平方差公式分解,利用两数相乘积为,两因式中至少有一个为转化为两个一元一次方程来求解.
【详解】解:方程变形得:,
分解因式得:,
开可得:或,
解得:,.
【点睛】本题考查了解一元二次方程因式分解法,熟练掌握因式分解的方法是解本题的关键.
20.(1)50;
(2)30,72°;
(3)见解析;
(4)该校最喜欢方式A的学生约有800名.
【分析】(1)用A的人数除以A的百分比即可;
(2)用B的人数除以样本容量即可;
(3)求出B的人数补全统计图即可;
(4)用2000乘以A的百分比即可.
(1)
20÷40%=50(名);
故答案为:50;
(2)
15÷50×100%=30%,即m=30;
×360°=72°;
故答案为:30,72°;
(3)
50-20-15-10=5(名);补全图形如下:
(4)
2000×40%=800(名).
答:该校最喜欢方式A的学生约有800名.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.也考查了用样本估计总体.
21.(1)见解析;(2)
【分析】(1)连接AD、OD,由圆周角的性质定理和等腰三角形的三线合一定理,即可得到答案;
(2)先求出AD的长度,然后由三角形的面积公式,即可求出答案.
【详解】解:(1)连接AD、OD, 如图:
∵ AC为⊙O的直径,
∴ ∠ADC=90°.
∵ AB=AC,
∴ 点D是BC的中点.
∵ O是AC中点,
∴ OD是△ABC的中位线.
∴ OD∥AB.
∵ DE⊥AB,
∴ OD⊥EF.
∴ DE是⊙O的切线.
(2)连接OD、AD,
∵ AB=AC,且∠ADC=90°,
在Rt△ACD中,AC=AB=10,CD=6,
∴ AD=,
又S△ACD=AB·DE =AD·BD,
即 ×10×DE=×8×6,
∴ DE=.
【点睛】本题考查了切线的判定定理,圆周角定理,等腰三角形的性质,勾股定理,解题的关键是熟练掌握所学的知识,正确的进行解题.
22.(1)10千米/小时;(2)y=30x﹣24;(3)0.3≤x≤0.9
【分析】(1)根据线段AB对应的函教表达式为y=kx+6和函数图象中的数据,可以求得k的值,然后即可得到点A的坐标,从而可以求得小明骑公共自行车的速度;
(2)根据题意,可以得到点C和点D的坐标,然后即可求得线段CD对应的函数表达式;
(3)根据前面求出的函数解析式,可以得到出发时间x在什么范围时,小明离公交车站的路程不超过3千米.
【详解】解:(1)∵线段AB对应的函教表达式为y=kx+6,点(0.6,0)在y=kx+6上,
∴0=0.6k+6,得k=﹣10,
∴y=﹣10x+6,
当x=0时,y=6,
∴小明骑公共自行车的速度为6÷0.6=10(千米/小时),
答:小明骑公共自行车的速度是10千米/小时;
(2)∵点C的横坐标为:0.6+=0.8,
∴点C的坐标为(0.8,0),
∵从8:00到9:48分是1.8小时,点D的纵坐标是36﹣6=30,
∴点D的坐标为(1.8,30),
设线段CD对应的函数表达式是y=mx+n,
,得,
即线段CD对应的函数表达式是y=30x﹣24;
(3)令﹣10x+6≤3,得x≥0.3,
令30x﹣24≤3,得x≤0.9,
即出发时间x在0.3≤x≤0.9范围时,小明离公交车站的路程不超过3千米.
【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数关系式,利用一次函数的性质和数形结合的思想解答.
23.(1)3
(2)MF=ME,证明见解析
(3)①;②3
(4)2
【分析】(1)通过证明DE是中位线,可得DE=3;
(2)连接DM,根据HL证Rt△DMF≌Rt△DME,即可得出结论;
(3)①根据角相等得出BM=MC,设MC=BM=x,根据勾股定理求出x的值,根据AM=AC-CM求出AM的值即可;②当直线GFBC时,根据相似三角形的性质求解即可;
(4)根据直角三角形斜边上的中线等于斜边的一半,求得,当三点共线时,最小,最小值等于,即可求解.
(1)
由折叠可知:AE=EC,DE⊥AC,
∴DE∥AB,
∴,
∴DC=BD,
∴DE是△ABC的中位线,
∴DE=AB=3,
故答案为:3;
(2)
MF=ME,证明如下:
连接DM,
由旋转知,DE=DF,∠DFM=∠DEM=90°,
在Rt△DMF和Rt△DME中,
,
∴Rt△DMF≌Rt△DME(),
∴MF=ME;
(3)
①∵DG=DB=DC,
∴∠G=∠DBG,
∴∠G=∠C,
∴∠MBC=∠C,
∴BM=MC,
设BM=MC=x,
在Rt△ABM中,BM2=AB2+AM2,
即62+(8-x)2=x2,
解得x=,
∴AM=AC-CM=8-;
②如图, 连接DM,当直线GFBC时,
∠BAC=90°,AB=6,AC=8,
,
设到的距离为,则,
则到的距离为,
,
,
,
,
,
(4)
如下图所示:
是直角三角形,为斜边上的中线,则
当A、D、F三点共线时,最小,最小值等于.
故答案为:2.
【点睛】本题考查了旋转的性质,全等三角形的判定和性质,勾股定理、等腰直角三角形的性质等知识,三角形中位线的性质,相似三角形的性质与判定,综合运用以上知识是解题的关键.
24.(1)y= x2 4x+5;(2)15;(3)( ,0)或( ,0);(4)存在M点,M点坐标为(7,12)或
【分析】(1)通过解方程即可求出p、q的值,那么A、B两点的坐标就可求出.然后根据A、B两点的坐标即可求出抛物线的解析式.
(2)根据(1)得出的抛物线的解析式即可求出C、D两点的坐标.由于△BCD的面积无法直接求出,可用其他图形的面积的“和,差关系”来求出.过D作DM⊥x轴于M,那么△BCD的面积=梯形DMOB的面积+△DCM的面积-△BOC的面积.由此可求出△BCD的面积.
(3)由于△PCH被直线BC分成的两个小三角形等高,因此面积比就等于底边的比.如果设PH与BC的交点为E,那么EH就是抛物线与直线BC的函数值的差,而EP就是E点的纵坐标.然后可根据直线BC的解析式设出E点的坐标,然后表示出EH,EP的长.进而可分两种情况进行讨论:①当EH=EP时;②当EH=EP时.由此可得出两个不同的关于E点横坐标的方程即可求出E点的坐标.也就求出了P点的坐标.
(4)分两种情况讨论,当CD=DM和当时,根据M点在直线BC上设出M点坐标,根据两点间距离公式列出方程即可求解出M点坐标.
【详解】解方程x2 6x+5=0,
(x 1)(x 5)=0,
得x1=5,x2=1
∵,
∴p=1,q=5
∴点A、B的坐标分别为A(1,0),B(0,5).
将A(1,0),B(0,5)的坐标分别代入y= x2+bx+c.
得
得:
∴抛物线的解析式为y= x2 4x+5
故答案为:y= x2 4x+5
(2)∵y= x2 4x+5,
令y=0,得 x2 4x+5=0,
得x1= 5,x2=1,
∴C点的坐标为( 5,0)
∵,
∴点D( 2,9)
过D作x轴的垂线交x轴于M
∴S△DMC=×9×(5 2)=
S梯形MDBO=×2×(9+5)=14,
S△BOC=×5×5=
∴S△BCD=S梯形MDBO+S△DMC S△BOC=14+ =15
故答案为:15
(3)设P点的坐标为(a,0)
∵B(0,5),C ( 5,0)
设BC直线的解析式为y=kx+b
∴
∴
∴BC所在的直线解析式为y=x+5
设PH与直线BC的交点坐标为E(a,a+5),
PH与抛物线y= x2 4x+5的交点坐标为H(a, a2 4a+5)
∵①EH=EP,
即( a2 4a+5) (a+5)=(a+5)
∴a= 或a= 5(舍去)
②EH=EP,
即( a2 4a+5) (a+5)=(a+5)
∴a= 或a= 5(舍去),
P点的坐标为( ,0)或( ,0)
故答案为:( ,0)或( ,0)
(4)①∵M在直线BC上,设M(m,m+5)
若使四边形CDMN为菱形,则CD=DM
∵C(-5,0),D(-2,9)
∴
解得m=-5或m=7
m=-5时,恰好为C点,不符合题意舍去
∴m=7
∴M(7,12)
②∵直线BC上存在一点,设
若使四边形是菱形,则
∵C(-5,0),D(-2,9)
∴
解得
∴
综上所述在直线BC上存在一点M,且以点、点、点、点为顶点的四边形为菱形,此时M点坐标为(7,12)或
故答案为:存在M点,M点坐标为(7,12)或
【点睛】本题是二次函数的综合题目,涉及了待定系数法求抛物线方程,利用面积差求图形面积,两点间距离公式求线段长,菱形的判定和性质等知识点.
答案第1页,共2页
答案第1页,共2页
同课章节目录
