五年级下册数学人教版长方体和正方体的体积课件(共30张PPT)
文档属性
| 名称 | 五年级下册数学人教版长方体和正方体的体积课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
长方体和正方体的体积
一 情境导入,探索新知
1.什么叫体积?
3.你能比画出1cm3、1dm3、1m3的大小吗?
2.常用的体积单位有哪些?
妈妈要过生日了,淘淘想买一个蛋糕送给妈妈。你知道买哪个蛋糕比较划算吗?
怎样计算两个蛋糕的体积呢?
草莓布朗尼蛋糕
218元
芒果冰激凌慕斯蛋糕
218元
同样的价格,买到的蛋糕越多,也就是蛋糕的体积越大,就越划算!
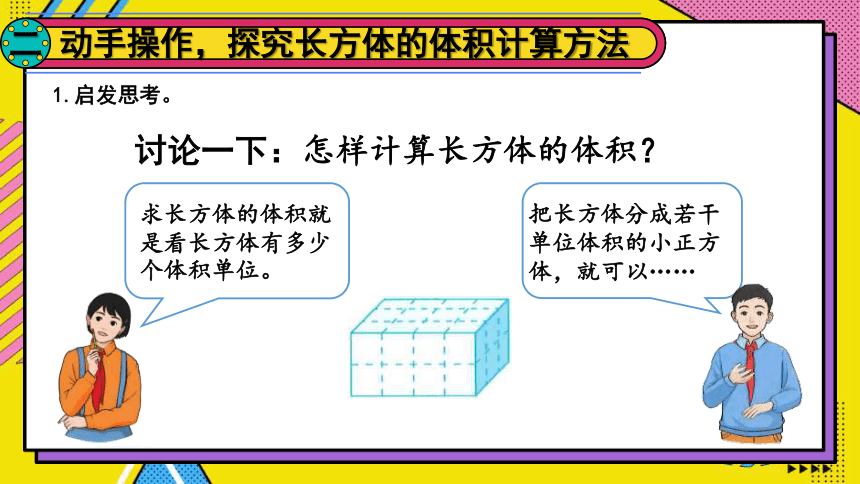
讨论一下:怎样计算长方体的体积?
求长方体的体积就是看长方体有多少个体积单位。
把长方体分成若干单位体积的小正方体,就可以……
二 动手操作,探究长方体的体积计算方法
1.启发思考。
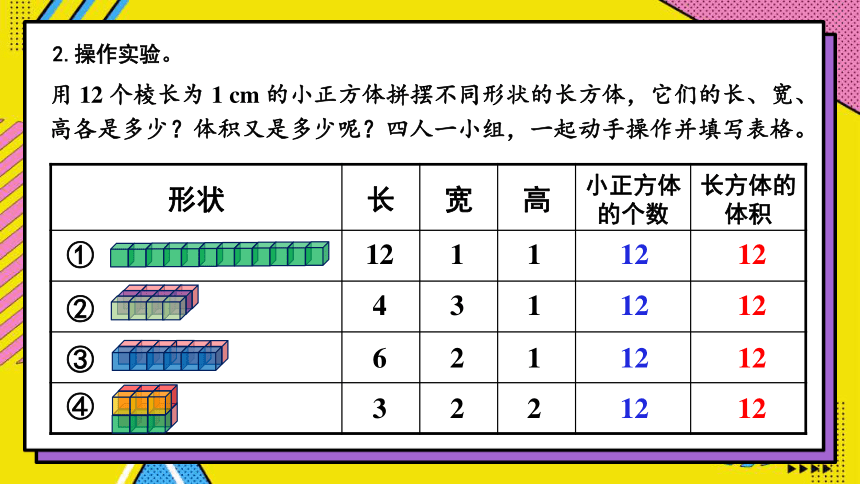
用 12 个棱长为 1 cm 的小正方体拼摆不同形状的长方体,它们的长、宽、高各是多少?体积又是多少呢?四人一小组,一起动手操作并填写表格。
2.操作实验。
形状 长 宽 高 小正方体的个数 长方体的体积
12
1
1
12
12
4
3
1
12
12
6
2
1
12
12
3
2
2
12
12
①
②
③
④
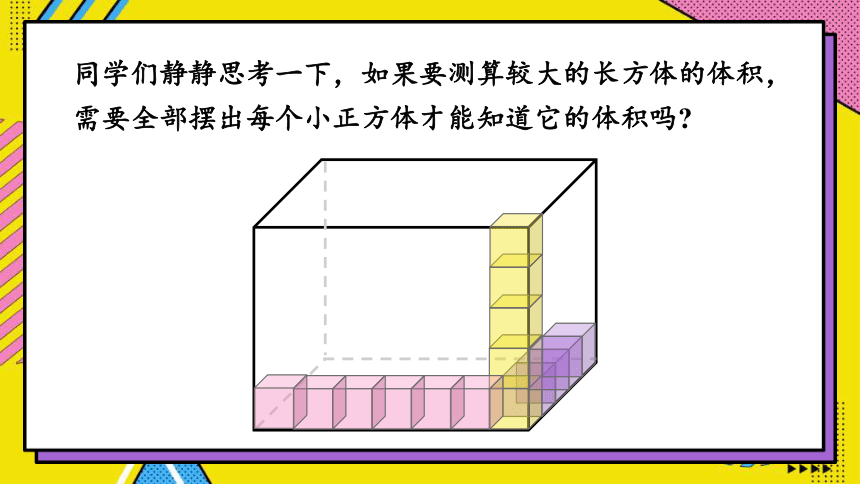
同学们静静思考一下,如果要测算较大的长方体的体积,需要全部摆出每个小正方体才能知道它的体积吗
形状 长 宽 高 小正方体的个数 长方体的体积
12
1
1
12
12
4
3
1
12
12
6
2
1
12
12
3
2
2
12
12
①
②
③
④
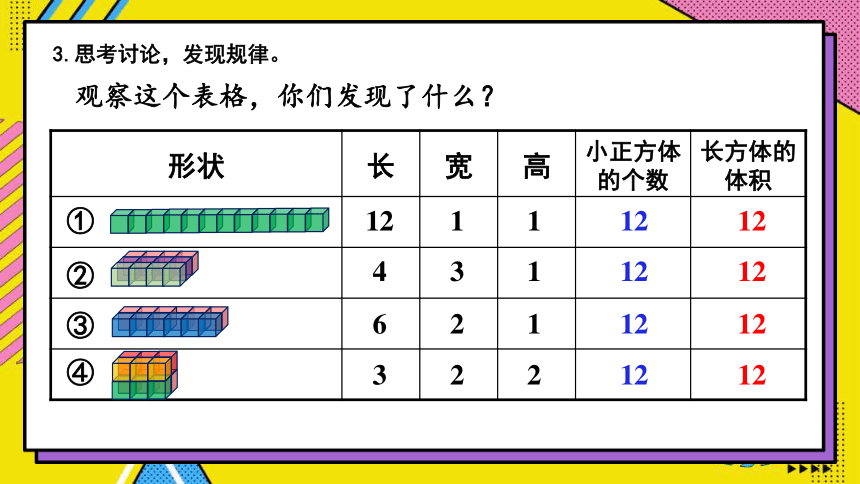
3.思考讨论,发现规律。
观察这个表格,你们发现了什么?
长方体所含体积单位的
个数就是长方体的体积。
长方体的体积 = 每行的个数×行数×层数
长 宽 高
长方体的体积 = × ×
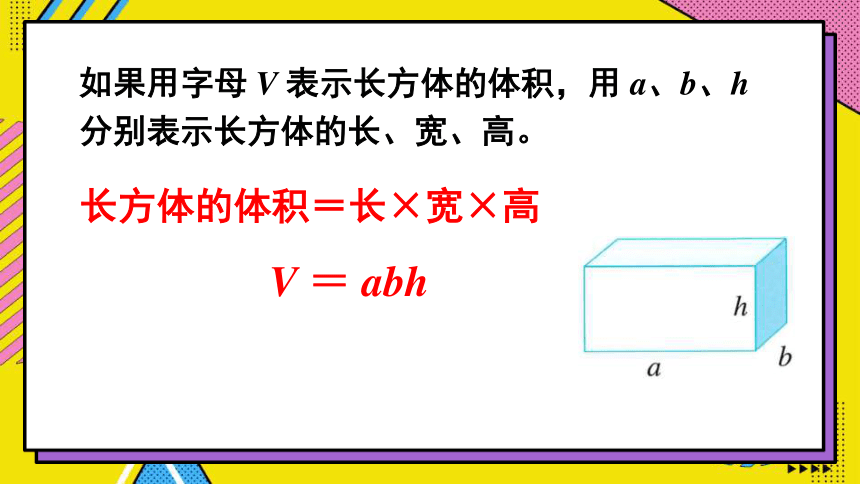
如果用字母 V 表示长方体的体积,用 a、b、h 分别表示长方体的长、宽、高。
长方体的体积=长×宽×高
V = abh
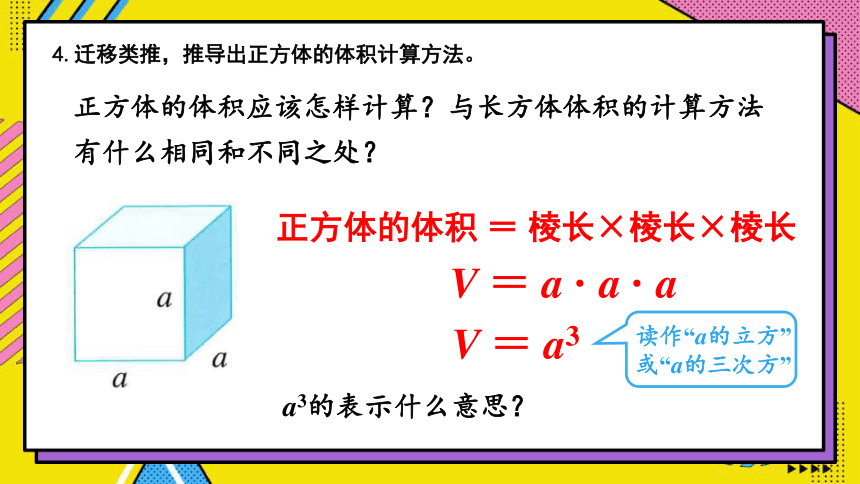
正方体的体积应该怎样计算?与长方体体积的计算方法有什么相同和不同之处?
正方体的体积 = 棱长×棱长×棱长
V = a · a · a
V = a3
4.迁移类推,推导出正方体的体积计算方法。
读作“a的立方”
或“a的三次方”
a3的表示什么意思?
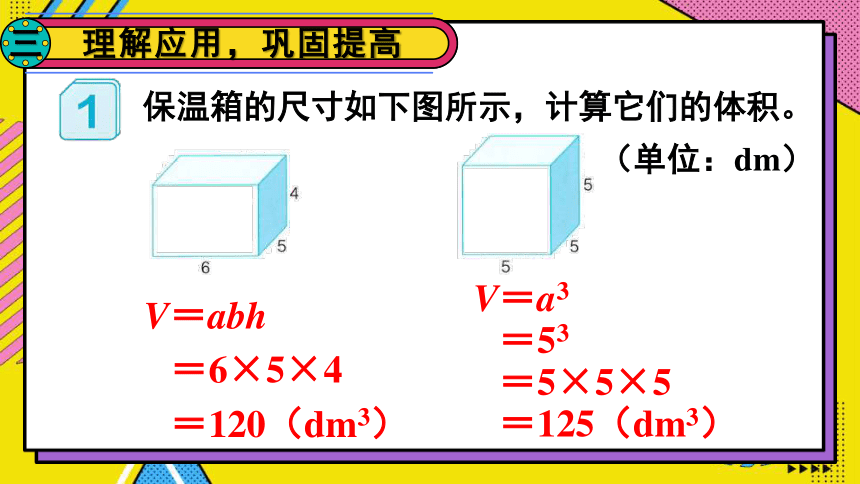
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
V=abh
=6×5×4
=120(dm3)
V=a3
=53
=5×5×5
=125(dm3)
三 理解应用,巩固提高
1.自学教科书 P31 内容,并思考以下问题。
什么叫底面积
长方体和正方体的底面积怎么求
四 深化理解,统一公式
为什么长方体和正方体的体积公式都可以用“底面积×高”来表示 这个公式用字母怎么表示
2.汇报自学收获。
底面
底面
长方体的体积=长×宽×高
底面积
正方体的体积=棱长×棱长×棱长
底面积
长方体(或正方体)的体积=底面积×高
V = Sh
长方体或正方体底面的面积叫作底面积。
一块长方体豆腐的尺寸如下图所示,它的体积是多少?
V=abh
=15×7×5
=525(cm3)
答:它的体积是525cm3。
五 实践应用,内化知识
【选自教材P31 做一做 第1题】
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06m2
长方体体积=底面积×高
选自教材第31页做一做第2题
2
选自教材第31页做一做第1题改编
3
一块长方体肥皂的尺寸如图,它的体积是多少?
15cm
7cm
8cm
长方体体积=长×宽×高
15×7×8=840(cm3)
答:它的体积是840cm3。
计算下面图形的体积。
=15×3×20
=900(cm )
=2.5×2.5×2.5
=15.625(m )
V=abh
V=a
15cm
3cm
20cm
2.5m
2.5m
2.5m
1
一个正方体的棱长总和是108厘米,它的体积是多少?
108÷12=9(厘米)
9×9×9=729(立方厘米)
答:它的体积是729立方厘米。
正方体棱长总和=棱长×12
V=a
2
六 课堂小结
通过这节课的学习,你们对长方体、正方体有了哪些新的认识 计算长方体体积和计算正方体体积有哪些相同和不同之处
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×棱长
V= a3
长方体(或正方体)的体积=底面积×高
V = Sh
这节课有什么收获呢?
长方体(或正方体)的体积=底面积×高
V=abh
S
h
长方体、正方体体积公式的应用
V=a3
V=Sh
七、作业设计
完成课时练本课时内容及以下练习题
一、计算下面各立体图形的体积。
V=abh
=10×4×5
=200(cm3)
V=a3
=7×7×7
=343(m3)
二、把下表中长方体或正方体的相关数据补充完整。
512 m3
15 cm
52 dm2
长方体和正方体的体积
一 情境导入,探索新知
1.什么叫体积?
3.你能比画出1cm3、1dm3、1m3的大小吗?
2.常用的体积单位有哪些?
妈妈要过生日了,淘淘想买一个蛋糕送给妈妈。你知道买哪个蛋糕比较划算吗?
怎样计算两个蛋糕的体积呢?
草莓布朗尼蛋糕
218元
芒果冰激凌慕斯蛋糕
218元
同样的价格,买到的蛋糕越多,也就是蛋糕的体积越大,就越划算!
讨论一下:怎样计算长方体的体积?
求长方体的体积就是看长方体有多少个体积单位。
把长方体分成若干单位体积的小正方体,就可以……
二 动手操作,探究长方体的体积计算方法
1.启发思考。
用 12 个棱长为 1 cm 的小正方体拼摆不同形状的长方体,它们的长、宽、高各是多少?体积又是多少呢?四人一小组,一起动手操作并填写表格。
2.操作实验。
形状 长 宽 高 小正方体的个数 长方体的体积
12
1
1
12
12
4
3
1
12
12
6
2
1
12
12
3
2
2
12
12
①
②
③
④
同学们静静思考一下,如果要测算较大的长方体的体积,需要全部摆出每个小正方体才能知道它的体积吗
形状 长 宽 高 小正方体的个数 长方体的体积
12
1
1
12
12
4
3
1
12
12
6
2
1
12
12
3
2
2
12
12
①
②
③
④
3.思考讨论,发现规律。
观察这个表格,你们发现了什么?
长方体所含体积单位的
个数就是长方体的体积。
长方体的体积 = 每行的个数×行数×层数
长 宽 高
长方体的体积 = × ×
如果用字母 V 表示长方体的体积,用 a、b、h 分别表示长方体的长、宽、高。
长方体的体积=长×宽×高
V = abh
正方体的体积应该怎样计算?与长方体体积的计算方法有什么相同和不同之处?
正方体的体积 = 棱长×棱长×棱长
V = a · a · a
V = a3
4.迁移类推,推导出正方体的体积计算方法。
读作“a的立方”
或“a的三次方”
a3的表示什么意思?
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
V=abh
=6×5×4
=120(dm3)
V=a3
=53
=5×5×5
=125(dm3)
三 理解应用,巩固提高
1.自学教科书 P31 内容,并思考以下问题。
什么叫底面积
长方体和正方体的底面积怎么求
四 深化理解,统一公式
为什么长方体和正方体的体积公式都可以用“底面积×高”来表示 这个公式用字母怎么表示
2.汇报自学收获。
底面
底面
长方体的体积=长×宽×高
底面积
正方体的体积=棱长×棱长×棱长
底面积
长方体(或正方体)的体积=底面积×高
V = Sh
长方体或正方体底面的面积叫作底面积。
一块长方体豆腐的尺寸如下图所示,它的体积是多少?
V=abh
=15×7×5
=525(cm3)
答:它的体积是525cm3。
五 实践应用,内化知识
【选自教材P31 做一做 第1题】
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06m2
长方体体积=底面积×高
选自教材第31页做一做第2题
2
选自教材第31页做一做第1题改编
3
一块长方体肥皂的尺寸如图,它的体积是多少?
15cm
7cm
8cm
长方体体积=长×宽×高
15×7×8=840(cm3)
答:它的体积是840cm3。
计算下面图形的体积。
=15×3×20
=900(cm )
=2.5×2.5×2.5
=15.625(m )
V=abh
V=a
15cm
3cm
20cm
2.5m
2.5m
2.5m
1
一个正方体的棱长总和是108厘米,它的体积是多少?
108÷12=9(厘米)
9×9×9=729(立方厘米)
答:它的体积是729立方厘米。
正方体棱长总和=棱长×12
V=a
2
六 课堂小结
通过这节课的学习,你们对长方体、正方体有了哪些新的认识 计算长方体体积和计算正方体体积有哪些相同和不同之处
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×棱长
V= a3
长方体(或正方体)的体积=底面积×高
V = Sh
这节课有什么收获呢?
长方体(或正方体)的体积=底面积×高
V=abh
S
h
长方体、正方体体积公式的应用
V=a3
V=Sh
七、作业设计
完成课时练本课时内容及以下练习题
一、计算下面各立体图形的体积。
V=abh
=10×4×5
=200(cm3)
V=a3
=7×7×7
=343(m3)
二、把下表中长方体或正方体的相关数据补充完整。
512 m3
15 cm
52 dm2
