2022年湖北省荆门市龙泉中学自主招生数学试题(含答案)
文档属性
| 名称 | 2022年湖北省荆门市龙泉中学自主招生数学试题(含答案) |  | |
| 格式 | Doc | ||
| 文件大小 | 227.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:53:19 | ||
图片预览



文档简介
2022年湖北省荆门市龙泉中学自主招生数学试题
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)若关于x的一元二次方程kx2﹣x+1=0有实数根,则k的取值范围是( )
A.k>且k≠0 B.k<且k≠0 C.k≤且k≠0 D.k<
2.(3分)如图,正方形ABCD在平面直角坐标系中.点A的坐标为(﹣6,4),点B,C在x轴上.将正方形ABCD平移后,点O成为新正方形的对称中心,则正方形ABCD的平移过程可能是( )
A.向右平移6个单位长度,再向下平移4个单位长度
B.向右平移4个单位长度,再向下平移6个单位长度
C.向右平移2个单位长度,再向下平移4个单位长度
D.向右平移4个单位长度,再向下平移2个单位长度
3.(3分)如图,在△BAC中,∠BAC=90°,AB=2AC,将△BAC绕点A顺时针旋转至△DAE,点D刚好落在BC直线上,则△BDE的面积为( )
A. B. C. D.
4.(3分)如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的两倍,则称这样的方程为“2倍根方程”,以下说法不正确的是( )
A.方程x2﹣3x+2=0是2倍根方程
B.若关于x的方程(x﹣2)(mx+n)=0是2倍根方程,则m+n=0
C.若m+n=0且m≠0,则关于x的方程(x﹣2)(mx+n)=0是2倍根方程
D.若2m+n=0且m≠0,则关于x的方程x2+(m﹣n)x﹣mn=0 是2倍根方程
5.(3分)如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是( )
A.△ADC∽△CFB B.AD=DF
C.= D.=
6.(3分)已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.0≤t≤1 B.﹣1≤t≤0 C.﹣5≤t≤4 D.﹣1≤t≤1
7.(3分)如图,在平面直角坐标系中,平行四边形ABCD与y轴分别交于E、F两点,对角线BD在x轴上,反比例函数的图象过点A并交AD于点G,连接DF.若BE:AE=1:2,AG:GD=3:2,且△FCD的面积为,则k的值是( )
A. B.3 C. D.5
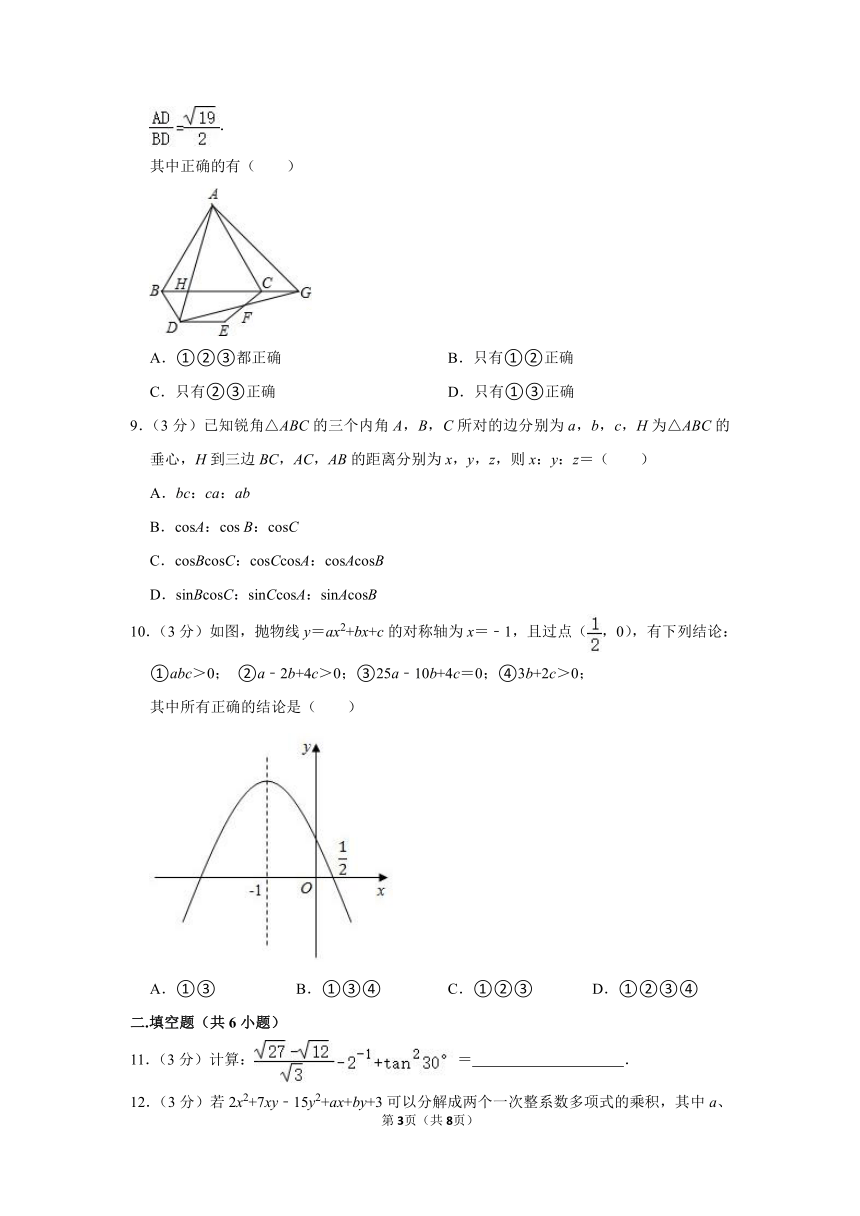
8.(3分)如图,△ABC为等边三角形,BD=DE,∠BDE=120°,连接CE,F为CE的中点,连接DF并延长,连接AD、CG、AG.下列结论:
①CG=DE;②若DE∥BC,则△ABH∽△GBD;③在②的条件下,若CE⊥BC,则.
其中正确的有( )
A.①②③都正确 B.只有①②正确
C.只有②③正确 D.只有①③正确
9.(3分)已知锐角△ABC的三个内角A,B,C所对的边分别为a,b,c,H为△ABC的垂心,H到三边BC,AC,AB的距离分别为x,y,z,则x:y:z=( )
A.bc:ca:ab
B.cosA:cos B:cosC
C.cosBcosC:cosCcosA:cosAcosB
D.sinBcosC:sinCcosA:sinAcosB
10.(3分)如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(,0),有下列结论:
①abc>0; ②a﹣2b+4c>0;③25a﹣10b+4c=0;④3b+2c>0;
其中所有正确的结论是( )
A.①③ B.①③④ C.①②③ D.①②③④
二.填空题(共6小题)
11.(3分)计算:= .
12.(3分)若2x2+7xy﹣15y2+ax+by+3可以分解成两个一次整系数多项式的乘积,其中a、b为整数,那么a+b的最小值是 .
13.(3分)在函数y=+x﹣2中,自变量x的取值范围是 .
14.(3分)如图,A(a,1),B(﹣1,b)都在双曲线y=﹣(x<0)点P,Q分别是x轴,y轴上的动点,当四边形PABQ的周长最小值时,PQ所在直线的解析式是 .
15.(3分)若直线y=m(m为常数)与函数y=的图象有三个不同的交点,则常数m的取值范围 .
16.(3分)如图,在直角坐标系中,直线l1:y=﹣x+与x轴交于点C,与y轴交于点A,分别以OC、OA为边作矩形ABCO,点D、E在直线AC上,且DE=1,则BD+CE的最小值是 .
三.解答题(共8小题)
17.(8分)先化简,再求值:(﹣x+1)÷,其中x是满足﹣1≤x<2的整数.
18.(8分)已知关于x的一元二次方程x2+(2k﹣1)x+k2﹣3=0有实数根.
(ⅰ)求实数k的取值范围;
(ⅱ)当k=2时,方程的根为x1,x2,求代数式(x12+2x1﹣1)(x22+4x2+3)的值.
19.(8分)如图,在直角坐标系中,点A(0,1),点B(3,0),点C(4,3).
(1)判断△ABC的形状并说明理由;
(2)在线段OC的右侧,以OC为边作等腰直角△OCD,点D的坐标为 .
20.(8分)2021年红花岗区某校举办“建党10周年”知识竞赛,成绩分析过程如下:
Ⅰ.收集数据,测试成绩如下:
女生:85 65 80 100 80 75 95 85 80 75
男生:85 100 75 60 85 70 85 60 95 100
Ⅱ.整理、描述数据
60≤x<70 70≤x<80 80≤x<90 90≤x≤100
女生 1 2 a 2
男生 2 2 3 b
Ⅲ.分析数据
平均数 中位数 众数
女生 81.5 c 80
男生 81.5 85 d
根据以上信息,回答下列问题.
(1)a= ,b= ,c= ,d= ;
(2)小明和小颖看到信息后,小颖说:女生成绩较好;小明说:男生成绩较好,你同意 的看法,请说明理由;
(3)该校将从以上20名学生中,筛选出成绩最好的5名学生,随机抽取2名学生参加红花岗区的比赛,求抽到一男一女学生参赛的概率.
21.(8分)如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛40nmile的点A处,它沿着点A的南偏东15°的方向航行.
(1)渔船航行多远距离小岛B最近(结果保留根号)?
(2)渔船到达距离小岛B最近点后,按原航向继续航行20nmile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问救援队从B处出发到达事故地点的最短航程BC是多少nmile(结果保留根号)?
22.(10分)在Rt△ABC中,∠ABC=90°,AB=10,BC=6,以AB为直径作⊙O,点D为直径AB上一动点,连接CD,将线段CD绕点D逆时针旋转90°得到线段ED,连接AE.
(1)如图1,当AD=BC时,求证:AE是⊙O的切线;
(2)如图2,当点E落在⊙O上时,求线段AD的长度;
(3)直接写出点D从点A运动到点B的过程中,点E运动路径的长度.
23.(10分)为了抗击新冠疫情,防疫指挥部计划将甲、乙两厂“生产的防疫物资全部运往A、B两地,甲厂有防疫物资60吨,乙厂有防疫物资40吨,A地需防疫物资70吨,B地需防疫物资30吨,每吨防疫物资的运输费用(百元)见表格,设从甲厂“运往A地防疫物资x吨.
接收地出发地 A地 B地
甲厂 7 10
乙厂 10 15
(1)直接写出x的取值范围: .
(2)请你设计一种调运总费用最低的运输方案,最低费用为多少?
(3)因路况原因,从甲厂到A地的运输费用每吨增加了m百元,从乙厂“到B地的运输费用每吨降低了2m百元,其它每吨运输费用不变,且1≤m≤4,请你探究总运费可以达到的最小值.
24.(12分)如图1,二次函数y=ax2+bx+c的图象交x轴于点A(﹣1,0),B(3,0),交y轴于点C(0,﹣3),直线l经过点B.
(1)求二次函数的表达式和顶点D的坐标;
(2)如图2,当直线l过点D时,求△BCD的面积;
(3)如图3,直线l与抛物线有另一个交点E,且点E使得∠BAC﹣∠CBE>45°,求点E的横坐标m的取值范围;
(4)如图4,动点F在直线l上,作∠CFG=45°,FG与线段AB交于点G,连接CG,当△ABC与△CFG相似,且S△CFG最小时,在直线l上是否存在一点H,使得∠FHG=45°存在,请求出点H的坐标;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.C; 2.D; 3.A; 4.B; 5.C; 6.B; 7.B; 8.A; 9.C; 10.C;
二.填空题(共6小题)
11.; 12.﹣17; 13.x≥﹣4且x≠0; 14.y=x+2; 15.0<m<4; 16.;
三.解答题(共8小题)
17.,1.; 18.(i)k≤;(ii)1.; 19.(3,﹣4),(7,﹣1),(,﹣); 20.5;
3; 80; 85; 小明; 21.(1)渔船航行20nmile距离小岛B最近;
(2)救援队从B处出发到达事故地点的最短航程是40nmile.; 22.(1);(2)7;(3)10.; 23.30≤x≤60; 24.(1)二次函数的表达式为y=x2﹣2x﹣3,顶点D的坐标为(1,﹣4);
(2)S△BCD=3;
(3)点E的横坐标m的取值范围为﹣<m<2;
(4)点H的坐标为:(,)或(,).;
第1页(共1页)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)若关于x的一元二次方程kx2﹣x+1=0有实数根,则k的取值范围是( )
A.k>且k≠0 B.k<且k≠0 C.k≤且k≠0 D.k<
2.(3分)如图,正方形ABCD在平面直角坐标系中.点A的坐标为(﹣6,4),点B,C在x轴上.将正方形ABCD平移后,点O成为新正方形的对称中心,则正方形ABCD的平移过程可能是( )
A.向右平移6个单位长度,再向下平移4个单位长度
B.向右平移4个单位长度,再向下平移6个单位长度
C.向右平移2个单位长度,再向下平移4个单位长度
D.向右平移4个单位长度,再向下平移2个单位长度
3.(3分)如图,在△BAC中,∠BAC=90°,AB=2AC,将△BAC绕点A顺时针旋转至△DAE,点D刚好落在BC直线上,则△BDE的面积为( )
A. B. C. D.
4.(3分)如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的两倍,则称这样的方程为“2倍根方程”,以下说法不正确的是( )
A.方程x2﹣3x+2=0是2倍根方程
B.若关于x的方程(x﹣2)(mx+n)=0是2倍根方程,则m+n=0
C.若m+n=0且m≠0,则关于x的方程(x﹣2)(mx+n)=0是2倍根方程
D.若2m+n=0且m≠0,则关于x的方程x2+(m﹣n)x﹣mn=0 是2倍根方程
5.(3分)如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是( )
A.△ADC∽△CFB B.AD=DF
C.= D.=
6.(3分)已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.0≤t≤1 B.﹣1≤t≤0 C.﹣5≤t≤4 D.﹣1≤t≤1
7.(3分)如图,在平面直角坐标系中,平行四边形ABCD与y轴分别交于E、F两点,对角线BD在x轴上,反比例函数的图象过点A并交AD于点G,连接DF.若BE:AE=1:2,AG:GD=3:2,且△FCD的面积为,则k的值是( )
A. B.3 C. D.5
8.(3分)如图,△ABC为等边三角形,BD=DE,∠BDE=120°,连接CE,F为CE的中点,连接DF并延长,连接AD、CG、AG.下列结论:
①CG=DE;②若DE∥BC,则△ABH∽△GBD;③在②的条件下,若CE⊥BC,则.
其中正确的有( )
A.①②③都正确 B.只有①②正确
C.只有②③正确 D.只有①③正确
9.(3分)已知锐角△ABC的三个内角A,B,C所对的边分别为a,b,c,H为△ABC的垂心,H到三边BC,AC,AB的距离分别为x,y,z,则x:y:z=( )
A.bc:ca:ab
B.cosA:cos B:cosC
C.cosBcosC:cosCcosA:cosAcosB
D.sinBcosC:sinCcosA:sinAcosB
10.(3分)如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(,0),有下列结论:
①abc>0; ②a﹣2b+4c>0;③25a﹣10b+4c=0;④3b+2c>0;
其中所有正确的结论是( )
A.①③ B.①③④ C.①②③ D.①②③④
二.填空题(共6小题)
11.(3分)计算:= .
12.(3分)若2x2+7xy﹣15y2+ax+by+3可以分解成两个一次整系数多项式的乘积,其中a、b为整数,那么a+b的最小值是 .
13.(3分)在函数y=+x﹣2中,自变量x的取值范围是 .
14.(3分)如图,A(a,1),B(﹣1,b)都在双曲线y=﹣(x<0)点P,Q分别是x轴,y轴上的动点,当四边形PABQ的周长最小值时,PQ所在直线的解析式是 .
15.(3分)若直线y=m(m为常数)与函数y=的图象有三个不同的交点,则常数m的取值范围 .
16.(3分)如图,在直角坐标系中,直线l1:y=﹣x+与x轴交于点C,与y轴交于点A,分别以OC、OA为边作矩形ABCO,点D、E在直线AC上,且DE=1,则BD+CE的最小值是 .
三.解答题(共8小题)
17.(8分)先化简,再求值:(﹣x+1)÷,其中x是满足﹣1≤x<2的整数.
18.(8分)已知关于x的一元二次方程x2+(2k﹣1)x+k2﹣3=0有实数根.
(ⅰ)求实数k的取值范围;
(ⅱ)当k=2时,方程的根为x1,x2,求代数式(x12+2x1﹣1)(x22+4x2+3)的值.
19.(8分)如图,在直角坐标系中,点A(0,1),点B(3,0),点C(4,3).
(1)判断△ABC的形状并说明理由;
(2)在线段OC的右侧,以OC为边作等腰直角△OCD,点D的坐标为 .
20.(8分)2021年红花岗区某校举办“建党10周年”知识竞赛,成绩分析过程如下:
Ⅰ.收集数据,测试成绩如下:
女生:85 65 80 100 80 75 95 85 80 75
男生:85 100 75 60 85 70 85 60 95 100
Ⅱ.整理、描述数据
60≤x<70 70≤x<80 80≤x<90 90≤x≤100
女生 1 2 a 2
男生 2 2 3 b
Ⅲ.分析数据
平均数 中位数 众数
女生 81.5 c 80
男生 81.5 85 d
根据以上信息,回答下列问题.
(1)a= ,b= ,c= ,d= ;
(2)小明和小颖看到信息后,小颖说:女生成绩较好;小明说:男生成绩较好,你同意 的看法,请说明理由;
(3)该校将从以上20名学生中,筛选出成绩最好的5名学生,随机抽取2名学生参加红花岗区的比赛,求抽到一男一女学生参赛的概率.
21.(8分)如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛40nmile的点A处,它沿着点A的南偏东15°的方向航行.
(1)渔船航行多远距离小岛B最近(结果保留根号)?
(2)渔船到达距离小岛B最近点后,按原航向继续航行20nmile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问救援队从B处出发到达事故地点的最短航程BC是多少nmile(结果保留根号)?
22.(10分)在Rt△ABC中,∠ABC=90°,AB=10,BC=6,以AB为直径作⊙O,点D为直径AB上一动点,连接CD,将线段CD绕点D逆时针旋转90°得到线段ED,连接AE.
(1)如图1,当AD=BC时,求证:AE是⊙O的切线;
(2)如图2,当点E落在⊙O上时,求线段AD的长度;
(3)直接写出点D从点A运动到点B的过程中,点E运动路径的长度.
23.(10分)为了抗击新冠疫情,防疫指挥部计划将甲、乙两厂“生产的防疫物资全部运往A、B两地,甲厂有防疫物资60吨,乙厂有防疫物资40吨,A地需防疫物资70吨,B地需防疫物资30吨,每吨防疫物资的运输费用(百元)见表格,设从甲厂“运往A地防疫物资x吨.
接收地出发地 A地 B地
甲厂 7 10
乙厂 10 15
(1)直接写出x的取值范围: .
(2)请你设计一种调运总费用最低的运输方案,最低费用为多少?
(3)因路况原因,从甲厂到A地的运输费用每吨增加了m百元,从乙厂“到B地的运输费用每吨降低了2m百元,其它每吨运输费用不变,且1≤m≤4,请你探究总运费可以达到的最小值.
24.(12分)如图1,二次函数y=ax2+bx+c的图象交x轴于点A(﹣1,0),B(3,0),交y轴于点C(0,﹣3),直线l经过点B.
(1)求二次函数的表达式和顶点D的坐标;
(2)如图2,当直线l过点D时,求△BCD的面积;
(3)如图3,直线l与抛物线有另一个交点E,且点E使得∠BAC﹣∠CBE>45°,求点E的横坐标m的取值范围;
(4)如图4,动点F在直线l上,作∠CFG=45°,FG与线段AB交于点G,连接CG,当△ABC与△CFG相似,且S△CFG最小时,在直线l上是否存在一点H,使得∠FHG=45°存在,请求出点H的坐标;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.C; 2.D; 3.A; 4.B; 5.C; 6.B; 7.B; 8.A; 9.C; 10.C;
二.填空题(共6小题)
11.; 12.﹣17; 13.x≥﹣4且x≠0; 14.y=x+2; 15.0<m<4; 16.;
三.解答题(共8小题)
17.,1.; 18.(i)k≤;(ii)1.; 19.(3,﹣4),(7,﹣1),(,﹣); 20.5;
3; 80; 85; 小明; 21.(1)渔船航行20nmile距离小岛B最近;
(2)救援队从B处出发到达事故地点的最短航程是40nmile.; 22.(1);(2)7;(3)10.; 23.30≤x≤60; 24.(1)二次函数的表达式为y=x2﹣2x﹣3,顶点D的坐标为(1,﹣4);
(2)S△BCD=3;
(3)点E的横坐标m的取值范围为﹣<m<2;
(4)点H的坐标为:(,)或(,).;
第1页(共1页)
同课章节目录
