因数和倍数 课件(共24张PPT) 人教版数学五年级下册
文档属性
| 名称 | 因数和倍数 课件(共24张PPT) 人教版数学五年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 19:54:20 | ||
图片预览






文档简介
(共24张PPT)
2 因数与倍数
因数和倍数
温故知新
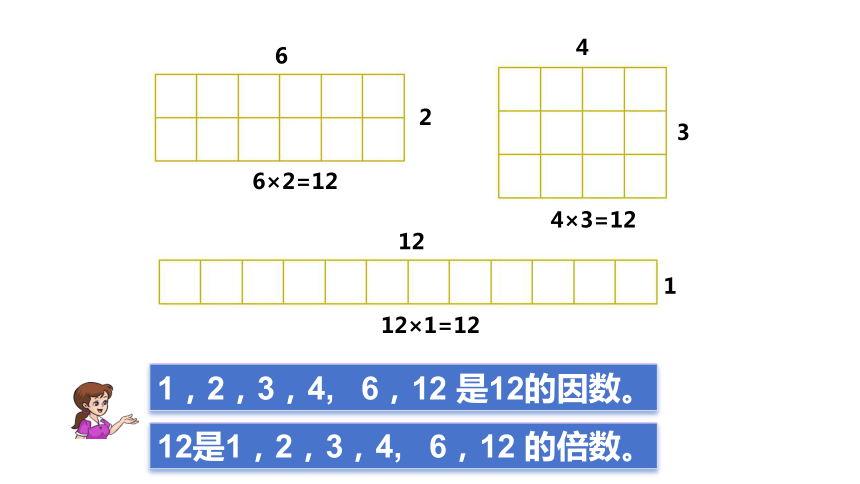
用12个边长是1cm的正方形,可以拼成几种不同形状的长方形?
用12个边长是1cm的正方形,可以拼成几种不同形状的长方形?
4
3
4×3=12
6
2
6×2=12
12
1
12×1=12
1,2,3,4, 6,12 是12的因数。
12是1,2,3,4, 6,12 的倍数。
问题解决
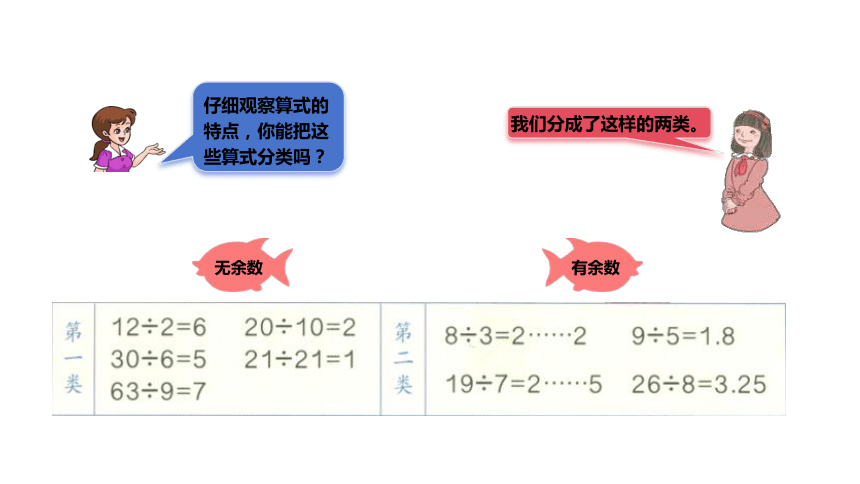
仔细观察算式的特点,你能把这些算式分类吗?
仔细观察算式的特点,你能把这些算式分类吗?
我们分成了这样的两类。
有余数
无余数
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
例如:
12÷2=6,我们就说12是2的倍数,2是12的因数。
12÷6=2,我们就说12是6的倍数,6是12的因数。
为了方便,在研究倍数与因数的时候,我们所说的数指的是自然数(一般不包括0)。
请你在第一类算式中任意选择一个,说一说,谁是谁的因数,谁是谁的倍数?
一、理解因数和倍数的意义
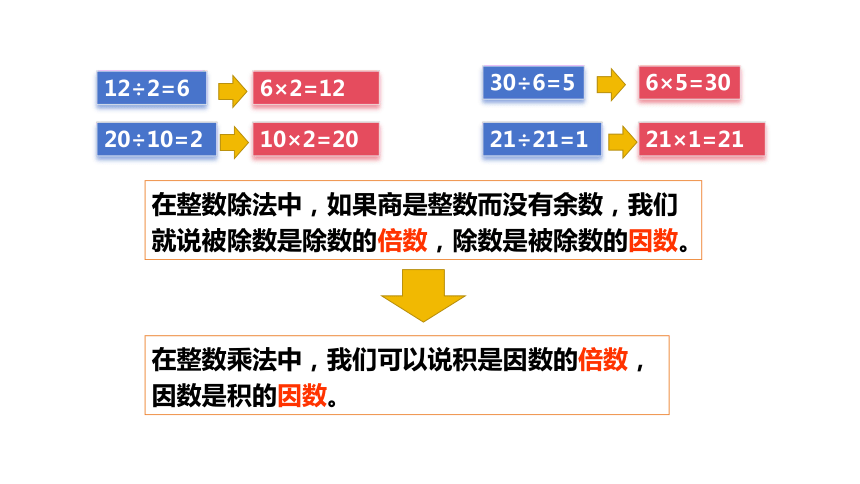
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
12÷2=6
6×2=12
20÷10=2
10×2=20
30÷6=5
6×5=30
21÷21=1
21×1=21
在整数乘法中,我们可以说积是因数的倍数,因数是积的因数。
一、理解因数和倍数的意义
因数和倍数是相互依存的,不是单独存在的。我们不能说4是因数,24是倍数,而应该说4是24的因数,24是4的倍数。
今天学的一个数的“因数”与以前乘法算式中的“因数”有什么区别呢?
因数
因数
积
×
=
0.6
3
1.8
=
×
乘法算式中的“因数”是相对于“积”而言的,可以是整数,也可以是小数、分数。
30÷5=6,那么30是5和6的倍数,5和6是30的因数。
一个数的“因数”是相对于“倍数”而言的,它只能是整数。
乘法算式中的“因数”
一个数的“因数”
想一想,今天学的“倍数”与以前的“倍”又有什么不同呢?
你是怎样找的?
因为18÷1=18,所以1和18是18的因数。
因为18÷2=9,所以2和9是18的因数。
因为18÷3=6,所以3和6是18的因数。
哪两个整数
相乘的积是18?
因为1×18=18,所以1和18是18的因数。
因为2×9=18 ,所以2和9是18的因数。
因为3×6=18 ,所以3和6是18的因数。
可以这样表示:
3
6
9
18
可以这样表示:
3
6
9
18
你能找出30的因数有哪些吗?36的因数呢?
30的因数有:
1,
30
2,
15,
3,
10,
5,
6,
也可以表示成:
30的因数
1, 2, 3, 5,
6,10,15,30
36的因数有:
1,
36
2,
18,
3,
12,
4,
9,
6,
也可以表示成:
1, 2, 3, 4, 6,
9,12,18,36
36的因数
想一想:
怎样找才能不遗漏、不重复地找出一个数的所有因数?
因为2÷2=1,所以2是2的倍数。
因为4÷2=2,所以4是2的倍数。
因为6÷2=3,所以6是2的倍数。
……
因为2×1=2,所以2是2的倍数。
因为2×2=4,所以4是2的倍数。
因为2×3=6,所以6是2的倍数。
……
2的倍数有:
2, 4, 6,…
也可以表示成:
6
8
写得完吗?
你是怎样找的?
你能找出3的倍数有哪些吗?5的倍数呢?
3的倍数有:
3,
…
6,
21
9,
18,
12,
15,
也可以表示成:
3的倍数
3,6,9,12,
15,18,21,…
5的倍数有:
5,
…
10,
25
15,
20,
也可以表示成:
5,10,15,
20,25,…
5的倍数
从前面找因数和倍数的过程中,你有什么发现?
一个数的最小倍数是( )。
一个数最小的因数是( ),最大的因数是( )。
1是所有非零自然数的因数。
一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
1
它本身
它本身
一个数没有最大的倍数。
学以致用
哪些数既是36的因数,也是60的因数?
既是36的因数,又是60的因数的数有:
1, 2, 3, 4, 6, 12
找一个数的因数时,要一对一对地找,避免遗漏。
2. 把5的倍数的星星涂上黄色。
五、巩固练习
5的倍数有什么特点呢?
3.判断
(1)在算式6×4=24中,6是因数,24是倍数。 ( )
(2)15的倍数一定大于15。 ( )
(3)1是除0以外所有自然数的因数。 ( )
(4)40以内6的倍数有12、18、24、30、36这五个( )
(5)一个数的最大因数和它的最小倍数相等。 ( )
×
×
√
×
√
( 6 )34的最小倍数是34,34的最小因数是17。 ( )
( 7 )6既是2的倍数,也是3的倍数。 ( )
×
√
完美数
完美数
6的因数有:1,2,3,6。
完美数
1+2+3=6
1+2+4+7+14=28
28的因数有:1,2,4,
7, 14,28。
完美数
6
28
496
8128
33550336
8589869056
……
毕达哥拉斯
完美数
=1+2+3
=1+2+3+4+5+6+7
稀少而有趣的完美数
任何一个自然数的因数中都有1和它本身,我们把小于它本身的因数叫做这个自然数的真因数。如6的所有真因数是1、2、3,而且6=1+2+3,像这样的数数学家们叫它完美数。
古希腊人非常重视完美数。古希腊著名的数学家毕达哥拉斯发现它之后,人们就开始了对完美数的研究。也许完美数太少了,一直到现在,数学家才发现了29个完美数,而且都是偶完美数。前5个完美数分别是:6, 28, 496, 8128,33550336。
回 顾 反 思
1.静静的想一想,今天学习了什么?
2.我还想到了什么问题?
2 因数与倍数
因数和倍数
温故知新
用12个边长是1cm的正方形,可以拼成几种不同形状的长方形?
用12个边长是1cm的正方形,可以拼成几种不同形状的长方形?
4
3
4×3=12
6
2
6×2=12
12
1
12×1=12
1,2,3,4, 6,12 是12的因数。
12是1,2,3,4, 6,12 的倍数。
问题解决
仔细观察算式的特点,你能把这些算式分类吗?
仔细观察算式的特点,你能把这些算式分类吗?
我们分成了这样的两类。
有余数
无余数
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
例如:
12÷2=6,我们就说12是2的倍数,2是12的因数。
12÷6=2,我们就说12是6的倍数,6是12的因数。
为了方便,在研究倍数与因数的时候,我们所说的数指的是自然数(一般不包括0)。
请你在第一类算式中任意选择一个,说一说,谁是谁的因数,谁是谁的倍数?
一、理解因数和倍数的意义
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
12÷2=6
6×2=12
20÷10=2
10×2=20
30÷6=5
6×5=30
21÷21=1
21×1=21
在整数乘法中,我们可以说积是因数的倍数,因数是积的因数。
一、理解因数和倍数的意义
因数和倍数是相互依存的,不是单独存在的。我们不能说4是因数,24是倍数,而应该说4是24的因数,24是4的倍数。
今天学的一个数的“因数”与以前乘法算式中的“因数”有什么区别呢?
因数
因数
积
×
=
0.6
3
1.8
=
×
乘法算式中的“因数”是相对于“积”而言的,可以是整数,也可以是小数、分数。
30÷5=6,那么30是5和6的倍数,5和6是30的因数。
一个数的“因数”是相对于“倍数”而言的,它只能是整数。
乘法算式中的“因数”
一个数的“因数”
想一想,今天学的“倍数”与以前的“倍”又有什么不同呢?
你是怎样找的?
因为18÷1=18,所以1和18是18的因数。
因为18÷2=9,所以2和9是18的因数。
因为18÷3=6,所以3和6是18的因数。
哪两个整数
相乘的积是18?
因为1×18=18,所以1和18是18的因数。
因为2×9=18 ,所以2和9是18的因数。
因为3×6=18 ,所以3和6是18的因数。
可以这样表示:
3
6
9
18
可以这样表示:
3
6
9
18
你能找出30的因数有哪些吗?36的因数呢?
30的因数有:
1,
30
2,
15,
3,
10,
5,
6,
也可以表示成:
30的因数
1, 2, 3, 5,
6,10,15,30
36的因数有:
1,
36
2,
18,
3,
12,
4,
9,
6,
也可以表示成:
1, 2, 3, 4, 6,
9,12,18,36
36的因数
想一想:
怎样找才能不遗漏、不重复地找出一个数的所有因数?
因为2÷2=1,所以2是2的倍数。
因为4÷2=2,所以4是2的倍数。
因为6÷2=3,所以6是2的倍数。
……
因为2×1=2,所以2是2的倍数。
因为2×2=4,所以4是2的倍数。
因为2×3=6,所以6是2的倍数。
……
2的倍数有:
2, 4, 6,…
也可以表示成:
6
8
写得完吗?
你是怎样找的?
你能找出3的倍数有哪些吗?5的倍数呢?
3的倍数有:
3,
…
6,
21
9,
18,
12,
15,
也可以表示成:
3的倍数
3,6,9,12,
15,18,21,…
5的倍数有:
5,
…
10,
25
15,
20,
也可以表示成:
5,10,15,
20,25,…
5的倍数
从前面找因数和倍数的过程中,你有什么发现?
一个数的最小倍数是( )。
一个数最小的因数是( ),最大的因数是( )。
1是所有非零自然数的因数。
一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
1
它本身
它本身
一个数没有最大的倍数。
学以致用
哪些数既是36的因数,也是60的因数?
既是36的因数,又是60的因数的数有:
1, 2, 3, 4, 6, 12
找一个数的因数时,要一对一对地找,避免遗漏。
2. 把5的倍数的星星涂上黄色。
五、巩固练习
5的倍数有什么特点呢?
3.判断
(1)在算式6×4=24中,6是因数,24是倍数。 ( )
(2)15的倍数一定大于15。 ( )
(3)1是除0以外所有自然数的因数。 ( )
(4)40以内6的倍数有12、18、24、30、36这五个( )
(5)一个数的最大因数和它的最小倍数相等。 ( )
×
×
√
×
√
( 6 )34的最小倍数是34,34的最小因数是17。 ( )
( 7 )6既是2的倍数,也是3的倍数。 ( )
×
√
完美数
完美数
6的因数有:1,2,3,6。
完美数
1+2+3=6
1+2+4+7+14=28
28的因数有:1,2,4,
7, 14,28。
完美数
6
28
496
8128
33550336
8589869056
……
毕达哥拉斯
完美数
=1+2+3
=1+2+3+4+5+6+7
稀少而有趣的完美数
任何一个自然数的因数中都有1和它本身,我们把小于它本身的因数叫做这个自然数的真因数。如6的所有真因数是1、2、3,而且6=1+2+3,像这样的数数学家们叫它完美数。
古希腊人非常重视完美数。古希腊著名的数学家毕达哥拉斯发现它之后,人们就开始了对完美数的研究。也许完美数太少了,一直到现在,数学家才发现了29个完美数,而且都是偶完美数。前5个完美数分别是:6, 28, 496, 8128,33550336。
回 顾 反 思
1.静静的想一想,今天学习了什么?
2.我还想到了什么问题?
