六年级数学下册人教版4.3.8 比例练习十一课件(共25张PPT)
文档属性
| 名称 | 六年级数学下册人教版4.3.8 比例练习十一课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 19:58:40 | ||
图片预览





文档简介
(共25张PPT)
练习十一
第四单元 比例
图形的放大与缩小
把图形按一定的比放大或缩小,就是把图形中各边的长按这样的比放大或缩小,形状不变,大小改变。
图形放大或缩小的倍数是对应边长放大或缩小的倍数。
方格纸上按一定的比将图形各边放大或缩小。
1.数出原图形各边所占的格数。
2.按照放大或缩小的比,算出原图形各边放大或缩小后所占的格数。
(1)设要求的问题为x;
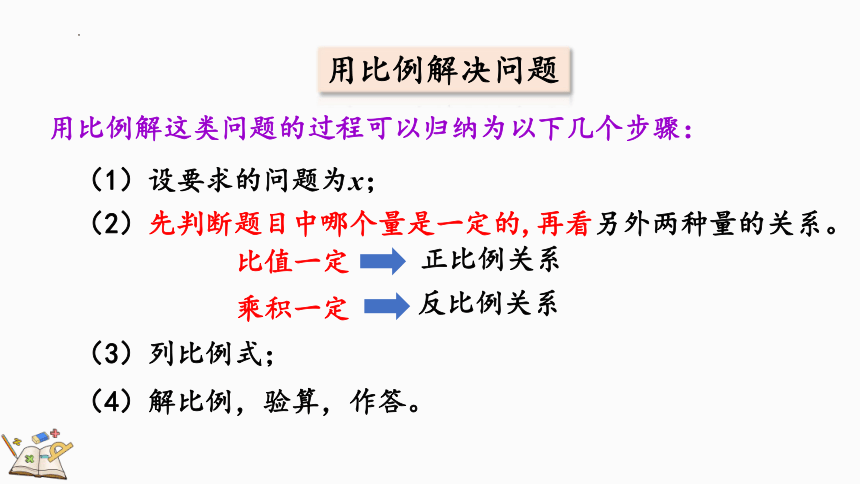
用比例解这类问题的过程可以归纳为以下几个步骤:
用比例解决问题
(3)列比例式;
(2)先判断题目中哪个量是一定的,再看另外两种量的关系。
(4)解比例,验算,作答。
正比例关系
比值一定
反比例关系
乘积一定
1
选自教材第61~62页练习十一
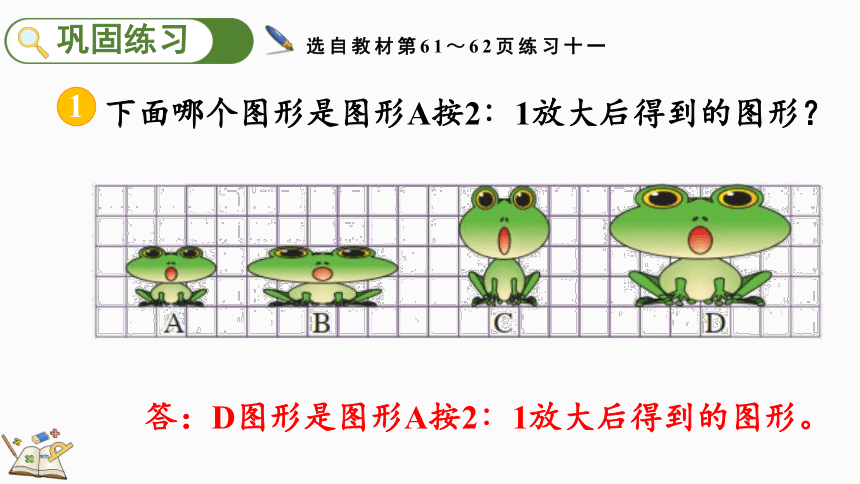
下面哪个图形是图形A按2∶1放大后得到的图形?
答:D图形是图形A按2∶1放大后得到的图形。
2
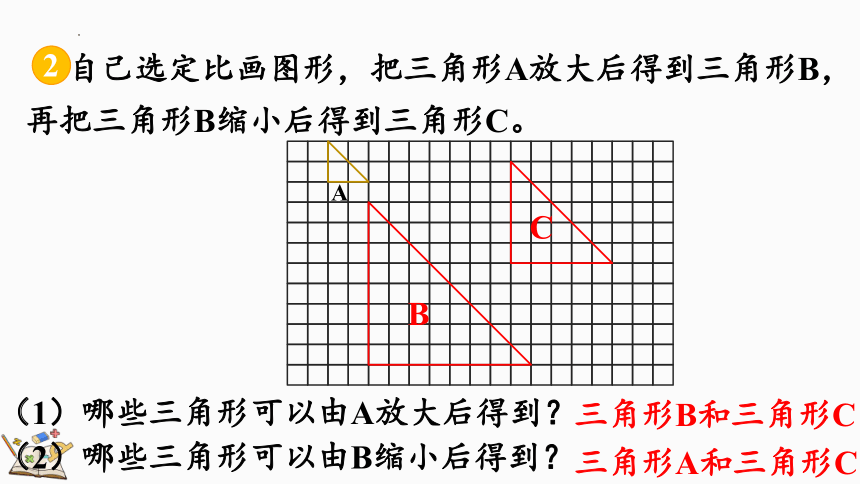
自己选定比画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
A
(1)哪些三角形可以由A放大后得到?
(2)哪些三角形可以由B缩小后得到?
B
C
三角形B和三角形C
三角形A和三角形C
自己选定比画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
(3)*观察三角形A和B,它们的面积有什么变化?面积与边长是按相同的比变化的吗?
三角形A的面积是2×2× =2,
三角形B的面积是8×8× =32。
三角形B的面积是三角形A的面积的32÷2=16倍,面积比是16∶1,
三角形B的边长是三角形A的边长的8÷2=4倍,边长比是4∶1。
所以面积和边长不是按相同的比变化的。
1
2
1
2
2
3
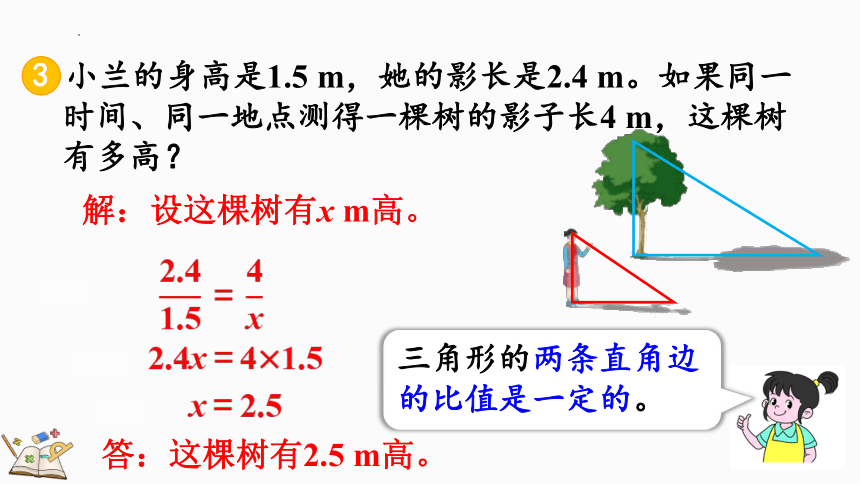
小兰的身高是1.5 m,她的影长是2.4 m。如果同一时间、同一地点测得一棵树的影子长4 m,这棵树有多高?
解:设这棵树有x m高。
答:这棵树有2.5 m高。
三角形的两条直角边的比值是一定的。
4
中国空间站在太空中绕地球运行6周大约需要9小时,运行15周大约要用多长时间?
解:设运行15周大约要用x小时。
答:运行15周大约要用22.5小时。
中国空间站运行的速度是一定的。
5
工程队修一条水渠,每天工作6小时,12天可以完成。如果每小时的工作量不变,每天工作8小时,多少天可以完成任务?
解:设x天可以完成任务。
8x=6×12
x=9
答:9天可以完成任务。
6
甲、乙两地之间的高速铁路大约长1600 km。丙地在甲地、乙地之间,甲地到丙地的高速铁路大约长700 km。一列由甲地开往乙地的高速列车,9:00出发,11:30到达丙地。按照这样的平均速度,6小时能从甲地到乙地吗?
解:设从甲地到乙地需要x小时。
答: 6小时能从甲地到乙地。
速度一定
9:00到11:30经过了2.5小时。
=
= 5
5 < 6
7
一列货车运送物资,2小时行驶了160km。按照这样的速度,驶完400km需要多少小时?
解:设驶完400km需要 x 小时。
400∶x=160∶2
x=5
答:驶完400km需要5小时。
8
小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?
解:设平均每天要读x页。
30×8=6x
x=40
答:平均每天要读40页。
9
用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(1)现在想用30小时收割完,那么每小时应收割多少公顷?
解:设每小时应收割x公顷。
30x=0.3×40
x=0.4
答:每小时应收割0.4公顷。
9
用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(2)每公顷产小麦8t,这块地一共产小麦多少吨?
8×(0.3×40)=96(t)
答:这块地一共产小麦96t。
9
用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(3)你能提出其他数学问题并解答吗?
如果想用20小时收割完,那么每小时应收割多少公顷?
解:设每小时应收割y公顷。
20y=0.3×40
y=0.6
答:每小时应收割0.6公顷。
10
一辆运货汽车从甲地到乙地,平均每小时行驶72km,10小时到达。回来时空车原路返回,每小时可行驶90km,多长时间能够返回甲地?
解:设x小时能够返回甲地。
90x=72×10
x=8
答:8小时能够返回甲地。
11
小芳的姐姐在上大学,妈妈每个月(按30天算)按每天40元的标准给她一笔生活费。
(1)如果姐姐每天花30元,一个月的生活费够花多少天?
解:设一个月的生活费够花x天。
30x=40×30
x=40
答:一个月的生活费够花40天。
11
小芳的姐姐在上大学,妈妈每个月(按30天算)按每天40元的标准给她一笔生活费。
(2)如果一个月的生活费姐姐花了32天,平均每天花多少钱?
解:设平均每天花x元钱。
32x=40×30
x=37.5
答:平均每天花37.5元。
12
小东家的客厅是正方形的,用边长0.6m的方砖铺地,正好需要100块。如果改用边长0.5m的方砖铺地,需要多少块?
解:设需要x块。
0.5 x=0.6 ×100
x=144
答:需要144块。
1.按4∶1画出下面图形放大后的图形,然后按1∶2缩小。
2.在下图中按3∶1把圆放大,按1∶2把梯形缩小。
3.在括号里填上“成正比例”“成反比例”或“不成比例”。
(1)班级人数一定 ,每组人数和分的组数。( )
(2)正方体的棱长与它的棱长总和。 ( )
(3)小强家的收入一定,他家的支出与结余。( )
成反比例
成正比例
不成比例
(4)圆锥的体积一定,它的底面积和高。 ( )
成反比例
支出+结余=收入(一定)
每组人数×分的组数=总人数(一定)
正方体的棱长总和÷棱长=12(一定)
4.如果500千克海水能晒制15千克盐,那么引入24500千克海水到盐田,可以制成多少吨盐?
解:可以制成x千克盐。
15∶500=x∶24500
x=735
答:可以制成0.735吨盐。
735千克=0.735吨
这节课有什么收获呢?
灵活运用正、反比例知识解决实际问题:
若相关的量的乘积一定,用反比例解决问题;
若相关的量的比值一定,用正比例解决问题。
练习十一
若相关的量的乘积一定,用反比例解决问题;
若相关的量的比值一定,用正比例解决问题。
练习十一
第四单元 比例
图形的放大与缩小
把图形按一定的比放大或缩小,就是把图形中各边的长按这样的比放大或缩小,形状不变,大小改变。
图形放大或缩小的倍数是对应边长放大或缩小的倍数。
方格纸上按一定的比将图形各边放大或缩小。
1.数出原图形各边所占的格数。
2.按照放大或缩小的比,算出原图形各边放大或缩小后所占的格数。
(1)设要求的问题为x;
用比例解这类问题的过程可以归纳为以下几个步骤:
用比例解决问题
(3)列比例式;
(2)先判断题目中哪个量是一定的,再看另外两种量的关系。
(4)解比例,验算,作答。
正比例关系
比值一定
反比例关系
乘积一定
1
选自教材第61~62页练习十一
下面哪个图形是图形A按2∶1放大后得到的图形?
答:D图形是图形A按2∶1放大后得到的图形。
2
自己选定比画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
A
(1)哪些三角形可以由A放大后得到?
(2)哪些三角形可以由B缩小后得到?
B
C
三角形B和三角形C
三角形A和三角形C
自己选定比画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
(3)*观察三角形A和B,它们的面积有什么变化?面积与边长是按相同的比变化的吗?
三角形A的面积是2×2× =2,
三角形B的面积是8×8× =32。
三角形B的面积是三角形A的面积的32÷2=16倍,面积比是16∶1,
三角形B的边长是三角形A的边长的8÷2=4倍,边长比是4∶1。
所以面积和边长不是按相同的比变化的。
1
2
1
2
2
3
小兰的身高是1.5 m,她的影长是2.4 m。如果同一时间、同一地点测得一棵树的影子长4 m,这棵树有多高?
解:设这棵树有x m高。
答:这棵树有2.5 m高。
三角形的两条直角边的比值是一定的。
4
中国空间站在太空中绕地球运行6周大约需要9小时,运行15周大约要用多长时间?
解:设运行15周大约要用x小时。
答:运行15周大约要用22.5小时。
中国空间站运行的速度是一定的。
5
工程队修一条水渠,每天工作6小时,12天可以完成。如果每小时的工作量不变,每天工作8小时,多少天可以完成任务?
解:设x天可以完成任务。
8x=6×12
x=9
答:9天可以完成任务。
6
甲、乙两地之间的高速铁路大约长1600 km。丙地在甲地、乙地之间,甲地到丙地的高速铁路大约长700 km。一列由甲地开往乙地的高速列车,9:00出发,11:30到达丙地。按照这样的平均速度,6小时能从甲地到乙地吗?
解:设从甲地到乙地需要x小时。
答: 6小时能从甲地到乙地。
速度一定
9:00到11:30经过了2.5小时。
=
= 5
5 < 6
7
一列货车运送物资,2小时行驶了160km。按照这样的速度,驶完400km需要多少小时?
解:设驶完400km需要 x 小时。
400∶x=160∶2
x=5
答:驶完400km需要5小时。
8
小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?
解:设平均每天要读x页。
30×8=6x
x=40
答:平均每天要读40页。
9
用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(1)现在想用30小时收割完,那么每小时应收割多少公顷?
解:设每小时应收割x公顷。
30x=0.3×40
x=0.4
答:每小时应收割0.4公顷。
9
用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(2)每公顷产小麦8t,这块地一共产小麦多少吨?
8×(0.3×40)=96(t)
答:这块地一共产小麦96t。
9
用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
(3)你能提出其他数学问题并解答吗?
如果想用20小时收割完,那么每小时应收割多少公顷?
解:设每小时应收割y公顷。
20y=0.3×40
y=0.6
答:每小时应收割0.6公顷。
10
一辆运货汽车从甲地到乙地,平均每小时行驶72km,10小时到达。回来时空车原路返回,每小时可行驶90km,多长时间能够返回甲地?
解:设x小时能够返回甲地。
90x=72×10
x=8
答:8小时能够返回甲地。
11
小芳的姐姐在上大学,妈妈每个月(按30天算)按每天40元的标准给她一笔生活费。
(1)如果姐姐每天花30元,一个月的生活费够花多少天?
解:设一个月的生活费够花x天。
30x=40×30
x=40
答:一个月的生活费够花40天。
11
小芳的姐姐在上大学,妈妈每个月(按30天算)按每天40元的标准给她一笔生活费。
(2)如果一个月的生活费姐姐花了32天,平均每天花多少钱?
解:设平均每天花x元钱。
32x=40×30
x=37.5
答:平均每天花37.5元。
12
小东家的客厅是正方形的,用边长0.6m的方砖铺地,正好需要100块。如果改用边长0.5m的方砖铺地,需要多少块?
解:设需要x块。
0.5 x=0.6 ×100
x=144
答:需要144块。
1.按4∶1画出下面图形放大后的图形,然后按1∶2缩小。
2.在下图中按3∶1把圆放大,按1∶2把梯形缩小。
3.在括号里填上“成正比例”“成反比例”或“不成比例”。
(1)班级人数一定 ,每组人数和分的组数。( )
(2)正方体的棱长与它的棱长总和。 ( )
(3)小强家的收入一定,他家的支出与结余。( )
成反比例
成正比例
不成比例
(4)圆锥的体积一定,它的底面积和高。 ( )
成反比例
支出+结余=收入(一定)
每组人数×分的组数=总人数(一定)
正方体的棱长总和÷棱长=12(一定)
4.如果500千克海水能晒制15千克盐,那么引入24500千克海水到盐田,可以制成多少吨盐?
解:可以制成x千克盐。
15∶500=x∶24500
x=735
答:可以制成0.735吨盐。
735千克=0.735吨
这节课有什么收获呢?
灵活运用正、反比例知识解决实际问题:
若相关的量的乘积一定,用反比例解决问题;
若相关的量的比值一定,用正比例解决问题。
练习十一
若相关的量的乘积一定,用反比例解决问题;
若相关的量的比值一定,用正比例解决问题。
