三角形全等的条件(2)(湖北省荆门市)
文档属性
| 名称 | 三角形全等的条件(2)(湖北省荆门市) |  | |
| 格式 | rar | ||
| 文件大小 | 700.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-30 20:48:00 | ||
图片预览


文档简介
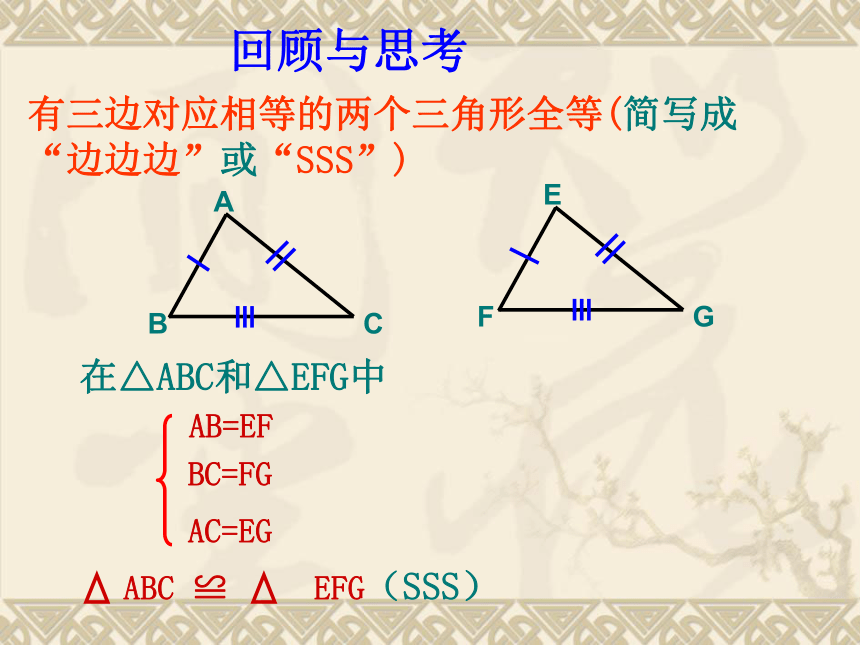
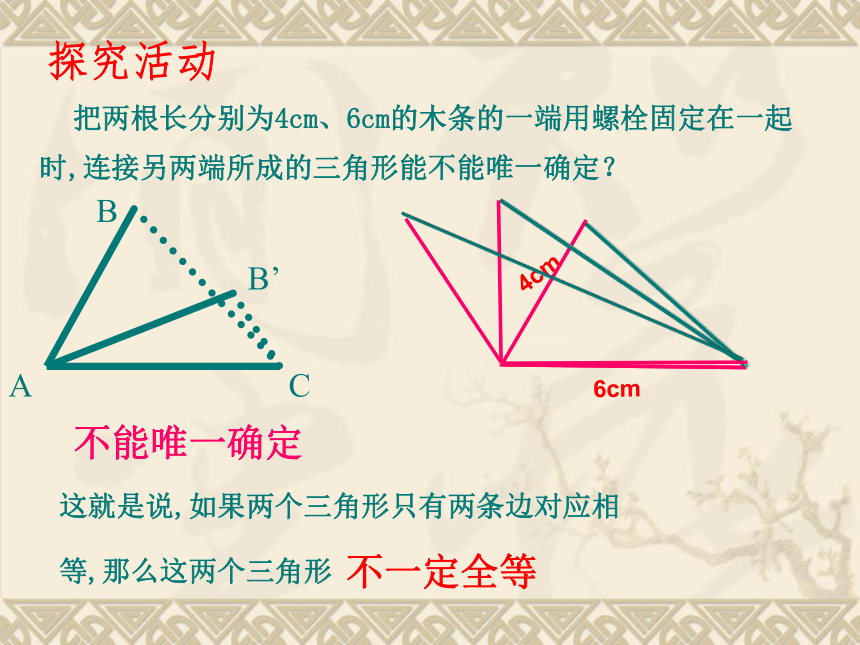
课件18张PPT。宋河二中 史林森三角形全等的条(2)AB=EFBC=FGAC=EG(SSS)有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)在△ABC和△EFG中回顾与思考探究活动 把两根长分别为4cm、6cm的木条的一端用螺栓固定在一起时,连接另两端所成的三角形能不能唯一确定?这就是说,如果两个三角形只有两条边对应相
等,那么这两个三角形
不能唯一确定不一定全等 用量角器和刻度尺画△ABC,使AB=4cm,BC=6cm,∠ABC=600。画法:2、在射线BM上截取AB=4cm;3、在射线BN上截取BC=6cm;1、∠MBN=60°;4、连接AC则△ABC就是所求的三角形
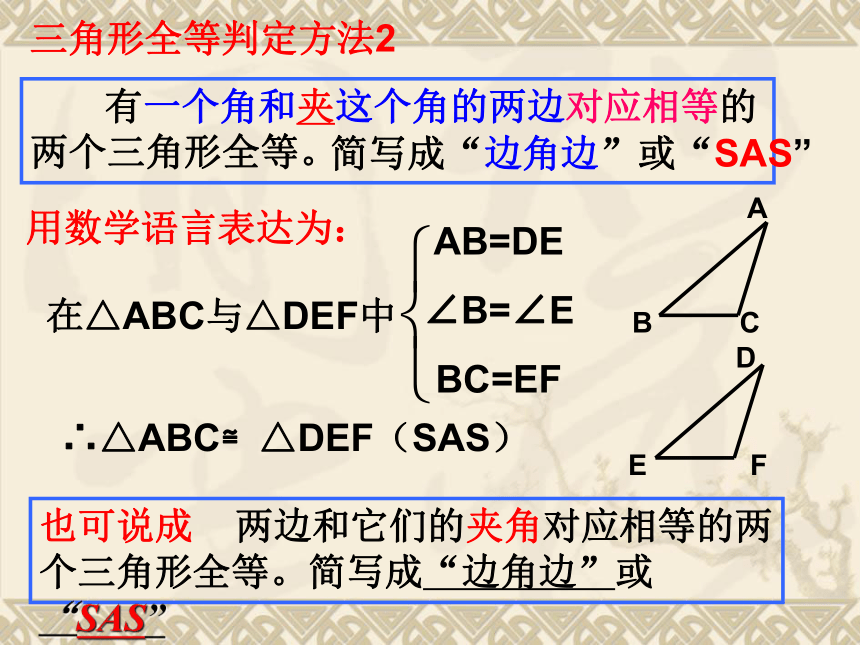
有两边和一个角对应相等的两个三角形全等吗?合作学习把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?想一想:BMANC三角形全等判定方法2用数学语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
BC=EF∴△ABC≌△DEF(SAS) 有一个角和夹这个角的两边对应相等的两个三角形全等。简写成“边角边”或“SAS”也可说成 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”在△ABC和△DEF中AB=DE
_____=______
BC=EF ∴△ABC≌△DEF(SAS)∠B ∠C____=____
∠C=∠F
____=____BC EFAC DF填一填想一想: 星期天,小刚在家玩蓝球,不小心将一块三角形玻璃摔坏了(如图所示)。情急之中,小刚量出了AB、BC的长,然后便去了玻璃店,他想重新裁得一块和原来一样的三角形玻璃。小刚能如愿吗?辨一辨在下列图中找出全等三角形,并把它们用符号写出来.ⅠⅡⅢⅣⅤⅥⅦⅧ30o???30o30o???30o30o30oⅣⅧ8888888899885555全等三角形有:Ⅰ与Ⅲ ,Ⅱ与Ⅴ ,Ⅳ与Ⅷ ,Ⅵ与 Ⅶ 。补充训练题:ABCDEF1)如果AB = ED,∠B = ∠D, ,
则?ABC ≌ ?EDF2)如果BC = DF, ,AC = EF则?BAC ≌ ; 3)如果 ,∠A = ∠E,AB = ED
则 ≌ ?FED = 或? =?填一填: 在下面的图中,有①、②、③三个三角形,根据
图中条件,三角形_____和_____全等(填序号即可)①②注意:已知两边时,这个角一定要是这两边所夹的角。例1: 如图,AC与BD相交于点O。已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
在△AOB和△COD中
OA=OC,
∠AOB=∠COD
OB=OD
∴ △AOB≌△COD(SAS) 解:∵ AC与BD相交于点O
∴ ∠AOB=∠COD(对顶角相等)归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。做一做:如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。解:连结AA’,BB’,AB,A’B’∵点O是AA’,BB’的中点
∴ A’O=AO,B’O=BO∵ 在△AOB和△A’OB’中
OA=OA’,
∠AOB=∠ A’OB’
OB=OB’
∴ △AOB≌△ A’OB’ (SAS)
∴ AB=A’B’ (全等三角形的对应边等)例2 已知:如图,AD与BE交于F,AF=BF, ∠1=∠2.
求证:AC=BC
证明:∵ ∠AFE=∠BFD (对顶角相等)又∵ ∠1=∠2 ∴∠AFE+∠1=∠BFD+∠2 (等式性质) 即 ∠AFC=∠BFC 在△AFC与△BFC中 AF=BF (已知) ∠AFC=∠BFC (已证) CF=CF (公共边) ∴ △AFC≌△BFC (SAS) ∴ AC=BC (全等三角形的对应边相等) △AFC△BFC≌小结 与你同桌交流一下,然后请说一说,你本节课学习了些什么?2. 用尺规作图,已知三角形两边与夹角求作三角形3. SAS的应用1. 三角形全等的判定方法二,有一个角和夹这个角的两边也对应相等的两个三角形全等(边角边或SAS)1、已知AB=DE, AC=DF, 要说明△ABC≌△DEF,
还需增加一个什么条件?做一做:BE=CFBC=EF
或BE=CF
或∠A=∠D求:∠DBE的度数.
?
?
?
B
2、 如图,A、B、C三点在一条直线上,DA⊥AC,EC⊥AC,AB=CE,AD=CB.
?
?
3、 如图,A、B、C三点在一条直线上,AD=AE,AC平分∠DAE,图中有多少对全等三角形?证明你的结论.
4、如图池塘两端A、B无法直接达到,因此这两点的距离无法直接量出。
ABCED提示:任取一点C连结AC、BC延长AC至D使CD=CA延长BC至E使EC=BC连结ED这样只要量出ED的长就是AB的长。为什么?做一做?已知:点A、E、F、C在同一条直线上, AD=CB,AD∥CB,AE=CF. 求证:EB∥DF
ADBCEF证明:∵ AD∥CB(已知)∴ ∠A=∠C ∵ AE=CF (已知)∴ AE+EF=CF+EF 即 AF=CE在△AFD与△CEB中AF=CE (已证)∠A=∠C (已证)AD=CB( 已知)∴∴△AFD ≌ △CEB(SAS)∴ ∠AFD=∠CEB∴ EB∥DF
等,那么这两个三角形
不能唯一确定不一定全等 用量角器和刻度尺画△ABC,使AB=4cm,BC=6cm,∠ABC=600。画法:2、在射线BM上截取AB=4cm;3、在射线BN上截取BC=6cm;1、∠MBN=60°;4、连接AC则△ABC就是所求的三角形
有两边和一个角对应相等的两个三角形全等吗?合作学习把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?想一想:BMANC三角形全等判定方法2用数学语言表达为:在△ABC与△DEF中AB=DE
∠B=∠E
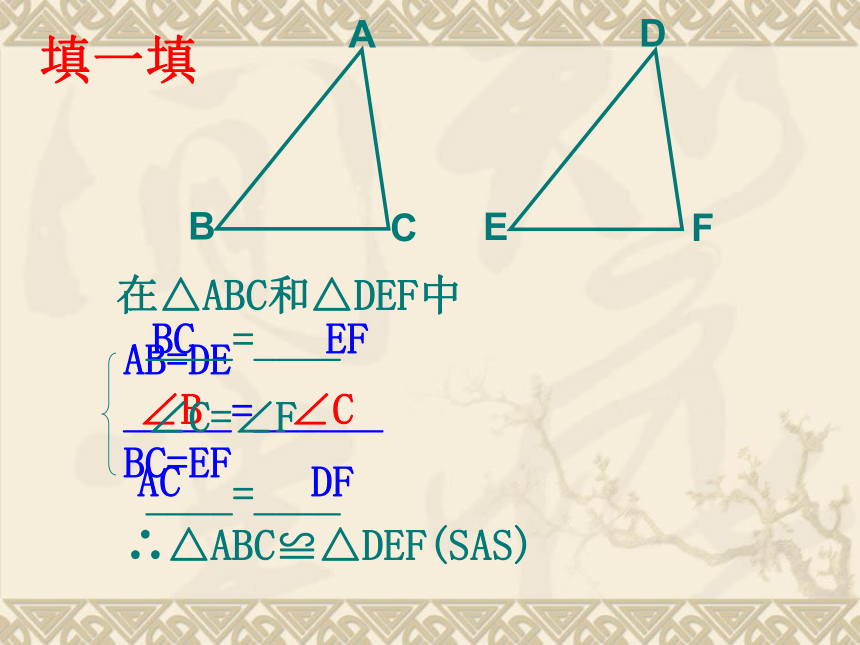
BC=EF∴△ABC≌△DEF(SAS) 有一个角和夹这个角的两边对应相等的两个三角形全等。简写成“边角边”或“SAS”也可说成 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”在△ABC和△DEF中AB=DE
_____=______
BC=EF ∴△ABC≌△DEF(SAS)∠B ∠C____=____
∠C=∠F
____=____BC EFAC DF填一填想一想: 星期天,小刚在家玩蓝球,不小心将一块三角形玻璃摔坏了(如图所示)。情急之中,小刚量出了AB、BC的长,然后便去了玻璃店,他想重新裁得一块和原来一样的三角形玻璃。小刚能如愿吗?辨一辨在下列图中找出全等三角形,并把它们用符号写出来.ⅠⅡⅢⅣⅤⅥⅦⅧ30o???30o30o???30o30o30oⅣⅧ8888888899885555全等三角形有:Ⅰ与Ⅲ ,Ⅱ与Ⅴ ,Ⅳ与Ⅷ ,Ⅵ与 Ⅶ 。补充训练题:ABCDEF1)如果AB = ED,∠B = ∠D, ,
则?ABC ≌ ?EDF2)如果BC = DF, ,AC = EF则?BAC ≌ ; 3)如果 ,∠A = ∠E,AB = ED
则 ≌ ?FED = 或? =?填一填: 在下面的图中,有①、②、③三个三角形,根据
图中条件,三角形_____和_____全等(填序号即可)①②注意:已知两边时,这个角一定要是这两边所夹的角。例1: 如图,AC与BD相交于点O。已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
在△AOB和△COD中
OA=OC,
∠AOB=∠COD
OB=OD
∴ △AOB≌△COD(SAS) 解:∵ AC与BD相交于点O
∴ ∠AOB=∠COD(对顶角相等)归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。做一做:如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。解:连结AA’,BB’,AB,A’B’∵点O是AA’,BB’的中点
∴ A’O=AO,B’O=BO∵ 在△AOB和△A’OB’中
OA=OA’,
∠AOB=∠ A’OB’
OB=OB’
∴ △AOB≌△ A’OB’ (SAS)
∴ AB=A’B’ (全等三角形的对应边等)例2 已知:如图,AD与BE交于F,AF=BF, ∠1=∠2.
求证:AC=BC
证明:∵ ∠AFE=∠BFD (对顶角相等)又∵ ∠1=∠2 ∴∠AFE+∠1=∠BFD+∠2 (等式性质) 即 ∠AFC=∠BFC 在△AFC与△BFC中 AF=BF (已知) ∠AFC=∠BFC (已证) CF=CF (公共边) ∴ △AFC≌△BFC (SAS) ∴ AC=BC (全等三角形的对应边相等) △AFC△BFC≌小结 与你同桌交流一下,然后请说一说,你本节课学习了些什么?2. 用尺规作图,已知三角形两边与夹角求作三角形3. SAS的应用1. 三角形全等的判定方法二,有一个角和夹这个角的两边也对应相等的两个三角形全等(边角边或SAS)1、已知AB=DE, AC=DF, 要说明△ABC≌△DEF,
还需增加一个什么条件?做一做:BE=CFBC=EF
或BE=CF
或∠A=∠D求:∠DBE的度数.
?
?
?
B
2、 如图,A、B、C三点在一条直线上,DA⊥AC,EC⊥AC,AB=CE,AD=CB.
?
?
3、 如图,A、B、C三点在一条直线上,AD=AE,AC平分∠DAE,图中有多少对全等三角形?证明你的结论.
4、如图池塘两端A、B无法直接达到,因此这两点的距离无法直接量出。
ABCED提示:任取一点C连结AC、BC延长AC至D使CD=CA延长BC至E使EC=BC连结ED这样只要量出ED的长就是AB的长。为什么?做一做?已知:点A、E、F、C在同一条直线上, AD=CB,AD∥CB,AE=CF. 求证:EB∥DF
ADBCEF证明:∵ AD∥CB(已知)∴ ∠A=∠C ∵ AE=CF (已知)∴ AE+EF=CF+EF 即 AF=CE在△AFD与△CEB中AF=CE (已证)∠A=∠C (已证)AD=CB( 已知)∴∴△AFD ≌ △CEB(SAS)∴ ∠AFD=∠CEB∴ EB∥DF
