数列说课(浙江省杭州市桐庐县)
文档属性
| 名称 | 数列说课(浙江省杭州市桐庐县) |  | |
| 格式 | rar | ||
| 文件大小 | 873.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-28 19:23:00 | ||
图片预览




文档简介
课件25张PPT。 桐庐中学: 包梅芳数列说课教材分析目标分析教学方法教学过程说明反思 教材分析教材的地位和作用 教材分析 课时安排和说明教学的重点和难点(一)教材的地位与作用 “数列”这节课的教学内容是高一数学第三章《数列》的 第一节,是开启课。
数列是高中数学的重要内容之一,它的地位作用可以从三个方面来看:
(1)数列有着广泛的实际应用。如堆放物品总数的计算要用到数列前n项和公式;又如产品规格设计的某些问题要用到等比数列的原理;再如储蓄、分期付款的有关计算也要用到数列的一些知识。
(2)数列起着承前启后的作用。一方面,初中数学的许多内容在解决数列的某些问题中得到了充分运用,数列与前面学习的函数等知识有密切的联系;数列是刻画离散现象的函数,是一种重要的数学模型,人们往往通过离散现象认识连续现象.另一方面,学习数列又为进一步学习数列的极限等内容作好了准备。因此就有必要研究数列。
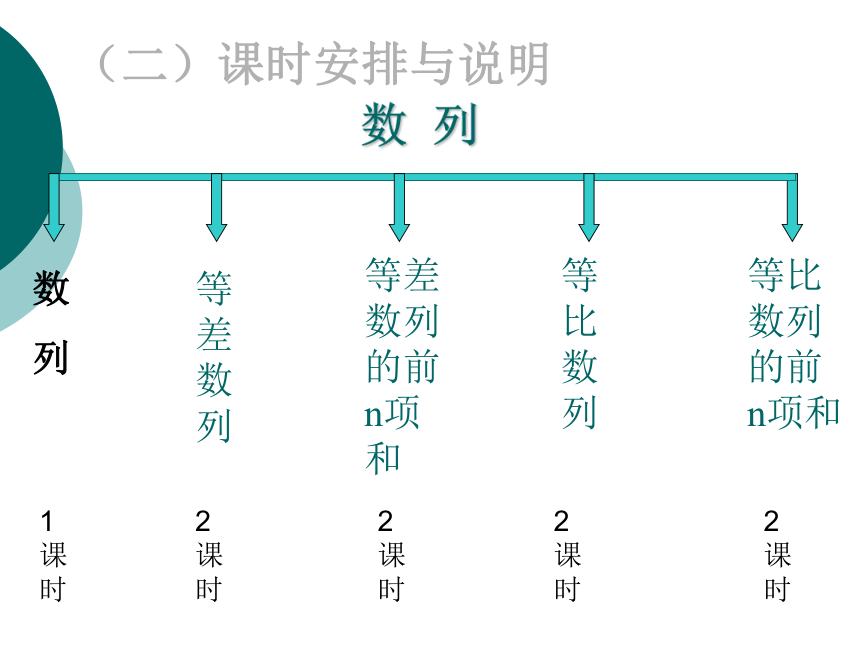
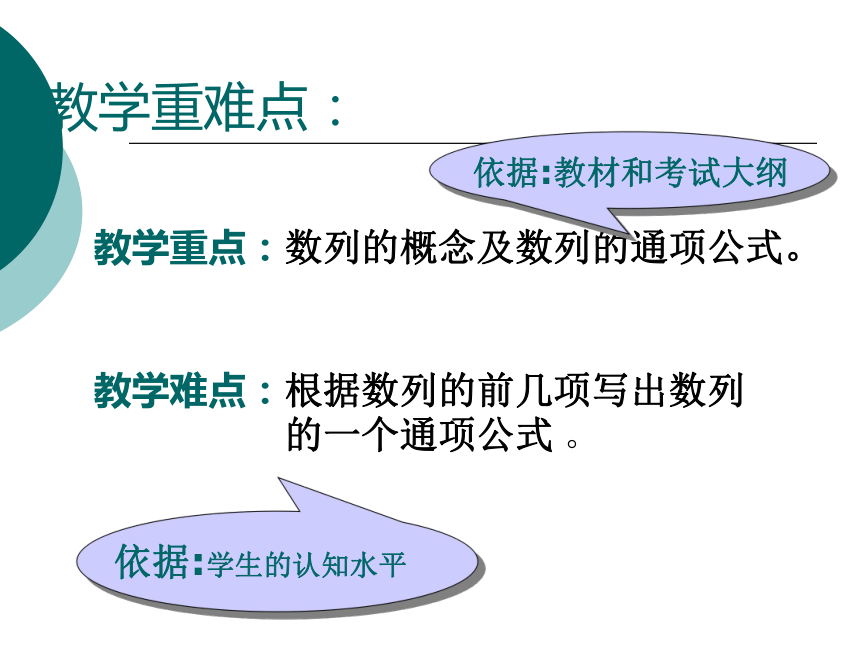
(3)数列是培养学生数学能力的良好题材。学习数列,要经常观察、分析、归纳、猜想,还要综合运用前面的知识解决数列中的一些问题,这些都有助于学生数学能力的提高。(二)课时安排与说明 教学重难点: 教学重点:数列的概念及数列的通项公式。
教学难点:根据数列的前几项写出数列
的一个通项公式 。
依据:学生的认知水平依据:教材和考试大纲一、知识目标:通过枚举归纳:
?① 认识数列的特点,掌握数列的概念及表示方法。
?②?了解数列通项公式的意义及数列分类。
?③能由数列的通项公式求出数列的各项,反之, 能由数列的前几项写出数列的 一个通项公式。
二、能力目标:通过对数列通项公式的探究和应用,帮助学生通过问题解决获得数学知识;在交流过程中,养成表述、抽象、类比、概括、总结的思维习惯。
三、情感目标:通过各种有趣的,贴近学生生活的素材激发学生的学习兴趣和热爱生活的情感。
二、说教法 根据《教学大纲》中“坚持启发式,反对注入式”的教学要求。 根据这一基本原
理,我采用如下教学方法: 提问、观察法、发现法、讲述、启发式相结合的方法。 新课
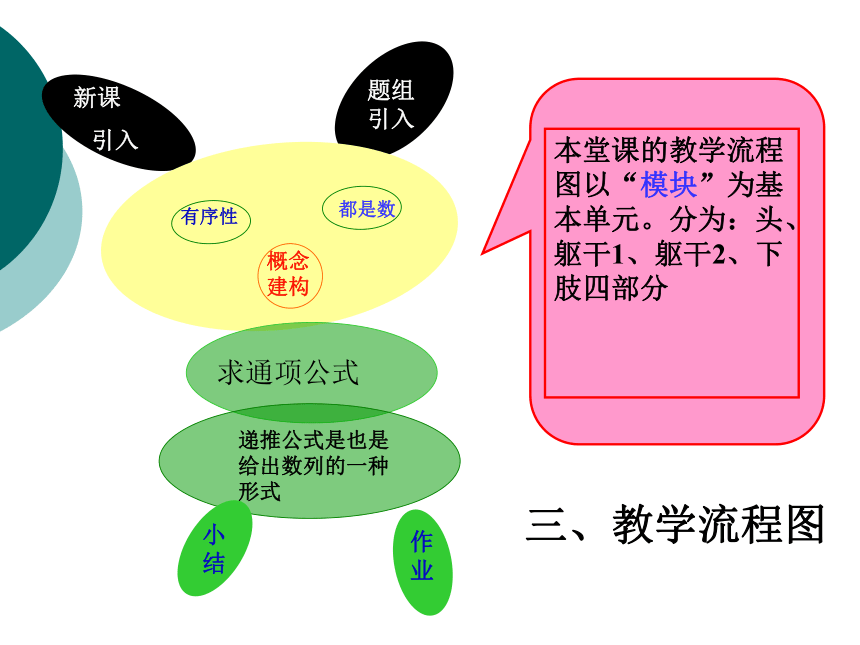
引入题组 引入有序性都是数概念
建构求通项公式递推公式是也是给出数列的一种形式小结作业三、教学流程图设计说明一、板书设计二、时间安排课题引入约5分钟,定义的理解约7分钟,通项公式的探索约5分钟,实践练习约15分钟,根据递推公式求数列的前几项5分钟,小结与作业约3分钟.(注:一节课40分钟) 新课引入 泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝。
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,最底下的一层有100颗宝石,第二层有99颗,第三层98颗,依次类推,最多可放多少层?第57层有多少颗?(见左图)3、数列与数集的主要区别:思考:⑴数列中各项排列有序、数集中各元素排列无序;⑵数列中的项可重复出现、数集中各元素必须互异;
数列与函数的关系:数列的实质:定义域为正整数集(或其有限子集1,2,…n)
的函数当自变量从小到大依次取值时对应的一列函数值;
数列的表示法(回忆函数的表示法)
(3)通项公式法(解析式法):
(2)图象法:
导入:陵寝中第57层有多少颗宝石呢?分析: 序号 n: 1 2 3 4… 57 对应项n结论:…(三)通项公式:100 99 98 97 ? ?(双重身份)例1、根据下面数列的通项公式,写出它的前5项。⑴⑵解:将1,2,3,4,5分别代入各通项公式,可得前5项; 1 2 3 4 511 2 3 4 51-1问题:是否为数列⑴中的项,怎么判别?数列 ⑴ 的图象数列 ⑵ 的图象例2、写出下面数列的一个通项公式,使它的前几项分别是下列各数:⑴ 1,3,5,7 …⑵⑶解:⑴⑵⑶思考:若数列(3)前四项为:通项公式”找起来”就… 课堂练习:观察下面数列的特点, 写出每个数列的一个通项公式:⑴ ⑵ 3,5,3,5,…⑶某班姓赵、钱、孙、李 、王、沈、徐…的人数依次为:
1、 8、 0、 3、 3、 2、 5 …;递推公式的引入:
如前面所举陵寝中三角形图案,我们知道数列的通项公
式是 ,只要依次用n=1,2,3,……100代替公式
中的n,就可以求出数列的各项.
此数列还可以用如下方法给出:第一层是100,从第二层起,每层放的宝石数比前一层少1,即:
100, 99, 98,……3, 2, 1通项公式:
递推公式: 通项公式和递推公式,
是给出一个数列的两种重要方法. 通项公式:递推公式:100, 99, 98,……3, 2, 1学生练习:课本例3(让学生体会递推公式也给出是数列的一种方法)小结: 知识·方法·思想探索是数学的生命线,创新是一个民族的灵魂!作业: (一)书面作业: 1、2、3、4
(二)弹性作业:
前面所举的陵寝三 角图案的数列 有什么特征,如果
改为每层相差2或相差3,你能求出它的通项公式吗?
作业巩固三、教学特色以问题作为教学的主线以学生作为活动的主体谢谢!
数列是高中数学的重要内容之一,它的地位作用可以从三个方面来看:
(1)数列有着广泛的实际应用。如堆放物品总数的计算要用到数列前n项和公式;又如产品规格设计的某些问题要用到等比数列的原理;再如储蓄、分期付款的有关计算也要用到数列的一些知识。
(2)数列起着承前启后的作用。一方面,初中数学的许多内容在解决数列的某些问题中得到了充分运用,数列与前面学习的函数等知识有密切的联系;数列是刻画离散现象的函数,是一种重要的数学模型,人们往往通过离散现象认识连续现象.另一方面,学习数列又为进一步学习数列的极限等内容作好了准备。因此就有必要研究数列。
(3)数列是培养学生数学能力的良好题材。学习数列,要经常观察、分析、归纳、猜想,还要综合运用前面的知识解决数列中的一些问题,这些都有助于学生数学能力的提高。(二)课时安排与说明 教学重难点: 教学重点:数列的概念及数列的通项公式。
教学难点:根据数列的前几项写出数列
的一个通项公式 。
依据:学生的认知水平依据:教材和考试大纲一、知识目标:通过枚举归纳:
?① 认识数列的特点,掌握数列的概念及表示方法。
?②?了解数列通项公式的意义及数列分类。
?③能由数列的通项公式求出数列的各项,反之, 能由数列的前几项写出数列的 一个通项公式。
二、能力目标:通过对数列通项公式的探究和应用,帮助学生通过问题解决获得数学知识;在交流过程中,养成表述、抽象、类比、概括、总结的思维习惯。
三、情感目标:通过各种有趣的,贴近学生生活的素材激发学生的学习兴趣和热爱生活的情感。
二、说教法 根据《教学大纲》中“坚持启发式,反对注入式”的教学要求。 根据这一基本原
理,我采用如下教学方法: 提问、观察法、发现法、讲述、启发式相结合的方法。 新课
引入题组 引入有序性都是数概念
建构求通项公式递推公式是也是给出数列的一种形式小结作业三、教学流程图设计说明一、板书设计二、时间安排课题引入约5分钟,定义的理解约7分钟,通项公式的探索约5分钟,实践练习约15分钟,根据递推公式求数列的前几项5分钟,小结与作业约3分钟.(注:一节课40分钟) 新课引入 泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝。
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,最底下的一层有100颗宝石,第二层有99颗,第三层98颗,依次类推,最多可放多少层?第57层有多少颗?(见左图)3、数列与数集的主要区别:思考:⑴数列中各项排列有序、数集中各元素排列无序;⑵数列中的项可重复出现、数集中各元素必须互异;
数列与函数的关系:数列的实质:定义域为正整数集(或其有限子集1,2,…n)
的函数当自变量从小到大依次取值时对应的一列函数值;
数列的表示法(回忆函数的表示法)
(3)通项公式法(解析式法):
(2)图象法:
导入:陵寝中第57层有多少颗宝石呢?分析: 序号 n: 1 2 3 4… 57 对应项n结论:…(三)通项公式:100 99 98 97 ? ?(双重身份)例1、根据下面数列的通项公式,写出它的前5项。⑴⑵解:将1,2,3,4,5分别代入各通项公式,可得前5项; 1 2 3 4 511 2 3 4 51-1问题:是否为数列⑴中的项,怎么判别?数列 ⑴ 的图象数列 ⑵ 的图象例2、写出下面数列的一个通项公式,使它的前几项分别是下列各数:⑴ 1,3,5,7 …⑵⑶解:⑴⑵⑶思考:若数列(3)前四项为:通项公式”找起来”就… 课堂练习:观察下面数列的特点, 写出每个数列的一个通项公式:⑴ ⑵ 3,5,3,5,…⑶某班姓赵、钱、孙、李 、王、沈、徐…的人数依次为:
1、 8、 0、 3、 3、 2、 5 …;递推公式的引入:
如前面所举陵寝中三角形图案,我们知道数列的通项公
式是 ,只要依次用n=1,2,3,……100代替公式
中的n,就可以求出数列的各项.
此数列还可以用如下方法给出:第一层是100,从第二层起,每层放的宝石数比前一层少1,即:
100, 99, 98,……3, 2, 1通项公式:
递推公式: 通项公式和递推公式,
是给出一个数列的两种重要方法. 通项公式:递推公式:100, 99, 98,……3, 2, 1学生练习:课本例3(让学生体会递推公式也给出是数列的一种方法)小结: 知识·方法·思想探索是数学的生命线,创新是一个民族的灵魂!作业: (一)书面作业: 1、2、3、4
(二)弹性作业:
前面所举的陵寝三 角图案的数列 有什么特征,如果
改为每层相差2或相差3,你能求出它的通项公式吗?
作业巩固三、教学特色以问题作为教学的主线以学生作为活动的主体谢谢!
