22.2 二次函数与一元二次方程课件
文档属性
| 名称 | 22.2 二次函数与一元二次方程课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 100.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-06 00:00:00 | ||
图片预览








文档简介
课件21张PPT。二次函数与一元二次方程 温故知新(1)一次函数y=x+2的图象与x轴的交点为( , )
一元一次方程x+2=0的根为________
(2) 一次函数y=-3x+6的图象与x轴的交点为( , )
一元一次方程-3x+6=0的根为________
思考:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
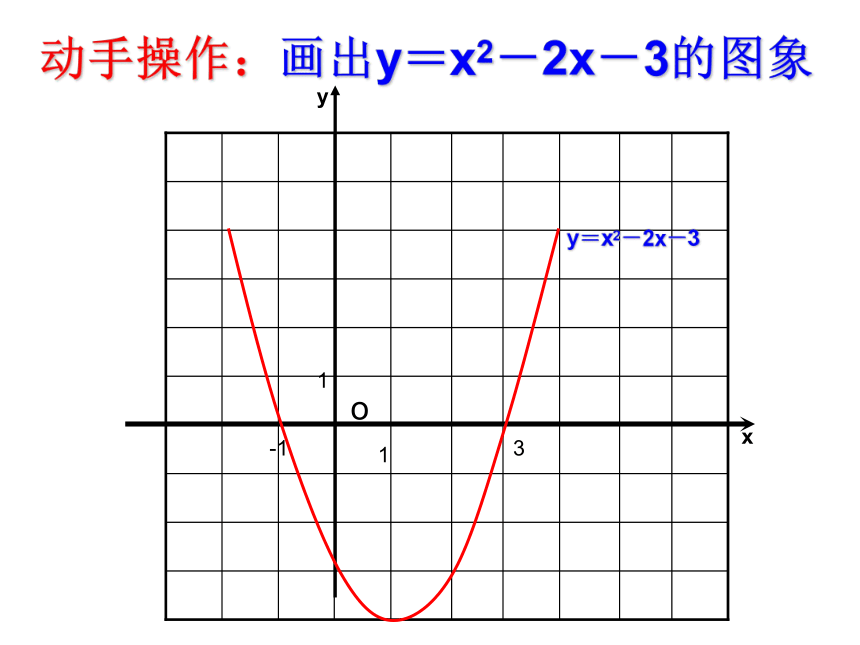
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根 -2 0-22 02动手操作:画出y=x2-2x-3的图象y=x2-2x-3o113-1探究一:你的图象与x轴的交点坐标是什么?函数y=x2-2x-3的图象与x轴两个交点为
(-1,0)(3,0)
方程x2-2x-3 =0的两根是
x1= -1 ,x2 = 3
你发现了什么?
(1)二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是当y=0时一元二次方程ax2+bx+c=0的根
(2)二次函数的图象与x轴交点问题可以转化为一元二次方程去解决例题精讲1. 求抛物线y=x2+4x-5与x轴的交点坐标
解:令y=0
则x2+4x-5 =0
解之得,x1= -5 ,x2 = 1
∴交点坐标为:(-5,0)(1,0)
结论一:
若一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是
A( ), B( )
思考:抛物线y=-x2+6x-9和y=2x2+3x+5与x轴的交点坐标是什么?试试看!
X1,0X2,0探究二:二次函数图象与x轴的交点个数与一元二次方程的解有关系吗?结论二:
函数图象与x轴有两个交点 方程有两个不相等实数根
函数图象与x轴有一个交点 方程有两个相等实数根
函数图象与x轴没有交点 方程没有实数根
方程的根的情况是由什么决定的?
判别式b2-4ac的符号
结论三:
对于二次函数y=ax2+bx+c,判别式又能给我们什么样的结论?
(1)b2-4ac>0 函数图象与x轴有两个交点
(2)b2-4ac=0 函数图象与x轴有一个交点
(3)b2-4ac<0 函数图象与x轴没有交点
例题精讲
2. 判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y=x2-4x+4;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(1)∵ b2-4ac=02 -4×1×( -1)
>0
∴函数图象与x轴有两个交点 例题精讲
2. 判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(2)
∵ b2-4ac=32 -4× (- 2)×( -9) < 0
∴函数图象与x轴没有交点
例题精讲
2. 判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(3)
∵ b2-4ac=42 -4× 1×4 =0
∴函数图象与x轴有一个交点
例题精讲
2. 判断下列二次函数的图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(4)
∵ b2-4ac=(a+b)2 -4× ( -a )×( -b) =( a - b)2 ≥0
∴函数图象与x轴有一个或两个交点
联想:二次函数图象与x轴的交点个数可以借助判别式解决,那么二次函数图象与一次函数图象的交点个数又该怎么解决呢?
例如,抛物线y=x2-2x-3和直线y=x+2有交点吗?有几个?
分析:两个函数图象的交点是这两个函数的公共解,先列出方程组,消去y后,再利用判别式判断即可.例题精讲
3.抛物线y=x2-x-3和直线y=x+b只有一个公共点,求出b的值.
解:由题意,得
消元,得 x2-x-3 =x+b
整理,得x2-2x -(3 + b) =0
∵有唯一交点
∴(-2)2 +4( 3 + b) =0
解之得,b =-4y=x2-x-3y=x+b二、基础训练1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;
3、已知抛物线y=x2+px+q与x轴的两个交点为(-2,0),(3,0),则p= ,q= 。2、已知抛物线y=x2-3x+a+1与x轴最多只有一个交点,则a的范围是 。4、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
(3)y=x2-4x+45、抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0
(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0
(D)a<0 b2-4ac<0
D6、已知抛物线y=x2-(m2+8)x+2(m2+6).
求证:不任m为何实数,抛物线与x轴都有两个不同的交点,三、提高题1、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)如果二次函数y=x2-kx-2+k与轴两个交点为A、B,设此抛物线与y轴的交点为C,当k为6时,求S△ABC .2、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,求m的值。
四、小结1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系。体现了数形结合的思想。
一元一次方程x+2=0的根为________
(2) 一次函数y=-3x+6的图象与x轴的交点为( , )
一元一次方程-3x+6=0的根为________
思考:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根 -2 0-22 02动手操作:画出y=x2-2x-3的图象y=x2-2x-3o113-1探究一:你的图象与x轴的交点坐标是什么?函数y=x2-2x-3的图象与x轴两个交点为
(-1,0)(3,0)
方程x2-2x-3 =0的两根是
x1= -1 ,x2 = 3
你发现了什么?
(1)二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是当y=0时一元二次方程ax2+bx+c=0的根
(2)二次函数的图象与x轴交点问题可以转化为一元二次方程去解决例题精讲1. 求抛物线y=x2+4x-5与x轴的交点坐标
解:令y=0
则x2+4x-5 =0
解之得,x1= -5 ,x2 = 1
∴交点坐标为:(-5,0)(1,0)
结论一:
若一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是
A( ), B( )
思考:抛物线y=-x2+6x-9和y=2x2+3x+5与x轴的交点坐标是什么?试试看!
X1,0X2,0探究二:二次函数图象与x轴的交点个数与一元二次方程的解有关系吗?结论二:
函数图象与x轴有两个交点 方程有两个不相等实数根
函数图象与x轴有一个交点 方程有两个相等实数根
函数图象与x轴没有交点 方程没有实数根
方程的根的情况是由什么决定的?
判别式b2-4ac的符号
结论三:
对于二次函数y=ax2+bx+c,判别式又能给我们什么样的结论?
(1)b2-4ac>0 函数图象与x轴有两个交点
(2)b2-4ac=0 函数图象与x轴有一个交点
(3)b2-4ac<0 函数图象与x轴没有交点
例题精讲
2. 判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y=x2-4x+4;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(1)∵ b2-4ac=02 -4×1×( -1)
>0
∴函数图象与x轴有两个交点 例题精讲
2. 判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(2)
∵ b2-4ac=32 -4× (- 2)×( -9) < 0
∴函数图象与x轴没有交点
例题精讲
2. 判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(3)
∵ b2-4ac=42 -4× 1×4 =0
∴函数图象与x轴有一个交点
例题精讲
2. 判断下列二次函数的图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y= x2-4x+4 ;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
解:(4)
∵ b2-4ac=(a+b)2 -4× ( -a )×( -b) =( a - b)2 ≥0
∴函数图象与x轴有一个或两个交点
联想:二次函数图象与x轴的交点个数可以借助判别式解决,那么二次函数图象与一次函数图象的交点个数又该怎么解决呢?
例如,抛物线y=x2-2x-3和直线y=x+2有交点吗?有几个?
分析:两个函数图象的交点是这两个函数的公共解,先列出方程组,消去y后,再利用判别式判断即可.例题精讲
3.抛物线y=x2-x-3和直线y=x+b只有一个公共点,求出b的值.
解:由题意,得
消元,得 x2-x-3 =x+b
整理,得x2-2x -(3 + b) =0
∵有唯一交点
∴(-2)2 +4( 3 + b) =0
解之得,b =-4y=x2-x-3y=x+b二、基础训练1、已知抛物线y=x2-6x+a的顶点在x轴上,则a= ;若抛物线与x轴有两个交点,则a的范围是 ;
3、已知抛物线y=x2+px+q与x轴的两个交点为(-2,0),(3,0),则p= ,q= 。2、已知抛物线y=x2-3x+a+1与x轴最多只有一个交点,则a的范围是 。4、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。
(1)y=6x2-2x+1 (2)y=-15x2+14x+8
(3)y=x2-4x+45、抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0
(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0
(D)a<0 b2-4ac<0
D6、已知抛物线y=x2-(m2+8)x+2(m2+6).
求证:不任m为何实数,抛物线与x轴都有两个不同的交点,三、提高题1、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时,这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)如果二次函数y=x2-kx-2+k与轴两个交点为A、B,设此抛物线与y轴的交点为C,当k为6时,求S△ABC .2、已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值。
(2)若抛物线与直线y=x+2m只有一个交点,求m的值。
四、小结1、若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0 ), B( x2,0 )
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系。体现了数形结合的思想。
同课章节目录
