四年级下册数学人教版5.7 探索多边形的内角和课件(共24张PPT)
文档属性
| 名称 | 四年级下册数学人教版5.7 探索多边形的内角和课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:20:08 | ||
图片预览





文档简介
(共24张PPT)
第五单元 三角形
探索多边形的内角和
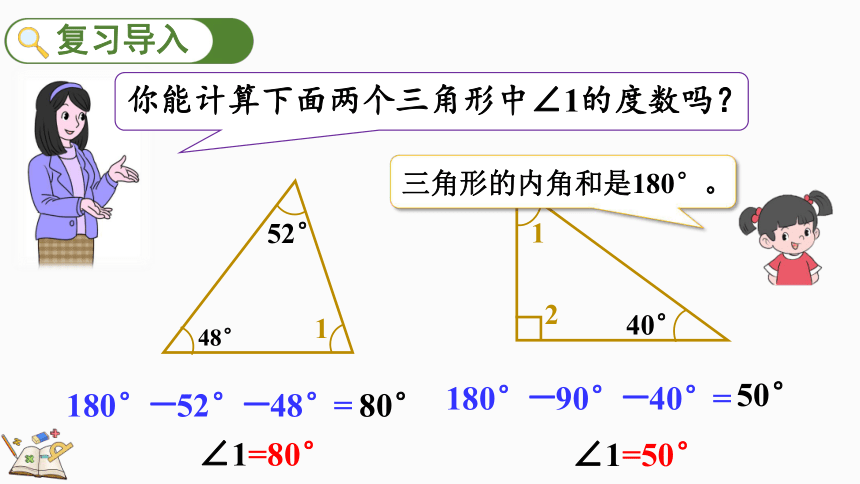
你能计算下面两个三角形中∠1的度数吗?
1
2
40°
52°
48°
1
180°-52°-48°=
80°
180°-90°-40°=
50°
∠1=80°
∠1=50°
三角形的内角和是180°。
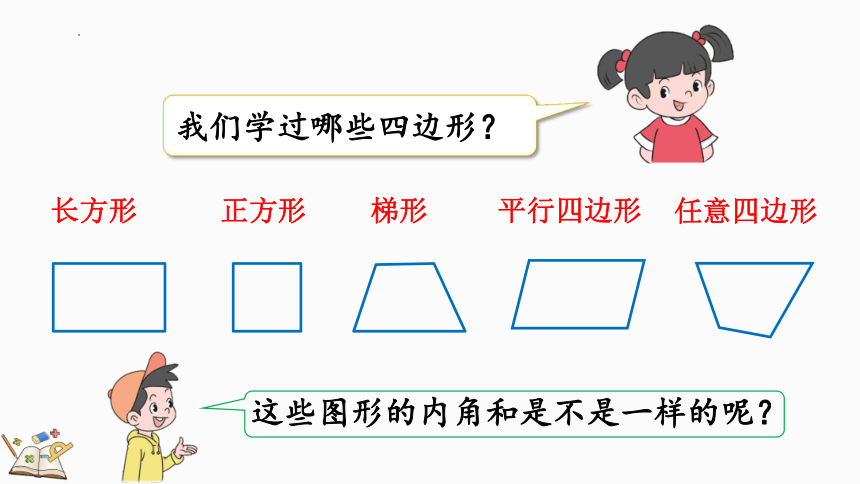
我们学过哪些四边形?
这些图形的内角和是不是一样的呢?
长方形
正方形
梯形
平行四边形
任意四边形
四边形的内角和是多少度?
7
我们学过哪些四边形?
长方形
正方形
梯形
平行四边形
任意四边形
这些图形的内角和是不是一样的呢?
阅读与理解
小组讨论
正方形和长方形的角有什么特征?
1.
和小组同学说一说你的看法。
2.
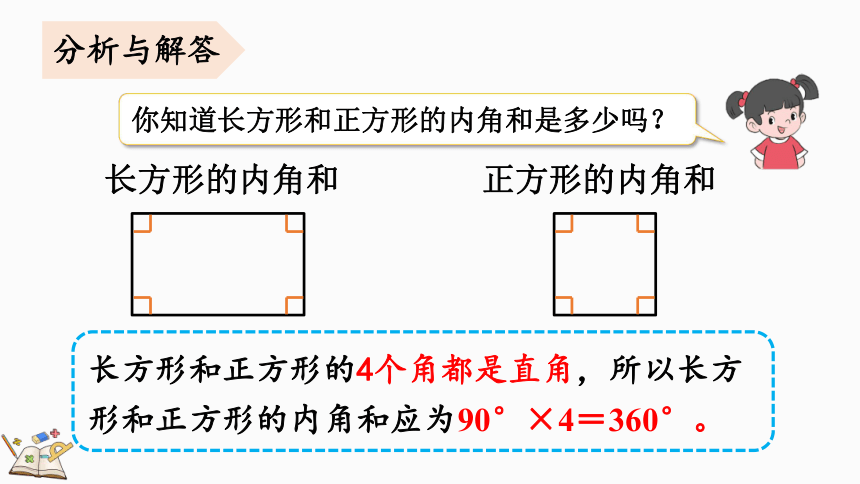
长方形的内角和
正方形的内角和
长方形和正方形的4个角都是直角,所以长方形和正方形的内角和应为90°×4=360°。
你知道长方形和正方形的内角和是多少吗?
分析与解答
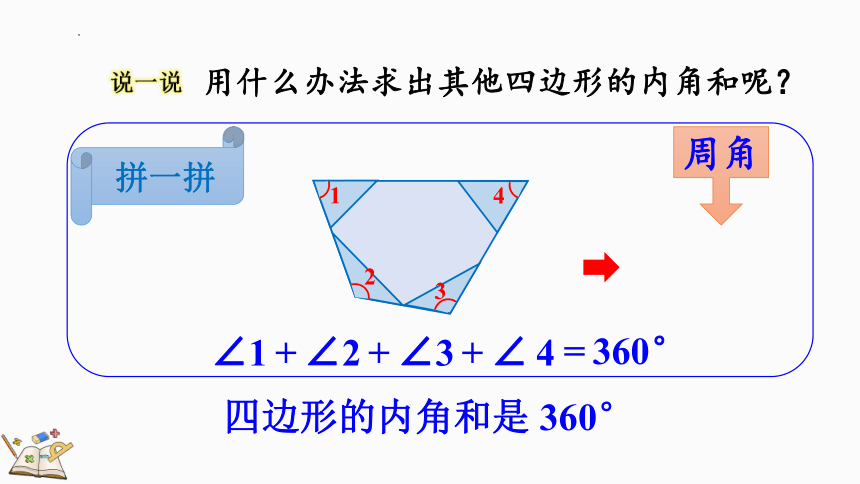
用什么办法求出其他四边形的内角和呢?
我把这个四边形的4个角剪下来,拼成一个周角。
我把这个四边形分成了2个三角形。
说一说
3
1
2
4
周角
1
2
4
3
四边形的内角和是 360°
拼一拼
∠1+∠2+∠3+∠4
=360°
用什么办法求出其他四边形的内角和呢?
说一说
小组讨论
你还能想出其他方法吗?结合三角形内角和的知识想一想。
1.
和小组同学说一说你的方法,你发现了什么?
2.
分一分:
由图可知:
∠A+∠B+∠C+∠D
=(∠1+∠2)+∠B+(∠3+∠4)+∠D
=(∠1+∠3+∠D)+(∠2+∠4+∠B)
=180°+180°=360°
A
B
D
C
1
2
3
4
如何计算呢?
分析与解答
180°+180°=360°
四边形的内角和是360°。
四边形都可以分成两个三角形。
分析与解答
我们大家共同发现了所有四边形的内角和都是360°。
答:四边形的内角和是360°。
四边形的内角和是多少度?
7
长方形
正方形
梯形
平行四边形
任意四边形
你能想办法求出下边这个多边形的内角和吗
180°×4 = 720°
我把这个六边形分成了4个三角形。
多边形的内角和 = 180°×(边数-2)
选自教材第66页做一做
1
你能想办法求出下边这个多边形的内角和吗
180°×6-360°=720°
我把这个六边形分成了6个三角形,把6个三角形的内角加起来再减去中间的一个周角就是六边形的内角和。
多边形的内角和 = 180°×边数- 360°
1
选自教材第66页做一做
多边形的内角和=180°×边数-360°
多边形的内角和=180°×(边数-2)
180°×(边数-2)= 180°×边数-360°
选自教材第66页做一做
如果用四则运算的法则,去括号,第一个算式就变成了第二个算式。用不同的分法得出的结论是相同的。
你能想办法求出下边这个多边形的内角和吗
6
7
2
3
180°×5
180°×4
多边形的内角和=180°×(边数-2)
1
选自教材第66页做一做
你能想办法求出下边这个多边形的内角和吗
6
7
多边形的内角和=180°×边数-360°
1
360°
540°
720°
900°
选自教材第66页做一做
剩下的图形是三角形
将下面的四边形剪去一个角,剩下图形的
内角和可能是多少度?
剪法一:
内角和是180°
1
答:剩下图形的内角和可能是180°、540°或360°。
剪法二:
剪法三:
剩下的图形是五边形
内角和是(5-2)×180°=540°
剩下的图形是四边形
内角和是360°
1
70°
75°
60°
?
120°
130°
93°
?
计算下图中未知角的度数。
(1)
(2)
2
360° 90° 75° 60°
答:四边形中未知角的度数是135°。
根据四边形的内角和是360°列式计算。
75°
60°
?
(1)
=135°
2
540° 70° 120° 130° 93°
70°
?
120°
130°
93°
根据(5-2)×180°=540°可知五边形的内角和540° 。
=127°
答:五边形中未知角的度数是127°。
2
这节课有什么收获呢?
2.多边形的内角和是180°×(边数-2)。
1.四边形的内角和是360°。
多边形的内角和
探索多边形的内角和
四边形的内角和是360°。
A
B
D
C
多边形的内角和是
180°×(边数-2) 。
第五单元 三角形
探索多边形的内角和
你能计算下面两个三角形中∠1的度数吗?
1
2
40°
52°
48°
1
180°-52°-48°=
80°
180°-90°-40°=
50°
∠1=80°
∠1=50°
三角形的内角和是180°。
我们学过哪些四边形?
这些图形的内角和是不是一样的呢?
长方形
正方形
梯形
平行四边形
任意四边形
四边形的内角和是多少度?
7
我们学过哪些四边形?
长方形
正方形
梯形
平行四边形
任意四边形
这些图形的内角和是不是一样的呢?
阅读与理解
小组讨论
正方形和长方形的角有什么特征?
1.
和小组同学说一说你的看法。
2.
长方形的内角和
正方形的内角和
长方形和正方形的4个角都是直角,所以长方形和正方形的内角和应为90°×4=360°。
你知道长方形和正方形的内角和是多少吗?
分析与解答
用什么办法求出其他四边形的内角和呢?
我把这个四边形的4个角剪下来,拼成一个周角。
我把这个四边形分成了2个三角形。
说一说
3
1
2
4
周角
1
2
4
3
四边形的内角和是 360°
拼一拼
∠1+∠2+∠3+∠4
=360°
用什么办法求出其他四边形的内角和呢?
说一说
小组讨论
你还能想出其他方法吗?结合三角形内角和的知识想一想。
1.
和小组同学说一说你的方法,你发现了什么?
2.
分一分:
由图可知:
∠A+∠B+∠C+∠D
=(∠1+∠2)+∠B+(∠3+∠4)+∠D
=(∠1+∠3+∠D)+(∠2+∠4+∠B)
=180°+180°=360°
A
B
D
C
1
2
3
4
如何计算呢?
分析与解答
180°+180°=360°
四边形的内角和是360°。
四边形都可以分成两个三角形。
分析与解答
我们大家共同发现了所有四边形的内角和都是360°。
答:四边形的内角和是360°。
四边形的内角和是多少度?
7
长方形
正方形
梯形
平行四边形
任意四边形
你能想办法求出下边这个多边形的内角和吗
180°×4 = 720°
我把这个六边形分成了4个三角形。
多边形的内角和 = 180°×(边数-2)
选自教材第66页做一做
1
你能想办法求出下边这个多边形的内角和吗
180°×6-360°=720°
我把这个六边形分成了6个三角形,把6个三角形的内角加起来再减去中间的一个周角就是六边形的内角和。
多边形的内角和 = 180°×边数- 360°
1
选自教材第66页做一做
多边形的内角和=180°×边数-360°
多边形的内角和=180°×(边数-2)
180°×(边数-2)= 180°×边数-360°
选自教材第66页做一做
如果用四则运算的法则,去括号,第一个算式就变成了第二个算式。用不同的分法得出的结论是相同的。
你能想办法求出下边这个多边形的内角和吗
6
7
2
3
180°×5
180°×4
多边形的内角和=180°×(边数-2)
1
选自教材第66页做一做
你能想办法求出下边这个多边形的内角和吗
6
7
多边形的内角和=180°×边数-360°
1
360°
540°
720°
900°
选自教材第66页做一做
剩下的图形是三角形
将下面的四边形剪去一个角,剩下图形的
内角和可能是多少度?
剪法一:
内角和是180°
1
答:剩下图形的内角和可能是180°、540°或360°。
剪法二:
剪法三:
剩下的图形是五边形
内角和是(5-2)×180°=540°
剩下的图形是四边形
内角和是360°
1
70°
75°
60°
?
120°
130°
93°
?
计算下图中未知角的度数。
(1)
(2)
2
360° 90° 75° 60°
答:四边形中未知角的度数是135°。
根据四边形的内角和是360°列式计算。
75°
60°
?
(1)
=135°
2
540° 70° 120° 130° 93°
70°
?
120°
130°
93°
根据(5-2)×180°=540°可知五边形的内角和540° 。
=127°
答:五边形中未知角的度数是127°。
2
这节课有什么收获呢?
2.多边形的内角和是180°×(边数-2)。
1.四边形的内角和是360°。
多边形的内角和
探索多边形的内角和
四边形的内角和是360°。
A
B
D
C
多边形的内角和是
180°×(边数-2) 。
