四年级下册数学人教版5.8 三角形练习十六课件(共30张PPT)
文档属性
| 名称 | 四年级下册数学人教版5.8 三角形练习十六课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:20:15 | ||
图片预览



文档简介
(共30张PPT)
第五单元 三角形
练习十六
三角形的内角和
探索多边形的内角和
上两节课我们都学习了哪些知识?
三角形的内角和
1
2
3
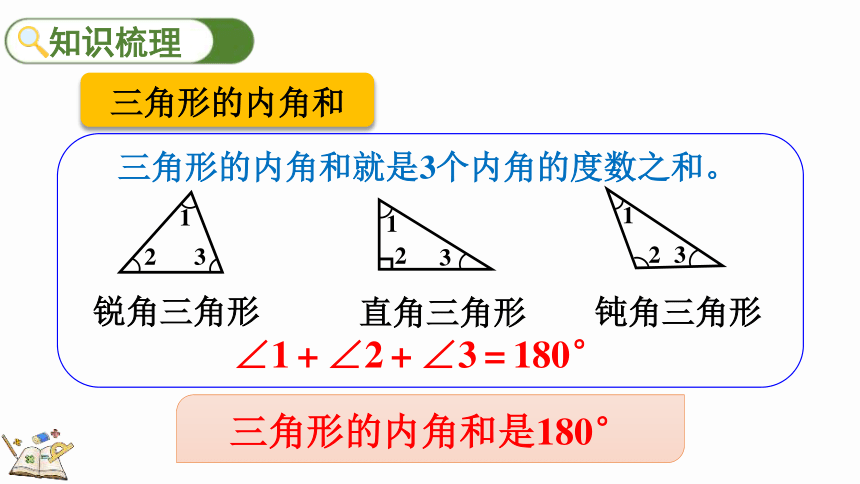
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
∠1+∠2+∠3=180°
三角形的内角和就是3个内角的度数之和。
三角形的内角和是180°
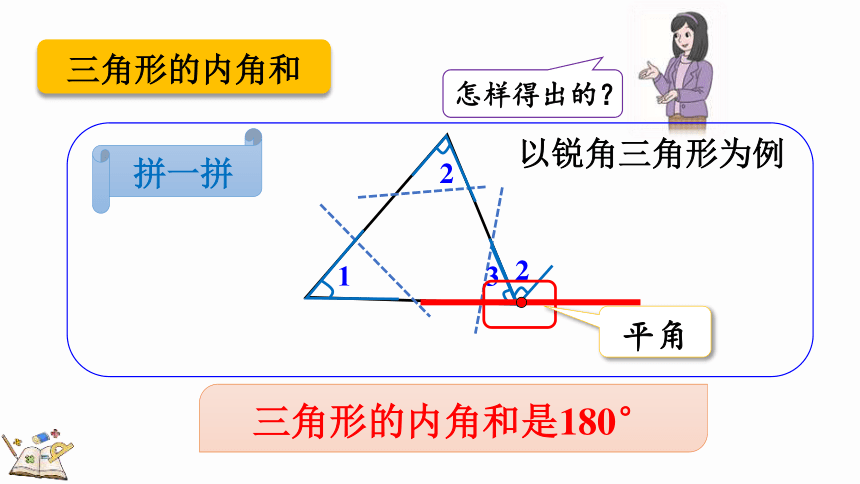
怎样得出的?
2
1
3
2
以锐角三角形为例
三角形的内角和
三角形的内角和是180°
平角
拼一拼
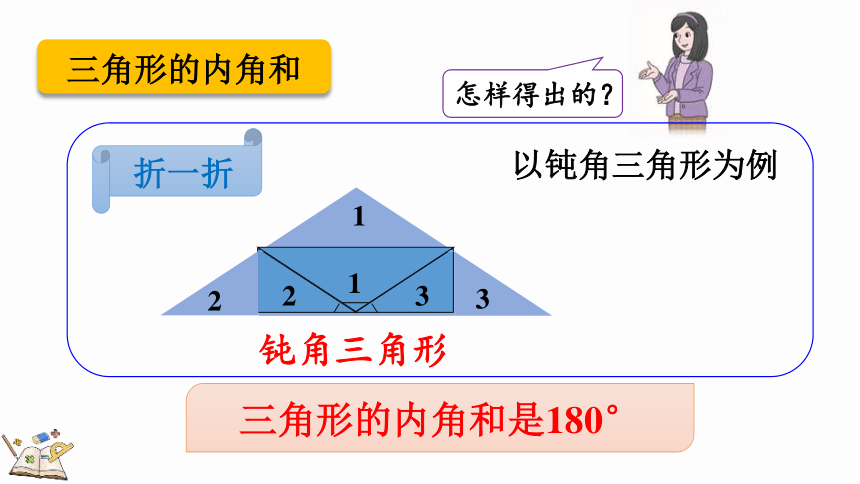
怎样得出的?
三角形的内角和
三角形的内角和是180°
折一折
3
2
1
1
2
3
钝角三角形
以钝角三角形为例
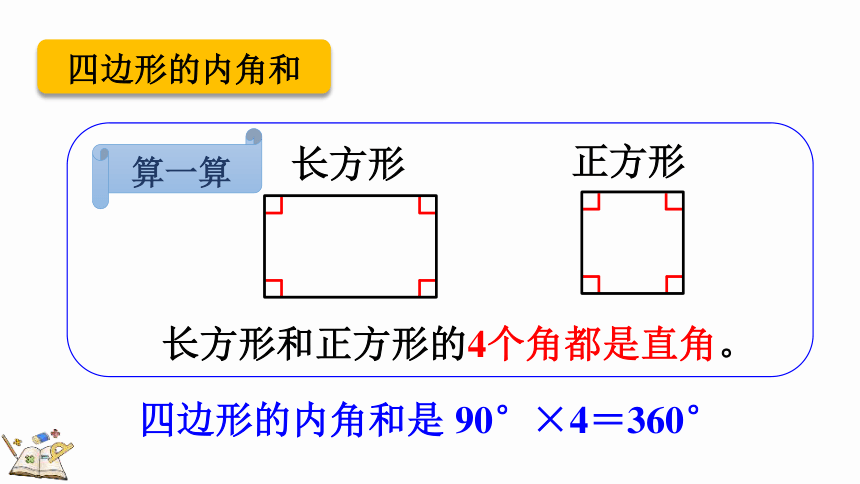
四边形的内角和
四边形的内角和是 90°×4=360°
长方形
正方形
长方形和正方形的4个角都是直角。
算一算
怎样得出的?
3
1
2
4
1
2
4
3
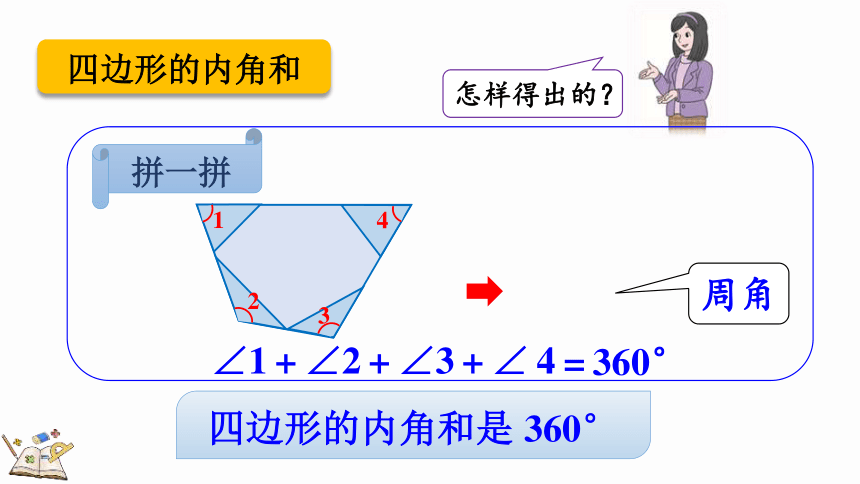
四边形的内角和
四边形的内角和是 360°
∠1+∠2+∠3+∠4
=360°
拼一拼
周角
怎样得出的?
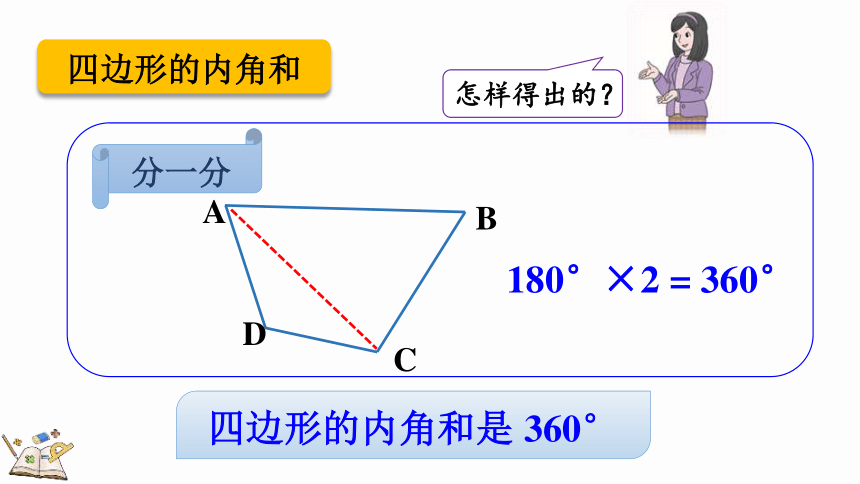
四边形的内角和
A
B
D
C
180°×2 = 360°
四边形的内角和是 360°
分一分
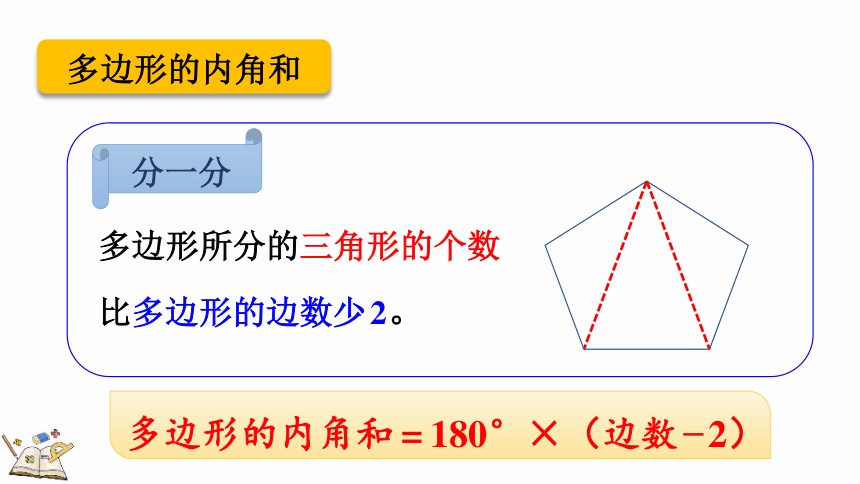
多边形的内角和
多边形所分的三角形的个数比多边形的边数少2。
多边形的内角和=180°×(边数 2)
分一分
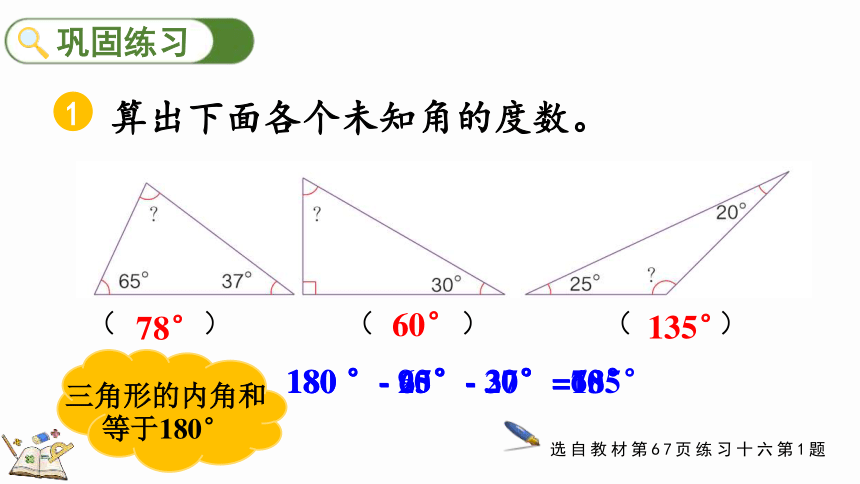
算出下面各个未知角的度数。
选自教材第67页练习十六第1题
1
( ) ( ) ( )
78°
60°
135°
180 °- 65°- 37°=78°
180 °- 90°- 30°=60°
180 °- 25°- 20°=135°
三角形的内角和等于180°
选自教材第67页练习十六第2题
2
求出下列三角形各个角的度数。
(1)一个等边三角形。
(2)一个等腰三角形,顶角是96°。
(3)一个直角三角形,其中一个锐角是40°。
选自教材第67页练习十六第2题
2
求出下列三角形各个角的度数。
(1)一个等边三角形。
180°÷3=60°
三个角都为60°。
等边三角形的三个角相等。
选自教材第67页练习十六第2题
2
求出下列三角形各个角的度数。
(2)一个等腰三角形,顶角是96°。
(180° 96°)÷2=42°
底角是42°。
等腰三角形的两个底角相等。
选自教材第67页练习十六第2题
2
求出下列三角形各个角的度数。
(3)一个直角三角形,其中一个锐角是40°。
90° 40°=50°
另一个锐角是50°。
两个锐角的和是90°。
答:风筝的顶角是40°。
180° 70° 70°
= 40°
3
爸爸给小红买了一个等腰三角形 的风筝。风筝的一个底角是70°,
风筝的顶角是多少度?
等腰三角形的两个底角大小相等。
选自教材第67页练习十六第3题
4
选自教材第67页练习十五第4题
画一画,算一算,你发现了什么?
图形
边数
内角和
3
4
5
180°
180°×( )
180°×( )
……
……
……
6
7
2
180°×4
180°×5
多边形的内角和=180°×(边数 2)
发现:
3
5
选自教材第68页练习十五第5题
连一连。
有一个直角,有两条相等。
只有两个锐角,没有直角。
三个角相等。
没有直角和钝角。
锐角三角形
直角三角形
钝角三角形
等腰三角形
等边三角形
6
选自教材第68页练习十六第6题
猜一猜。
(1)
(2)
在三角形中,一个角是直角,另外两个角可能各是多少度?
三角形的两条边分别是3 cm和4 cm,另一条边可能是多少厘米(取整厘米数)?
6
选自教材第68页练习十六第6题
猜一猜。
(1)
在三角形中,一个角是直角,另外两个角可能各是多少度?
另两个角的和为90°即可,如30°和60°
(答案不唯一)
180°-90°=90°
6
选自教材第68页练习十六第6题
猜一猜。
(2)
三角形的两条边分别是3 cm和4 cm,另一条边可能是多少厘米(取整厘米数)?
另一条边的长必须 大于1cm,小于7cm。如2 cm、3 cm。
3+4=7(cm)
4-3=1(cm)
(答案不唯一)
选自教材第68页练习十六第7题
1个
3个
6个
10个
(1)
(1+2)
(1+2+3)
(1+2+3+4)
每次增加的三角形个数等于每幅图中基本三角形的个数。
下面图形中各有多少个三角形?有什么规律?
7
选自教材第68页练习十六第7题
1个
3个
6个
10个
(1)
(1+2)
(1+2+3)
(1+2+3+4)
答:图形中分别有1个,3个,6个,10个三角形。
下面图形中各有多少个三角形?有什么规律?
7
选自教材第68页练习十六第7题
1个
3个
6个
10个
从三角形的一个顶点向对边引若干条线段,若图形里有n个基本三角形,则这个图形里一共有 [n+(n-1) +… +2+1]个三角形。
下面图形中各有多少个三角形?有什么规律?
7
8
一个等腰三角形,它的一个底角是50°,它的顶角
是多少度
180°-50°×2
= 180°-100°
= 80°
答:它的顶角是80°。
等腰三角形的两个底角相等。
9
一个直角三角形,其中一个锐角是36°,另一个
锐角是多少度
180°-90°-36°
= 90°-36°
= 54°
答:另一个锐角是54°。
50°
70°
1
2
∠1=50°+70°
50°+70°+∠2=180°
答:∠1是120 °。
根据三角形的内角和以及平角的定义进行求解。
如下图,∠1是多少度
10
∠1+∠2=180°
50°+70°+∠2=∠1+∠2
∠1=120°
三角形ABC的周长是84 cm,且∠B = ∠C,
BC = 24 cm,求AB的长。
A
B
C
∠B=∠C
ABC为等腰三角形
AB=AC
(84 24)÷2
= 60 ÷2
= 30(cm)
答:AB的长为30 cm。
1
在一个三角形中,最大角的度数是最小角的
3倍,另一个角的度数是最小角的2倍,求这
个三角形的三个角的度数。
2
将此三角形的最小角看作一份,则3个内角的和就是这样的(1+2+3)= 6份,由此即可求出最小角的度数。
180°÷ 6 = 30°
30°× 2 = 60°
30°× 3 = 90°
答:这个三角形的三个角的度数分别为
30°、60°、90°。
这节课有什么收获呢?
内角和
三角形内角和是180°
四边形内角和是360°
多边形内角和是180°×(n-2)
内角和
三角形内角和是180°。
四边形内角和是360°。
多边形内角和是
180°×(边数 2)
练习十六
第五单元 三角形
练习十六
三角形的内角和
探索多边形的内角和
上两节课我们都学习了哪些知识?
三角形的内角和
1
2
3
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
∠1+∠2+∠3=180°
三角形的内角和就是3个内角的度数之和。
三角形的内角和是180°
怎样得出的?
2
1
3
2
以锐角三角形为例
三角形的内角和
三角形的内角和是180°
平角
拼一拼
怎样得出的?
三角形的内角和
三角形的内角和是180°
折一折
3
2
1
1
2
3
钝角三角形
以钝角三角形为例
四边形的内角和
四边形的内角和是 90°×4=360°
长方形
正方形
长方形和正方形的4个角都是直角。
算一算
怎样得出的?
3
1
2
4
1
2
4
3
四边形的内角和
四边形的内角和是 360°
∠1+∠2+∠3+∠4
=360°
拼一拼
周角
怎样得出的?
四边形的内角和
A
B
D
C
180°×2 = 360°
四边形的内角和是 360°
分一分
多边形的内角和
多边形所分的三角形的个数比多边形的边数少2。
多边形的内角和=180°×(边数 2)
分一分
算出下面各个未知角的度数。
选自教材第67页练习十六第1题
1
( ) ( ) ( )
78°
60°
135°
180 °- 65°- 37°=78°
180 °- 90°- 30°=60°
180 °- 25°- 20°=135°
三角形的内角和等于180°
选自教材第67页练习十六第2题
2
求出下列三角形各个角的度数。
(1)一个等边三角形。
(2)一个等腰三角形,顶角是96°。
(3)一个直角三角形,其中一个锐角是40°。
选自教材第67页练习十六第2题
2
求出下列三角形各个角的度数。
(1)一个等边三角形。
180°÷3=60°
三个角都为60°。
等边三角形的三个角相等。
选自教材第67页练习十六第2题
2
求出下列三角形各个角的度数。
(2)一个等腰三角形,顶角是96°。
(180° 96°)÷2=42°
底角是42°。
等腰三角形的两个底角相等。
选自教材第67页练习十六第2题
2
求出下列三角形各个角的度数。
(3)一个直角三角形,其中一个锐角是40°。
90° 40°=50°
另一个锐角是50°。
两个锐角的和是90°。
答:风筝的顶角是40°。
180° 70° 70°
= 40°
3
爸爸给小红买了一个等腰三角形 的风筝。风筝的一个底角是70°,
风筝的顶角是多少度?
等腰三角形的两个底角大小相等。
选自教材第67页练习十六第3题
4
选自教材第67页练习十五第4题
画一画,算一算,你发现了什么?
图形
边数
内角和
3
4
5
180°
180°×( )
180°×( )
……
……
……
6
7
2
180°×4
180°×5
多边形的内角和=180°×(边数 2)
发现:
3
5
选自教材第68页练习十五第5题
连一连。
有一个直角,有两条相等。
只有两个锐角,没有直角。
三个角相等。
没有直角和钝角。
锐角三角形
直角三角形
钝角三角形
等腰三角形
等边三角形
6
选自教材第68页练习十六第6题
猜一猜。
(1)
(2)
在三角形中,一个角是直角,另外两个角可能各是多少度?
三角形的两条边分别是3 cm和4 cm,另一条边可能是多少厘米(取整厘米数)?
6
选自教材第68页练习十六第6题
猜一猜。
(1)
在三角形中,一个角是直角,另外两个角可能各是多少度?
另两个角的和为90°即可,如30°和60°
(答案不唯一)
180°-90°=90°
6
选自教材第68页练习十六第6题
猜一猜。
(2)
三角形的两条边分别是3 cm和4 cm,另一条边可能是多少厘米(取整厘米数)?
另一条边的长必须 大于1cm,小于7cm。如2 cm、3 cm。
3+4=7(cm)
4-3=1(cm)
(答案不唯一)
选自教材第68页练习十六第7题
1个
3个
6个
10个
(1)
(1+2)
(1+2+3)
(1+2+3+4)
每次增加的三角形个数等于每幅图中基本三角形的个数。
下面图形中各有多少个三角形?有什么规律?
7
选自教材第68页练习十六第7题
1个
3个
6个
10个
(1)
(1+2)
(1+2+3)
(1+2+3+4)
答:图形中分别有1个,3个,6个,10个三角形。
下面图形中各有多少个三角形?有什么规律?
7
选自教材第68页练习十六第7题
1个
3个
6个
10个
从三角形的一个顶点向对边引若干条线段,若图形里有n个基本三角形,则这个图形里一共有 [n+(n-1) +… +2+1]个三角形。
下面图形中各有多少个三角形?有什么规律?
7
8
一个等腰三角形,它的一个底角是50°,它的顶角
是多少度
180°-50°×2
= 180°-100°
= 80°
答:它的顶角是80°。
等腰三角形的两个底角相等。
9
一个直角三角形,其中一个锐角是36°,另一个
锐角是多少度
180°-90°-36°
= 90°-36°
= 54°
答:另一个锐角是54°。
50°
70°
1
2
∠1=50°+70°
50°+70°+∠2=180°
答:∠1是120 °。
根据三角形的内角和以及平角的定义进行求解。
如下图,∠1是多少度
10
∠1+∠2=180°
50°+70°+∠2=∠1+∠2
∠1=120°
三角形ABC的周长是84 cm,且∠B = ∠C,
BC = 24 cm,求AB的长。
A
B
C
∠B=∠C
ABC为等腰三角形
AB=AC
(84 24)÷2
= 60 ÷2
= 30(cm)
答:AB的长为30 cm。
1
在一个三角形中,最大角的度数是最小角的
3倍,另一个角的度数是最小角的2倍,求这
个三角形的三个角的度数。
2
将此三角形的最小角看作一份,则3个内角的和就是这样的(1+2+3)= 6份,由此即可求出最小角的度数。
180°÷ 6 = 30°
30°× 2 = 60°
30°× 3 = 90°
答:这个三角形的三个角的度数分别为
30°、60°、90°。
这节课有什么收获呢?
内角和
三角形内角和是180°
四边形内角和是360°
多边形内角和是180°×(n-2)
内角和
三角形内角和是180°。
四边形内角和是360°。
多边形内角和是
180°×(边数 2)
练习十六
