四年级数学下册人教版7.4 运用平移知识解决面积问题课件(共25张PPT)
文档属性
| 名称 | 四年级数学下册人教版7.4 运用平移知识解决面积问题课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:30:37 | ||
图片预览



文档简介
(共25张PPT)
第七单元 图形的运动(二)
运用平移知识解决
面积问题
物体的形状、大小、方向不变;只有物体的位置发生改变。
平移有什么特点?
怎么画平移图形呢?
在原图形上选择几个能决定图形形状和大小的点。
按要求把选择的点向规定的方向平移规定的格数。
顺次连接各对应点。
1 cm
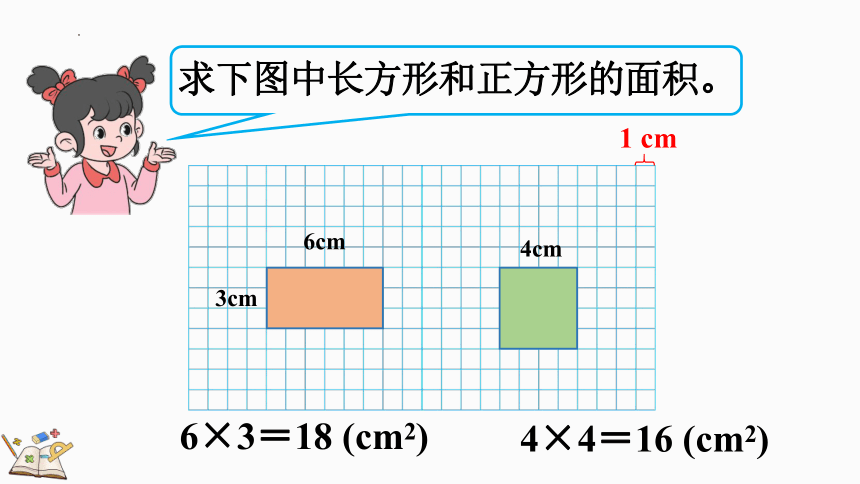
6×3=18 (cm2)
4×4=16 (cm2)
求下图中长方形和正方形的面积。
6cm
3cm
4cm
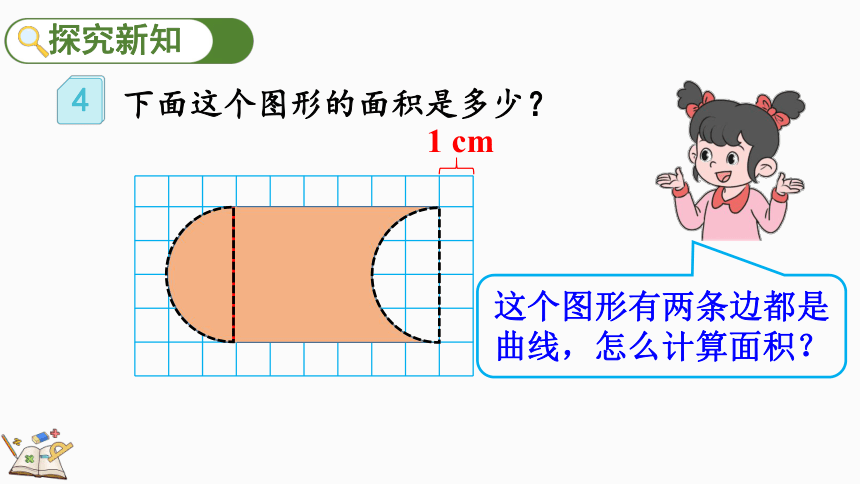
下面这个图形的面积是多少?
4
1 cm
这个图形有两条边都是曲线,怎么计算面积?
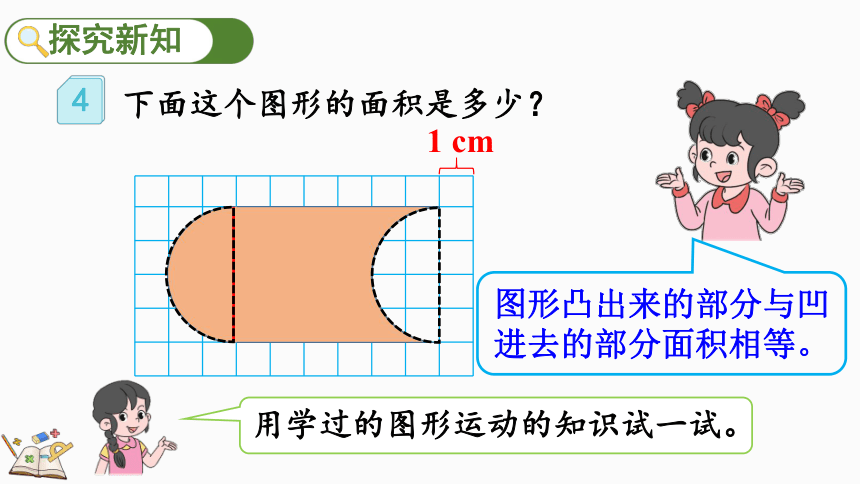
下面这个图形的面积是多少?
4
1 cm
图形凸出来的部分与凹进去的部分面积相等。
用学过的图形运动的知识试一试。
1.你是怎样把图形变为规则图形的?
2.在小组内说一说。
小组讨论
1 cm
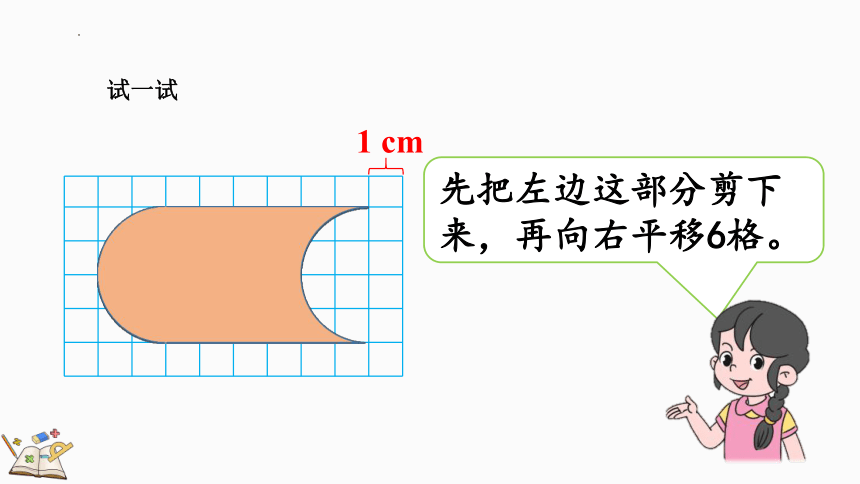
先把左边这部分剪下来,再向右平移6格。
试一试
6格
1 cm
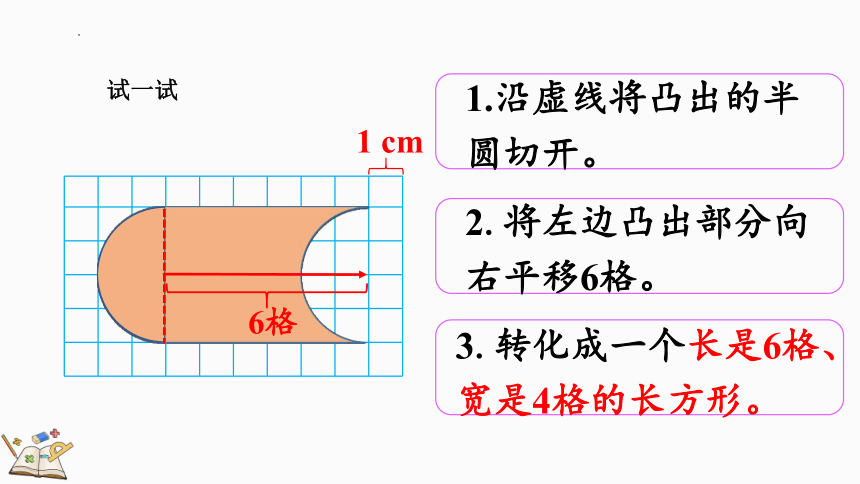
1.沿虚线将凸出的半圆切开。
2.将左边凸出部分向右平移6格。
3.转化成一个长是6格、宽是4格的长方形。
试一试
1 cm
变成了一个长方形,它的面积我会算啦!
6×4=24(cm )
1 cm
答:这个图形的面积是24 cm 。
转化后的长方形与原图形形状不同,但是面积相等,求长方形的面积就相当于是求原图形的面积。
平移
不规则图形
规则图形
割补
面积不变
转化思想
求一些不规则图形的周长或面积时,可以利用割补、平移等方法,将不规则图形转化成规则图形,再根据公式计算。
9×3=27(cm )
答:这个“火箭” 的面积是27 cm 。
画一画,量一量,算出下面这个“火箭”的面积。
9 cm
3 cm
将右边的三角形平移到左边,原图就变成了一个长方形 。
1
选自教材第84页做一做
( )
( )
涂色部分占整个图形的几分之几?
1
3
( )
( )
1
2
( )
( )
3
1
2
选自教材第85页练习二十一第3题
想一想,怎样才能算出下面图形的周长。
1 cm
通过平移不规则图形的边,把它转化成规则的长方形。
10 cm
5 cm
(10+5)×2
= 15×2
= 30(cm)
答:这个图形的周长是30 cm。
3
选自教材第85页练习二十一第4题
1
选择题。
利用转化的思想,通过平移把不规则的图形
转化为规则图形时,图形的面积( )。
A.扩大2倍 B.缩小2倍
C.不变 D.无法确定
C
2
判断题。
计算图形的周长时,不能运用割补或平移的方法把不规则的图形周长转化为规则图形的周长。( )
×
求这个图形的周长和面积(每个小正方形的边长是1cm)。
(5+4)×2=18(cm)
答:这个图形的周长是18cm。
3
求这个图形的周长和面积(每个小正方形的边长是1cm)。
(5+2)×2=14(cm )
答:这个图形的面积是14cm 。
3
5
( )
( )
8
2
6
2
( )
( )
3
1
( )
( )
4
1
涂色部分占整个图形的几分之几?
如图所示,在一块长26 m,宽16 m的长方形
花坛里修了一条宽2 m的曲曲折折的观赏小
路。求花坛的实际面积。
①
②
16-2
26-2
(26-2) ×(16-2)
答:花坛的实际面积是336 m 。
=24×14
=336(m )
将②先向上平移2 m,再向左平移2 m,就可以拼成一个长方形。
这节课有什么收获呢?
求一些不规则图形的周长或面积时,可以利用割补、平移等方法,将不规则图形转化成规则图形,再根据公式计算。
这节课有什么收获呢?
转化图形时,可以将部分图形进行平移,也可以对部分边进行平移。
转化后图形的周长或面积不变。
运用平移知识解决面积问题
平移
不规则图形
规则图形
转化
面积不变
第七单元 图形的运动(二)
运用平移知识解决
面积问题
物体的形状、大小、方向不变;只有物体的位置发生改变。
平移有什么特点?
怎么画平移图形呢?
在原图形上选择几个能决定图形形状和大小的点。
按要求把选择的点向规定的方向平移规定的格数。
顺次连接各对应点。
1 cm
6×3=18 (cm2)
4×4=16 (cm2)
求下图中长方形和正方形的面积。
6cm
3cm
4cm
下面这个图形的面积是多少?
4
1 cm
这个图形有两条边都是曲线,怎么计算面积?
下面这个图形的面积是多少?
4
1 cm
图形凸出来的部分与凹进去的部分面积相等。
用学过的图形运动的知识试一试。
1.你是怎样把图形变为规则图形的?
2.在小组内说一说。
小组讨论
1 cm
先把左边这部分剪下来,再向右平移6格。
试一试
6格
1 cm
1.沿虚线将凸出的半圆切开。
2.将左边凸出部分向右平移6格。
3.转化成一个长是6格、宽是4格的长方形。
试一试
1 cm
变成了一个长方形,它的面积我会算啦!
6×4=24(cm )
1 cm
答:这个图形的面积是24 cm 。
转化后的长方形与原图形形状不同,但是面积相等,求长方形的面积就相当于是求原图形的面积。
平移
不规则图形
规则图形
割补
面积不变
转化思想
求一些不规则图形的周长或面积时,可以利用割补、平移等方法,将不规则图形转化成规则图形,再根据公式计算。
9×3=27(cm )
答:这个“火箭” 的面积是27 cm 。
画一画,量一量,算出下面这个“火箭”的面积。
9 cm
3 cm
将右边的三角形平移到左边,原图就变成了一个长方形 。
1
选自教材第84页做一做
( )
( )
涂色部分占整个图形的几分之几?
1
3
( )
( )
1
2
( )
( )
3
1
2
选自教材第85页练习二十一第3题
想一想,怎样才能算出下面图形的周长。
1 cm
通过平移不规则图形的边,把它转化成规则的长方形。
10 cm
5 cm
(10+5)×2
= 15×2
= 30(cm)
答:这个图形的周长是30 cm。
3
选自教材第85页练习二十一第4题
1
选择题。
利用转化的思想,通过平移把不规则的图形
转化为规则图形时,图形的面积( )。
A.扩大2倍 B.缩小2倍
C.不变 D.无法确定
C
2
判断题。
计算图形的周长时,不能运用割补或平移的方法把不规则的图形周长转化为规则图形的周长。( )
×
求这个图形的周长和面积(每个小正方形的边长是1cm)。
(5+4)×2=18(cm)
答:这个图形的周长是18cm。
3
求这个图形的周长和面积(每个小正方形的边长是1cm)。
(5+2)×2=14(cm )
答:这个图形的面积是14cm 。
3
5
( )
( )
8
2
6
2
( )
( )
3
1
( )
( )
4
1
涂色部分占整个图形的几分之几?
如图所示,在一块长26 m,宽16 m的长方形
花坛里修了一条宽2 m的曲曲折折的观赏小
路。求花坛的实际面积。
①
②
16-2
26-2
(26-2) ×(16-2)
答:花坛的实际面积是336 m 。
=24×14
=336(m )
将②先向上平移2 m,再向左平移2 m,就可以拼成一个长方形。
这节课有什么收获呢?
求一些不规则图形的周长或面积时,可以利用割补、平移等方法,将不规则图形转化成规则图形,再根据公式计算。
这节课有什么收获呢?
转化图形时,可以将部分图形进行平移,也可以对部分边进行平移。
转化后图形的周长或面积不变。
运用平移知识解决面积问题
平移
不规则图形
规则图形
转化
面积不变
