四年级下册数学人教版9.1 鸡兔同笼(课件)(共40张PPT)
文档属性
| 名称 | 四年级下册数学人教版9.1 鸡兔同笼(课件)(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:37:50 | ||
图片预览









文档简介
(共40张PPT)
第九单元 数学广角
鸡兔同笼
我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题。
情景导入
这道题的意思是:
笼子里有若干只鸡和兔。
从上面数,有35个头;
从下面数,有94只脚。
鸡和兔各有几只?
像这样已知鸡和兔的总头数和总脚数,求鸡和兔各有多少只,就是“鸡兔同笼”问题。
笼子里有若干只鸡和兔。
从上面数,有35个头;
从下面数,有94只脚。
鸡和兔各有几只?
探究新知
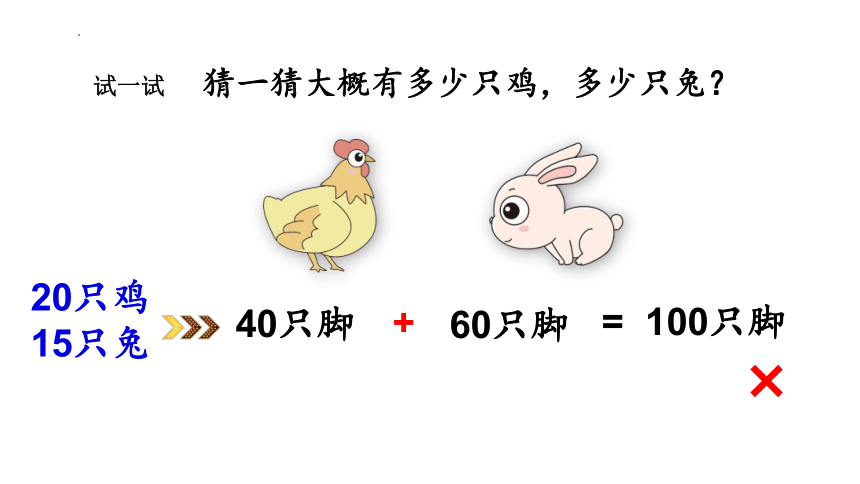
猜一猜大概有多少只鸡,多少只兔?
100只脚
20只脚
10只鸡
25只兔
+
= 120只脚
×
试一试
60只脚
40只脚
20只鸡
15只兔
+
= 100只脚
×
试一试
猜一猜大概有多少只鸡,多少只兔?
我们可以先从简单的问题入手。
你能解决这个问题吗?
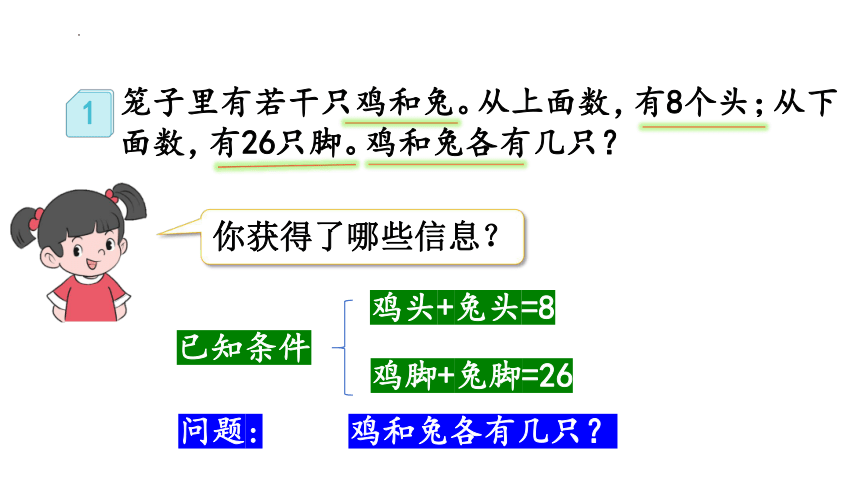
1
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。鸡和兔各有几只?
2只脚
1个头
4只脚
鸡和兔共有8只
1个头
1
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。鸡和兔各有几只?
你获得了哪些信息?
鸡头+兔头=8
鸡脚+兔脚=26
已知条件
问题:
鸡和兔各有几只?
如果有3只兔,5只鸡,那么就有3×4+5×2=22(只)脚
不对,22只<26只,说明兔的只数猜少了
如果有4只兔,4只鸡,那么就有4×4+4×2=24(只)脚
不对,24只<26只,说明兔的只数猜少了
如果有5只兔,3只鸡,那么就有5×4+3×2=26(只)脚
猜对了
方法一:猜测法
方法二:列表法
鸡
兔
脚
(1)从鸡有8只开始列举。
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
小组交流
你是怎样想的?
1.
小组同学互相交流一下。
2.
鸡
兔
脚
方法二:列表法
(2)从兔有8只开始列举。
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
8
0
32
1
7
30
2
6
28
3
5
26
鸡
兔
脚
从鸡和兔分别是总只数的一半(鸡4只、兔4只)开始列举。
(3)
4
4
24
3
5
26
方法二:列表法
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
小辉这样想:
(2)一只兔子比一只鸡多2只脚,也就是有 10÷2=5只兔。
(3)所以笼子里有3只鸡,5只兔。
(1)如果笼子里全是鸡,那么就有8×2只脚,这样就多出26-16=10只脚。
这种解题方法是假设法。
假设法
(1)假设笼子里全是鸡。
用 表示头,用 表示脚。
还差26 - 16 = 10(只)脚。
兔有5只,鸡有3只。
每次加2只脚,可以把鸡变成兔。
方法三:假设法
设鸡得兔法
兔的只数:
(26-8×2)÷(4-2)
=10÷2
=5(只)
鸡的只数:
8 - 5 = 3(只)
答:兔有5只,鸡有3只。
(1)假设笼子里全是鸡。
方法三:假设法
(2)假设笼子里全是兔。
用 表示头,用 表示脚。
还多32 - 26 = 6(只)脚。
鸡有3只,兔有5只。
每次减2只脚,可以把兔变成鸡。
方法三:假设法
设兔得鸡法
答:兔有5只,鸡有3只。
(1)假设笼子里全是兔。
鸡的只数:
(8×4-26)÷(4-2)
=6÷2
=3(只)
兔的只数:
8 - 3 = 5(只)
方法三:假设法
当用假设法解决“鸡兔同笼”问题时,假设全是鸡,先算出的是兔的只数;假设全是兔,先算出的是鸡的只数。
鸡抬起一只脚
兔抬起两只脚
1只脚
1个头
2只脚
1个头
每只鸡一只脚,每只兔子两只脚。笼子里只要有一只兔子,脚的总数就比头的总数多1。
方法三:抬脚法
脚的数量是原来的一半
26÷2=13(只)
脚的总数-头的数量=兔子的只数。
13 - 8=5(只)
鸡:8-5=3(只)
方法三:抬脚法
兔的只数:
26÷2-8
=13-8
=5(只)
鸡的只数:
8 - 5 = 3(只)
答:兔有5只,鸡有3只。
方法三:抬脚法
猜测法和列表法效率低。对于数据较大的“鸡兔同笼”问题,一般用假设法来解决,也可以用“抬脚法”来解决。
兔的只数:
(94-35×2)÷(4-2)
=24÷2
=12(只)
鸡的只数:
35-12=23(只)
答:兔有12只,鸡有23只。
方法一:假设全是鸡
你能用上面的方法解决《孙子算经》中的“鸡兔同笼”问题吗?
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
鸡的只数:
(35×4-94)÷(4-2)
=46÷2
=23(只)
兔的只数:
35-23=12(只)
答:兔有12只,鸡有23只。
方法二:假设全是兔
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
兔的只数:
94÷2-35
=47-35
=12(只)
鸡的只数:
35-12=23(只)
答:兔有12只,鸡有23只。
方法三:抬腿法
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
鸡抬起一只脚,兔子抬起两只脚。
怎样解决“鸡兔同笼”问题?
说一说
1.猜测法和列表法:适用于解决数据较小的“鸡兔同笼”问题。
怎样解决“鸡兔同笼”问题?
说一说
2.假设法:①假设全部是鸡时,兔的只数=(实际总脚数-鸡兔总只数×2)÷(4-2),鸡的总只数=鸡兔总只数-兔的只数。
怎样解决“鸡兔同笼”问题?
说一说
2.假设法:②假设全部是兔时,鸡的只数=(鸡兔总只数×4-实际总脚数)÷(4-2),兔的总只数=鸡兔总只数-鸡的只数。
怎样解决“鸡兔同笼”问题?
说一说
3.抬腿法:鸡抬起一只脚,兔子抬起两只脚。笼子里有一只兔子,脚的总数就比头的总数多1。脚的总数与头的总数之差就是兔子的只数。头的总数-兔子的只数=鸡的只数。
三轮车的数量:
(26-10×2)÷(3-2)
=(26-20)÷1
=6÷1
=6(辆)
自行车的数量:
10-6=4(辆)
答:自行车有4辆,三轮车有6辆。
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆?
1
选自教材第100页做一做
假设全是三轮车。
(3×10-26)÷(3-2)
=4÷1
=4(辆)
则三轮车有10-4=6(辆)
答:自行车有4辆,三轮车有6辆。
则一共有轮子3×10=30(个)
与实际相差30-26=4(个)
因为1辆三轮车比1辆自行车多3-2=1个轮子
由此即可求出自行车有4辆,10-4=6,所以三轮车有6辆
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆?
1
选自教材第100页做一做
选自教材第101页练习二十四第2题
2
有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?
(112-40×2)÷(4-2)
=(112-80)÷2
=32÷2
=16(只)
鹤的数量:40-16=24(只)
答:龟有16只,鹤有24只。
假设全是鹤,鹤的总脚数
鹤的总脚数与实际相差的脚数
每只龟少算了2只脚
龟的只数
兔的数量:
20-18=2(只)
答:鸡有18只,兔有2只。
鸡数量:
(20×4-44)÷(4-2)
=(80-44)÷2
=36÷2
=18(只)
有鸡兔共20只,脚44只,鸡兔各几只?
1
小船的数量:
10-7=3(只)
答:租用的大船有7只,小船有3只。
方法一:假设全
是小船
大船的数量:
(54-10×4)÷(6-4)
=(54-40)÷2
=14÷2
=7(只)
全班有54人去公园划船,一共租用了10只船,每只大船坐6人,每只小船坐4人,且所有的船刚好坐满。租用的大船和小船分别有多少只?
2
大船的数量:
10-3=7(只)
答:租用的大船有7只,小船有3只。
方法二:假设全
是大船
小船的数量:
(10×6-54)÷(6-4)
=(60-54)÷2
=6÷2
=3(只)
全班有54人去公园划船,一共租用了10只船,每只大船坐6人,每只小船坐4人,且所有的船刚好坐满。租用的大船和小船分别有多少只?
2
兔比鸡多4只,则兔比鸡多出的脚是:4×4=16只,76只减去16只是相同数量的鸡和兔一共的脚数,假设这些脚都长在鸡身上,则每只鸡有2+4=6只脚,用脚的总数除以6即可得出鸡的数量,鸡的数量加4就是兔子的数量。
鸡兔共笼,兔比鸡多4只,共有76只脚,鸡兔各几只?
兔的数量:
10+4=14(只)
答:鸡有10只,兔有14只。
鸡数量:
(76-4×4)÷(2+4)
=(76-16)÷6
=60÷6
=10(只)
鸡兔共笼,兔比鸡多4只,共有76只脚,鸡兔各几只?
这节课有什么收获呢?
鸡兔同笼问题的解题方法
3.数据较大时,用假设法比较普遍,假设全部是某一种量,先求出的就是另一种量的数量。
2.还可以用抬腿法解决。
1.数据较小时,可以用猜想法、列表法解决。
课堂小结
第九单元 数学广角
鸡兔同笼
我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题。
情景导入
这道题的意思是:
笼子里有若干只鸡和兔。
从上面数,有35个头;
从下面数,有94只脚。
鸡和兔各有几只?
像这样已知鸡和兔的总头数和总脚数,求鸡和兔各有多少只,就是“鸡兔同笼”问题。
笼子里有若干只鸡和兔。
从上面数,有35个头;
从下面数,有94只脚。
鸡和兔各有几只?
探究新知
猜一猜大概有多少只鸡,多少只兔?
100只脚
20只脚
10只鸡
25只兔
+
= 120只脚
×
试一试
60只脚
40只脚
20只鸡
15只兔
+
= 100只脚
×
试一试
猜一猜大概有多少只鸡,多少只兔?
我们可以先从简单的问题入手。
你能解决这个问题吗?
1
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。鸡和兔各有几只?
2只脚
1个头
4只脚
鸡和兔共有8只
1个头
1
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。鸡和兔各有几只?
你获得了哪些信息?
鸡头+兔头=8
鸡脚+兔脚=26
已知条件
问题:
鸡和兔各有几只?
如果有3只兔,5只鸡,那么就有3×4+5×2=22(只)脚
不对,22只<26只,说明兔的只数猜少了
如果有4只兔,4只鸡,那么就有4×4+4×2=24(只)脚
不对,24只<26只,说明兔的只数猜少了
如果有5只兔,3只鸡,那么就有5×4+3×2=26(只)脚
猜对了
方法一:猜测法
方法二:列表法
鸡
兔
脚
(1)从鸡有8只开始列举。
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
小组交流
你是怎样想的?
1.
小组同学互相交流一下。
2.
鸡
兔
脚
方法二:列表法
(2)从兔有8只开始列举。
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
8
0
32
1
7
30
2
6
28
3
5
26
鸡
兔
脚
从鸡和兔分别是总只数的一半(鸡4只、兔4只)开始列举。
(3)
4
4
24
3
5
26
方法二:列表法
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
小辉这样想:
(2)一只兔子比一只鸡多2只脚,也就是有 10÷2=5只兔。
(3)所以笼子里有3只鸡,5只兔。
(1)如果笼子里全是鸡,那么就有8×2只脚,这样就多出26-16=10只脚。
这种解题方法是假设法。
假设法
(1)假设笼子里全是鸡。
用 表示头,用 表示脚。
还差26 - 16 = 10(只)脚。
兔有5只,鸡有3只。
每次加2只脚,可以把鸡变成兔。
方法三:假设法
设鸡得兔法
兔的只数:
(26-8×2)÷(4-2)
=10÷2
=5(只)
鸡的只数:
8 - 5 = 3(只)
答:兔有5只,鸡有3只。
(1)假设笼子里全是鸡。
方法三:假设法
(2)假设笼子里全是兔。
用 表示头,用 表示脚。
还多32 - 26 = 6(只)脚。
鸡有3只,兔有5只。
每次减2只脚,可以把兔变成鸡。
方法三:假设法
设兔得鸡法
答:兔有5只,鸡有3只。
(1)假设笼子里全是兔。
鸡的只数:
(8×4-26)÷(4-2)
=6÷2
=3(只)
兔的只数:
8 - 3 = 5(只)
方法三:假设法
当用假设法解决“鸡兔同笼”问题时,假设全是鸡,先算出的是兔的只数;假设全是兔,先算出的是鸡的只数。
鸡抬起一只脚
兔抬起两只脚
1只脚
1个头
2只脚
1个头
每只鸡一只脚,每只兔子两只脚。笼子里只要有一只兔子,脚的总数就比头的总数多1。
方法三:抬脚法
脚的数量是原来的一半
26÷2=13(只)
脚的总数-头的数量=兔子的只数。
13 - 8=5(只)
鸡:8-5=3(只)
方法三:抬脚法
兔的只数:
26÷2-8
=13-8
=5(只)
鸡的只数:
8 - 5 = 3(只)
答:兔有5只,鸡有3只。
方法三:抬脚法
猜测法和列表法效率低。对于数据较大的“鸡兔同笼”问题,一般用假设法来解决,也可以用“抬脚法”来解决。
兔的只数:
(94-35×2)÷(4-2)
=24÷2
=12(只)
鸡的只数:
35-12=23(只)
答:兔有12只,鸡有23只。
方法一:假设全是鸡
你能用上面的方法解决《孙子算经》中的“鸡兔同笼”问题吗?
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
鸡的只数:
(35×4-94)÷(4-2)
=46÷2
=23(只)
兔的只数:
35-23=12(只)
答:兔有12只,鸡有23只。
方法二:假设全是兔
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
兔的只数:
94÷2-35
=47-35
=12(只)
鸡的只数:
35-12=23(只)
答:兔有12只,鸡有23只。
方法三:抬腿法
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
鸡抬起一只脚,兔子抬起两只脚。
怎样解决“鸡兔同笼”问题?
说一说
1.猜测法和列表法:适用于解决数据较小的“鸡兔同笼”问题。
怎样解决“鸡兔同笼”问题?
说一说
2.假设法:①假设全部是鸡时,兔的只数=(实际总脚数-鸡兔总只数×2)÷(4-2),鸡的总只数=鸡兔总只数-兔的只数。
怎样解决“鸡兔同笼”问题?
说一说
2.假设法:②假设全部是兔时,鸡的只数=(鸡兔总只数×4-实际总脚数)÷(4-2),兔的总只数=鸡兔总只数-鸡的只数。
怎样解决“鸡兔同笼”问题?
说一说
3.抬腿法:鸡抬起一只脚,兔子抬起两只脚。笼子里有一只兔子,脚的总数就比头的总数多1。脚的总数与头的总数之差就是兔子的只数。头的总数-兔子的只数=鸡的只数。
三轮车的数量:
(26-10×2)÷(3-2)
=(26-20)÷1
=6÷1
=6(辆)
自行车的数量:
10-6=4(辆)
答:自行车有4辆,三轮车有6辆。
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆?
1
选自教材第100页做一做
假设全是三轮车。
(3×10-26)÷(3-2)
=4÷1
=4(辆)
则三轮车有10-4=6(辆)
答:自行车有4辆,三轮车有6辆。
则一共有轮子3×10=30(个)
与实际相差30-26=4(个)
因为1辆三轮车比1辆自行车多3-2=1个轮子
由此即可求出自行车有4辆,10-4=6,所以三轮车有6辆
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆?
1
选自教材第100页做一做
选自教材第101页练习二十四第2题
2
有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?
(112-40×2)÷(4-2)
=(112-80)÷2
=32÷2
=16(只)
鹤的数量:40-16=24(只)
答:龟有16只,鹤有24只。
假设全是鹤,鹤的总脚数
鹤的总脚数与实际相差的脚数
每只龟少算了2只脚
龟的只数
兔的数量:
20-18=2(只)
答:鸡有18只,兔有2只。
鸡数量:
(20×4-44)÷(4-2)
=(80-44)÷2
=36÷2
=18(只)
有鸡兔共20只,脚44只,鸡兔各几只?
1
小船的数量:
10-7=3(只)
答:租用的大船有7只,小船有3只。
方法一:假设全
是小船
大船的数量:
(54-10×4)÷(6-4)
=(54-40)÷2
=14÷2
=7(只)
全班有54人去公园划船,一共租用了10只船,每只大船坐6人,每只小船坐4人,且所有的船刚好坐满。租用的大船和小船分别有多少只?
2
大船的数量:
10-3=7(只)
答:租用的大船有7只,小船有3只。
方法二:假设全
是大船
小船的数量:
(10×6-54)÷(6-4)
=(60-54)÷2
=6÷2
=3(只)
全班有54人去公园划船,一共租用了10只船,每只大船坐6人,每只小船坐4人,且所有的船刚好坐满。租用的大船和小船分别有多少只?
2
兔比鸡多4只,则兔比鸡多出的脚是:4×4=16只,76只减去16只是相同数量的鸡和兔一共的脚数,假设这些脚都长在鸡身上,则每只鸡有2+4=6只脚,用脚的总数除以6即可得出鸡的数量,鸡的数量加4就是兔子的数量。
鸡兔共笼,兔比鸡多4只,共有76只脚,鸡兔各几只?
兔的数量:
10+4=14(只)
答:鸡有10只,兔有14只。
鸡数量:
(76-4×4)÷(2+4)
=(76-16)÷6
=60÷6
=10(只)
鸡兔共笼,兔比鸡多4只,共有76只脚,鸡兔各几只?
这节课有什么收获呢?
鸡兔同笼问题的解题方法
3.数据较大时,用假设法比较普遍,假设全部是某一种量,先求出的就是另一种量的数量。
2.还可以用抬腿法解决。
1.数据较小时,可以用猜想法、列表法解决。
课堂小结
