2023-2024学年初中数学华东师大版八年级下册17.2.2 函数的图象 课件(共19张PPT)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册17.2.2 函数的图象 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 07:41:15 | ||
图片预览




文档简介
(共19张PPT)
17.2 函数的图象
第17章 函数及其图象
2.函数的图象
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.理解函数的图象的概念
2.掌握画函数图象的一般步骤,能画出一些简单的函数图象
3.能根据所给函数图象读出一些有用的信息
典型例题
当堂检测
学习目标
课堂总结
概念剖析
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
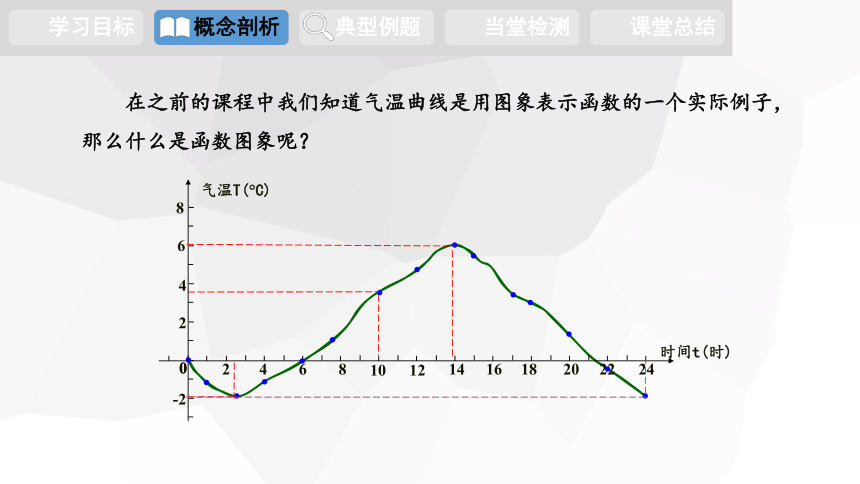
在之前的课程中我们知道气温曲线是用图象表示函数的一个实际例子,那么什么是函数图象呢?
1.图象法的相关概念:
(一)函数的图象
一般来说,函数的图象是由平面直角坐标系中一系列的点组成的.图象上每一个点的坐标(x,y)代表了函数的一组对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与该自变量对应的函数值.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
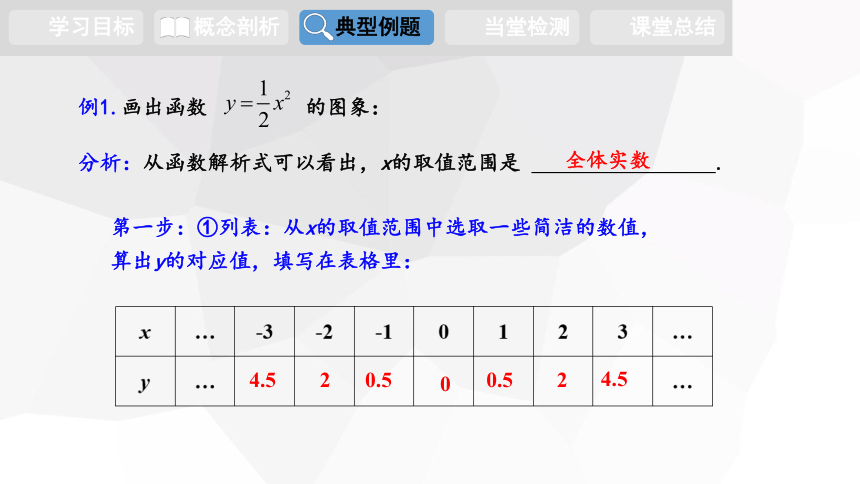
分析:从函数解析式可以看出,x的取值范围是 .
全体实数
例1.画出函数 的图象:
第一步:①列表:从x的取值范围中选取一些简洁的数值,
算出y的对应值,填写在表格里:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.5
2
0.5
0.5
2
4.5
0
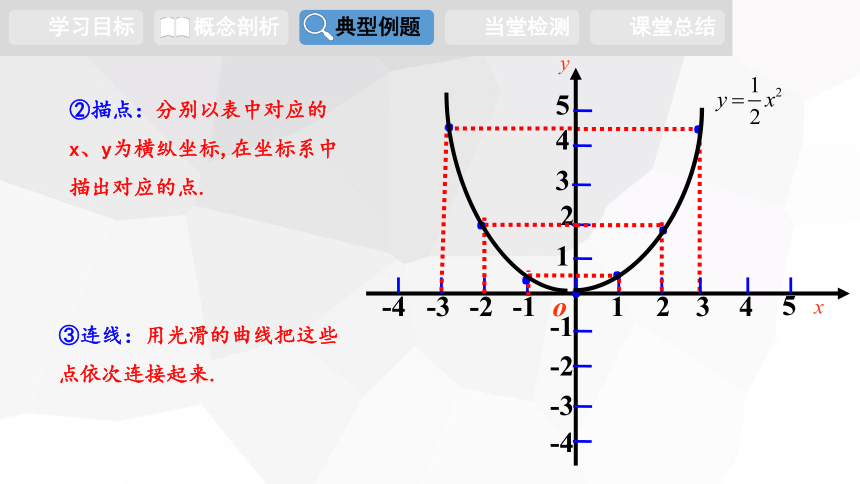
②描点:分别以表中对应的
x、y为横纵坐标,在坐标系中
描出对应的点.
·
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
·
·
·
·
·
·
③连线:用光滑的曲线把这些
点依次连接起来.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
由函数表达式画图象的一般步骤
(1)列表:
归纳总结:
给出自变量与函数的一些对应值,列表时,自变量的取值不能超出自变量的取值范围,把自变量放在表格的第一行,并按从小到大的顺序排列,相应的函数值放在第二行.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)描点:
(3)连线:按自变量从小到大的顺序,把所有的点用平滑的曲线连起来.
注意:描出的点越多,图象就越精确.
以表中自变量的值作为横坐标,对应的函数值作为纵坐标,在平面直角坐标系中描出相应的点,点取得越多,图象误差越小.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.函数y=x的图像大致是( )
A
B
C
D
A
分析:将函数y=x,按图象的一般步骤画出可大致得出图象,可以通过代入法求知,当x=1时,y=1,这个点在第一象限,x=-1时,y=-1这个点在第三象限,因此A正确.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.画出下列函数的图象:
(1) y=2x,
(2)
解:(1)函数y=2x中自变量x可为任意实数.
①列表如下:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.画出下列函数的图象:
(1) y=2x,
(2)
y=2x
②描点;
③连线.
同样可以画出函数 的图象.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.王教授和孙子小强进行了一次爬山比赛.爬山中小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)的关系(从小强开始爬山时计时).
(1)小强让爷爷先上多少米?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:由图象可知:(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米;
(3)小强通过多少时间追上爷爷
(2)山顶离山脚的距离有多少米?谁先爬上山顶?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)山顶离山脚的距离是300米,小强先爬上山;
(3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷;
3.均匀地向如图的容器中注满水,能表示在注水过程中水面高度h随时间t变化的图象是( )
A
分析:分析该容器可知:最下面的容器较粗,第二个容器最粗,那么第二阶段的函数图象水面高度h随时间t的增大而增长缓慢,用时较长,最上面容器最小,那么用时最短.故选A.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.一辆汽车由韶关匀速驶往广州,下列图象中大致能反映汽车距离广州的路程s(千米)和行驶时间t(小时)的关系的是( )
解:时间和路程不会是负值,排除A、C;由于汽车由韶关匀速驶往广州,刚出发
时距离广州的路程s应最大,并且逐步减少为0,排除D.图象B符合题意,故选B.
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.一只轮船在甲港与乙港之间往返运输,只行驶一个来回,中间经过丙港,下图是这艘轮船离开甲港的距离随时间的变化曲线.
①从甲港(O)出发到达丙港(A),需用多长时间?
解:看图可知:从甲港(0)出发到达丙港(A)需用1个小时.
②从丙港(A)到达乙港(C),需用多长时间?
从丙港(A)到达乙港(C),需用2个小时.
(1)观察曲线回答下列问题:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
③图中CD段表示什么情况,船在乙港(C)停留多长时间?返回时,多长时间到达丙港(B)?
CD段表示船在乙港(C)停留,
船在乙港停留了1个小时,
返回时4个小时到达丙港(B).
④从丙港(B)返回到出发点甲港(E),用多长时间?
从丙港(B)返回到出发点甲港(E)用了2个小时.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)轮船从甲港前往乙港的平均行驶速度快,还是轮船返回的平均速度快呢?
轮船从甲港前往乙港的平均行驶速度快.
(3)如果轮船往返的机器速度是一样的,那么从甲港到乙港是顺水还是逆水?
从甲港到乙港是顺水.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,描出表格中各数对对应的各点;
第三步,连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
1.函数图象的画法
2.从图象获取信息
17.2 函数的图象
第17章 函数及其图象
2.函数的图象
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.理解函数的图象的概念
2.掌握画函数图象的一般步骤,能画出一些简单的函数图象
3.能根据所给函数图象读出一些有用的信息
典型例题
当堂检测
学习目标
课堂总结
概念剖析
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
在之前的课程中我们知道气温曲线是用图象表示函数的一个实际例子,那么什么是函数图象呢?
1.图象法的相关概念:
(一)函数的图象
一般来说,函数的图象是由平面直角坐标系中一系列的点组成的.图象上每一个点的坐标(x,y)代表了函数的一组对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与该自变量对应的函数值.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
分析:从函数解析式可以看出,x的取值范围是 .
全体实数
例1.画出函数 的图象:
第一步:①列表:从x的取值范围中选取一些简洁的数值,
算出y的对应值,填写在表格里:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.5
2
0.5
0.5
2
4.5
0
②描点:分别以表中对应的
x、y为横纵坐标,在坐标系中
描出对应的点.
·
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
·
·
·
·
·
·
③连线:用光滑的曲线把这些
点依次连接起来.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
由函数表达式画图象的一般步骤
(1)列表:
归纳总结:
给出自变量与函数的一些对应值,列表时,自变量的取值不能超出自变量的取值范围,把自变量放在表格的第一行,并按从小到大的顺序排列,相应的函数值放在第二行.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)描点:
(3)连线:按自变量从小到大的顺序,把所有的点用平滑的曲线连起来.
注意:描出的点越多,图象就越精确.
以表中自变量的值作为横坐标,对应的函数值作为纵坐标,在平面直角坐标系中描出相应的点,点取得越多,图象误差越小.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.函数y=x的图像大致是( )
A
B
C
D
A
分析:将函数y=x,按图象的一般步骤画出可大致得出图象,可以通过代入法求知,当x=1时,y=1,这个点在第一象限,x=-1时,y=-1这个点在第三象限,因此A正确.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.画出下列函数的图象:
(1) y=2x,
(2)
解:(1)函数y=2x中自变量x可为任意实数.
①列表如下:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.画出下列函数的图象:
(1) y=2x,
(2)
y=2x
②描点;
③连线.
同样可以画出函数 的图象.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.王教授和孙子小强进行了一次爬山比赛.爬山中小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)的关系(从小强开始爬山时计时).
(1)小强让爷爷先上多少米?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:由图象可知:(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米;
(3)小强通过多少时间追上爷爷
(2)山顶离山脚的距离有多少米?谁先爬上山顶?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)山顶离山脚的距离是300米,小强先爬上山;
(3)因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷;
3.均匀地向如图的容器中注满水,能表示在注水过程中水面高度h随时间t变化的图象是( )
A
分析:分析该容器可知:最下面的容器较粗,第二个容器最粗,那么第二阶段的函数图象水面高度h随时间t的增大而增长缓慢,用时较长,最上面容器最小,那么用时最短.故选A.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.一辆汽车由韶关匀速驶往广州,下列图象中大致能反映汽车距离广州的路程s(千米)和行驶时间t(小时)的关系的是( )
解:时间和路程不会是负值,排除A、C;由于汽车由韶关匀速驶往广州,刚出发
时距离广州的路程s应最大,并且逐步减少为0,排除D.图象B符合题意,故选B.
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.一只轮船在甲港与乙港之间往返运输,只行驶一个来回,中间经过丙港,下图是这艘轮船离开甲港的距离随时间的变化曲线.
①从甲港(O)出发到达丙港(A),需用多长时间?
解:看图可知:从甲港(0)出发到达丙港(A)需用1个小时.
②从丙港(A)到达乙港(C),需用多长时间?
从丙港(A)到达乙港(C),需用2个小时.
(1)观察曲线回答下列问题:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
③图中CD段表示什么情况,船在乙港(C)停留多长时间?返回时,多长时间到达丙港(B)?
CD段表示船在乙港(C)停留,
船在乙港停留了1个小时,
返回时4个小时到达丙港(B).
④从丙港(B)返回到出发点甲港(E),用多长时间?
从丙港(B)返回到出发点甲港(E)用了2个小时.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)轮船从甲港前往乙港的平均行驶速度快,还是轮船返回的平均速度快呢?
轮船从甲港前往乙港的平均行驶速度快.
(3)如果轮船往返的机器速度是一样的,那么从甲港到乙港是顺水还是逆水?
从甲港到乙港是顺水.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,描出表格中各数对对应的各点;
第三步,连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
1.函数图象的画法
2.从图象获取信息
