2023-2024学年初中数学华东师大版八年级下册17.3.2 第1课时 一次函数图象的画法及其平移 课件(共15张PPT)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册17.3.2 第1课时 一次函数图象的画法及其平移 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 291.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 07:43:47 | ||
图片预览




文档简介
(共15张PPT)
17.3 一次函数
第17章 函数及其图象
2.一次函数的图象
第1课时 一次函数图象的画法及其平移
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.掌握一次函数图象的画法及特征
2.掌握一次函数图象平移的规律,并正确作出一次函数图象的平移
典型例题
当堂检测
学习目标
课堂总结
概念剖析
在前面课时的学习中,我们学会了正比例函数图象的画法,分为三个步骤:
①列表
②描点
③连线
那么你能用同样的方法画出一次函数的图象吗?
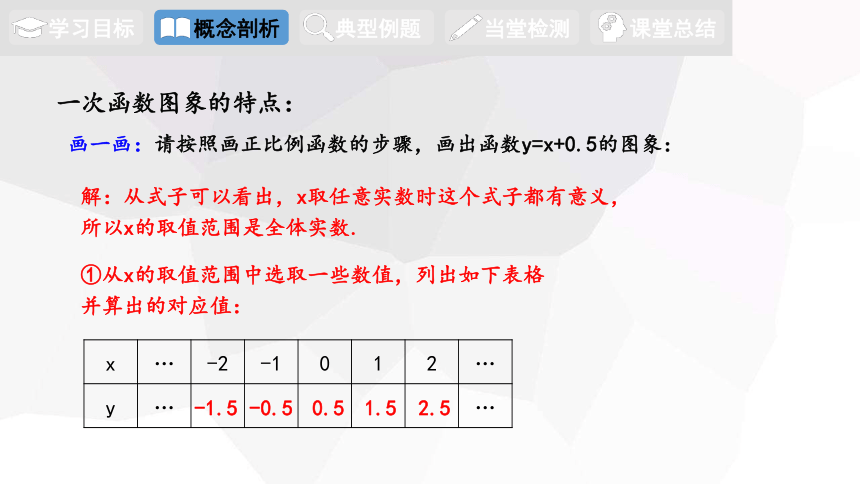
画一画:请按照画正比例函数的步骤,画出函数y=x+0.5的图象:
解:从式子可以看出,x取任意实数时这个式子都有意义,
所以x的取值范围是全体实数.
①从x的取值范围中选取一些数值,列出如下表格
并算出的对应值:
x … -2 -1 0 1 2 …
y … …
-1.5
-0.5
0.5
1.5
2.5
典型例题
当堂检测
学习目标
课堂总结
概念剖析
一次函数图象的特点:
x … -2 -1 0 1 2 …
y … …
-1.5
-0.5
0.5
1.5
2.5
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
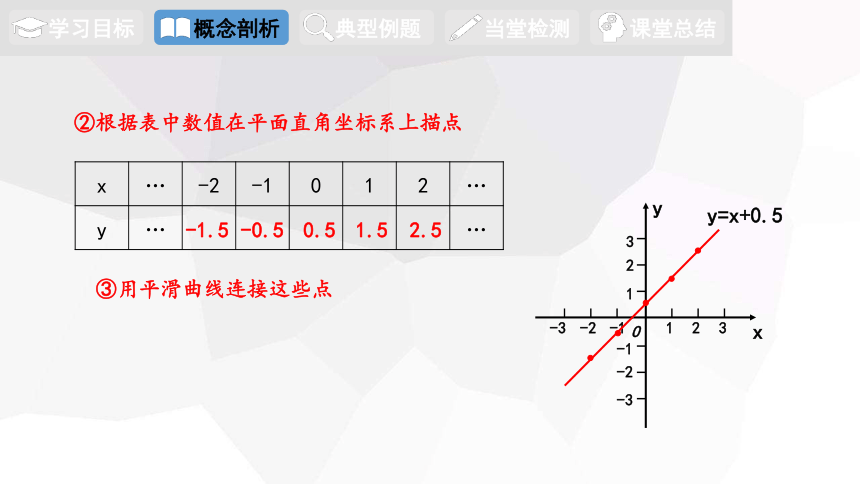
③用平滑曲线连接这些点
典型例题
当堂检测
学习目标
课堂总结
概念剖析
y=x+0.5
②根据表中数值在平面直角坐标系上描点
典型例题
当堂检测
学习目标
课堂总结
概念剖析
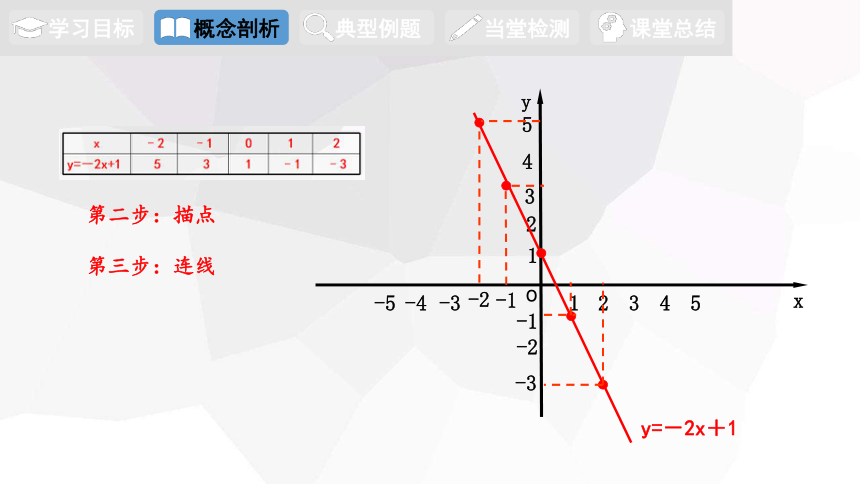
第一步:列表
x –2 –1 0 1 2
y=-2x+1 5 3 1 –1 –3
试一试:画出一次函数y=-2x+1的图象.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
-3
-2
-1
5
4
3
2
1
o
-2
-3
-4
-5
2
3
4
5
x
y
1
y=-2x+1
第三步:连线
-1
第二步:描点
典型例题
当堂检测
学习目标
课堂总结
概念剖析
观察与思考:一次函数的图象的形状是怎样的?
你能总结画一次函数
的图象的方法吗?
一次函数y=kx+b的图象也称为直线y=kx+b.
一次函数y=kx+b的图象是一条直线.
归纳总结:
(1)列表:表中给出一些自变量的值及其对应的函数值;
(2)描点:在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中的数值对应的各点;
(3)连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
画函数图象的一般步骤如下:
注意:表示x与y的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同时想象出其他点的位置.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
.
.
.
.
x
y
2
O
.
.
.
例1.已知直线y=x,如下图所示,请大家用描点法在同一坐标系内画出一次函数y=x+2,y=x-2的图象.
x … -2 -1 0 1 2 …
y=x+2 … …
y=x-2 … …
0
-3
1
-4
2
-2
3
-1
4
0
.
.
.
y=x+2
y=x-2
观察:它们的图象有什么特点?
y=x
典型例题
当堂检测
学习目标
课堂总结
概念剖析
把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1.这三个函数的图象形状都是 ,并且倾斜程度______.
2.函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移 个单位长度得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向____平移____个单位长度得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
比较三个函数的解析式, 相同,
它们的图象的位置关系是 .
自变量系数k
平行
.
.
.
.
x
y
2
O
.
.
.
.
.
.
y=x+2
y=x-2
y=x
典型例题
当堂检测
学习目标
课堂总结
概念剖析
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
总结:一次函数图象平移的规律
解析:∵一次函数y=kx+3的图像与直线y=2x平行,
∴k=2,则一次函数的表达式为y=2x+3.
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.已知一次函数y=kx+3的图像与直线y=2x平行,那么此一次函数的表达式是( )
A. y=2x+3 B. y=2x-3
C. y=-2x+3 D. y=-2x-3
2
1.一次函数 的图像过点(1,3),则m的值是 .
解析:将点(1,3)代入y=(m-1)x+2中,则3=(m-1)+2,可得m=2.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.将直线y=2x向上平移2个单位后所得图象对应的函数表达式为( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
D
4.(1)直线y=3x-2可由直线y=3x向 平移 个单位得到.
(2)直线y=x+2可由直线y=x-1向 平移 个单位得到.
下
2
上
3
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.一次函数图象的特点:
一次函数y=kx+b的图象也称为 .
一次函数y=kx+b的图象是 .
2.一次函数图象平移的规律:
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
一条直线
直线y=kx+b.
17.3 一次函数
第17章 函数及其图象
2.一次函数的图象
第1课时 一次函数图象的画法及其平移
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.掌握一次函数图象的画法及特征
2.掌握一次函数图象平移的规律,并正确作出一次函数图象的平移
典型例题
当堂检测
学习目标
课堂总结
概念剖析
在前面课时的学习中,我们学会了正比例函数图象的画法,分为三个步骤:
①列表
②描点
③连线
那么你能用同样的方法画出一次函数的图象吗?
画一画:请按照画正比例函数的步骤,画出函数y=x+0.5的图象:
解:从式子可以看出,x取任意实数时这个式子都有意义,
所以x的取值范围是全体实数.
①从x的取值范围中选取一些数值,列出如下表格
并算出的对应值:
x … -2 -1 0 1 2 …
y … …
-1.5
-0.5
0.5
1.5
2.5
典型例题
当堂检测
学习目标
课堂总结
概念剖析
一次函数图象的特点:
x … -2 -1 0 1 2 …
y … …
-1.5
-0.5
0.5
1.5
2.5
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
③用平滑曲线连接这些点
典型例题
当堂检测
学习目标
课堂总结
概念剖析
y=x+0.5
②根据表中数值在平面直角坐标系上描点
典型例题
当堂检测
学习目标
课堂总结
概念剖析
第一步:列表
x –2 –1 0 1 2
y=-2x+1 5 3 1 –1 –3
试一试:画出一次函数y=-2x+1的图象.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
-3
-2
-1
5
4
3
2
1
o
-2
-3
-4
-5
2
3
4
5
x
y
1
y=-2x+1
第三步:连线
-1
第二步:描点
典型例题
当堂检测
学习目标
课堂总结
概念剖析
观察与思考:一次函数的图象的形状是怎样的?
你能总结画一次函数
的图象的方法吗?
一次函数y=kx+b的图象也称为直线y=kx+b.
一次函数y=kx+b的图象是一条直线.
归纳总结:
(1)列表:表中给出一些自变量的值及其对应的函数值;
(2)描点:在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中的数值对应的各点;
(3)连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
画函数图象的一般步骤如下:
注意:表示x与y的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同时想象出其他点的位置.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
.
.
.
.
x
y
2
O
.
.
.
例1.已知直线y=x,如下图所示,请大家用描点法在同一坐标系内画出一次函数y=x+2,y=x-2的图象.
x … -2 -1 0 1 2 …
y=x+2 … …
y=x-2 … …
0
-3
1
-4
2
-2
3
-1
4
0
.
.
.
y=x+2
y=x-2
观察:它们的图象有什么特点?
y=x
典型例题
当堂检测
学习目标
课堂总结
概念剖析
把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1.这三个函数的图象形状都是 ,并且倾斜程度______.
2.函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移 个单位长度得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向____平移____个单位长度得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
比较三个函数的解析式, 相同,
它们的图象的位置关系是 .
自变量系数k
平行
.
.
.
.
x
y
2
O
.
.
.
.
.
.
y=x+2
y=x-2
y=x
典型例题
当堂检测
学习目标
课堂总结
概念剖析
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
总结:一次函数图象平移的规律
解析:∵一次函数y=kx+3的图像与直线y=2x平行,
∴k=2,则一次函数的表达式为y=2x+3.
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.已知一次函数y=kx+3的图像与直线y=2x平行,那么此一次函数的表达式是( )
A. y=2x+3 B. y=2x-3
C. y=-2x+3 D. y=-2x-3
2
1.一次函数 的图像过点(1,3),则m的值是 .
解析:将点(1,3)代入y=(m-1)x+2中,则3=(m-1)+2,可得m=2.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.将直线y=2x向上平移2个单位后所得图象对应的函数表达式为( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
D
4.(1)直线y=3x-2可由直线y=3x向 平移 个单位得到.
(2)直线y=x+2可由直线y=x-1向 平移 个单位得到.
下
2
上
3
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.一次函数图象的特点:
一次函数y=kx+b的图象也称为 .
一次函数y=kx+b的图象是 .
2.一次函数图象平移的规律:
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
一条直线
直线y=kx+b.
