17.5 一次函数、反比例函数的实际应用 (第3课时) 课件 20张PPT 2023-2024学年初中数学华东师大版八年级下册
文档属性
| 名称 | 17.5 一次函数、反比例函数的实际应用 (第3课时) 课件 20张PPT 2023-2024学年初中数学华东师大版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 335.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 09:15:16 | ||
图片预览







文档简介
(共20张PPT)
17.5 实践与探索
第17章 函数及其图象
3.一次函数、反比例函数的实际应用
2.能够通过分析实际问题中变量之间的关系,建立反比例函数模型解决问题,进一步提高运用函数的图象、性质的综合能力
1.能够通过分析实际问题中变量之间的关系,建立一次函数模型解决问题,进一步提高运用函数的图象、性质的综合能力
典型例题
当堂检测
学习目标
课堂总结
例1.为了研究某合金材料的体积V(cm3)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想V与t之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:V与t之间的函数关系为一次函数;
典型例题
当堂检测
学习目标
课堂总结
解:设V=kt+b(k≠0),把(10,1000.3)和(60,1002.3)代入得
解得k=0.04,b=999.9
经检验,点(-40,998.3),(-10,999.6),(0,1000),(40,1001.6)的坐标均能满足上述表达式,
V=0.04k+999.9.
所以y与x之间的函数表达式为
V=0.04k+999.9.
(2)确定V与t之间的函数表达式,并加以检验;
典型例题
当堂检测
学习目标
课堂总结
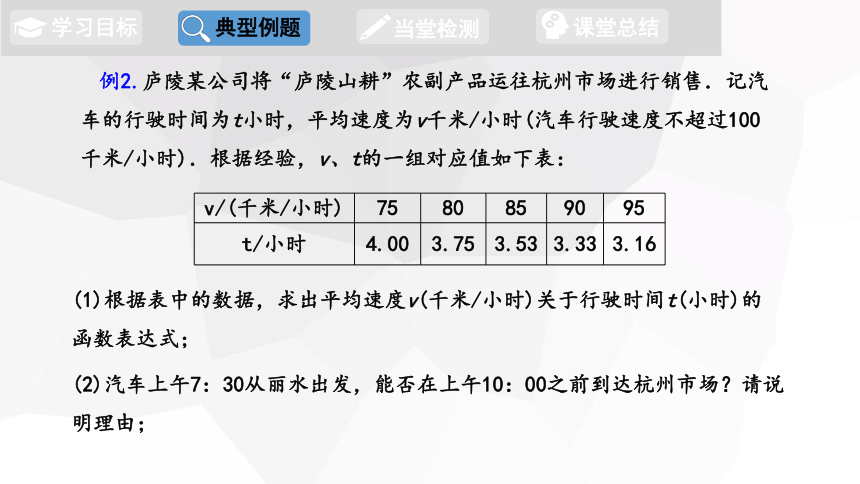
例2.庐陵某公司将“庐陵山耕”农副产品运往杭州市场进行销售.记汽车的行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v、t的一组对应值如下表:
v/(千米/小时) 75 80 85 90 95
t/小时 4.00 3.75 3.53 3.33 3.16
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
典型例题
当堂检测
学习目标
课堂总结
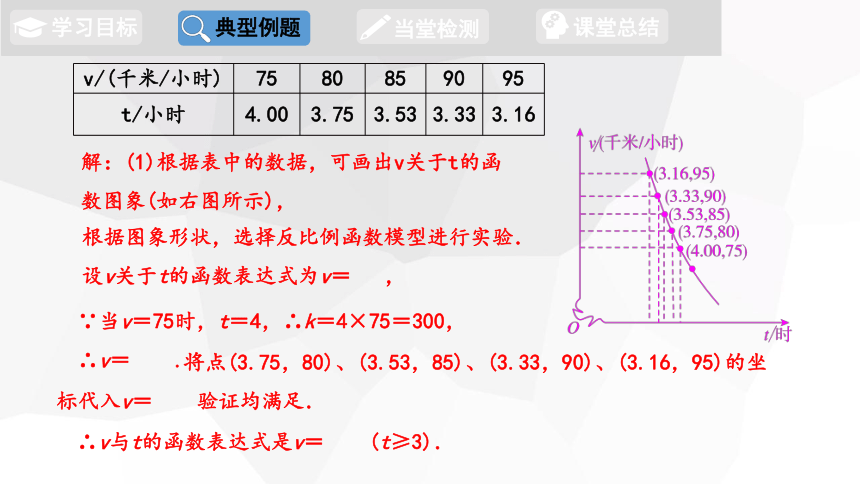
解:(1)根据表中的数据,可画出v关于t的函数图象(如右图所示),
∵当v=75时,t=4,∴k=4×75=300,
根据图象形状,选择反比例函数模型进行实验.
设v关于t的函数表达式为v= ,
将点(3.75,80)、(3.53,85)、(3.33,90)、(3.16,95)的坐标代入v= 验证均满足.
∴v与t的函数表达式是v= (t≥3).
∴v= .
v/(千米/小时) 75 80 85 90 95
t/小时 4.00 3.75 3.53 3.33 3.16
典型例题
当堂检测
学习目标
课堂总结
v/(千米/小时) 75 80 85 90 95
t/小时 4.00 3.75 3.53 3.33 3.16
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(2)∵10-7.5=2.5,
∴当t=2.5时,代入该函数表达式得v=120>100.
∴汽车上午7:30从丽水出发,不能在上午10:00之前到达杭州市场.
v与t的函数表达式是v= (t≥3).
(汽车行驶速度不超过100千米/小时)
典型例题
当堂检测
学习目标
课堂总结
方法归纳
通过上面的例题,我们知道建立两个变量之间的函数模型,可以通过下列四个步骤完成:
(4)应用这个函数模型解决问题.
(3)进行检验;
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式(一般采用待定系数法);
(1)将实验得到的数据在直角坐标系中描出;
典型例题
当堂检测
学习目标
课堂总结
温馨提示:
我们曾采用待定系数法求得一次函数和反比例函数的关系式.但是现实生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究.
典型例题
当堂检测
学习目标
课堂总结
1.当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的函数,下表记录了一组实验数据:
V(单位:m3) 1 1.5 2 2.5 3
P(单位:kPa) 96 64 48 38.4 32
P与V之间的函数关系式可能是( )
A.P=96V B.P=-16V+112
C.P=16V2-96V+176 D.
D
典型例题
当堂检测
学习目标
课堂总结
2.弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0 cm
C.物体质量每增加1 kg,弹簧长度y增加0.5 cm
D.所挂物体质量为7 kg时,弹簧长度为13.5 cm
x/kg 0 1 2 3 4 5
y/cm 10 10.5 11 11.5 12 12.5
B
典型例题
当堂检测
学习目标
课堂总结
3.为了学生的身体健康,学校课桌、凳的高度都是按一定的关系科学设计的.小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身长调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:
(1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围);
典型例题
当堂检测
学习目标
课堂总结
(1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围);
解:(1)设一次函数为y=kx+b(k≠0),将表中数据任取两组,
一次函数关系式是y=1.6x+10.8.
70=37k+b
78=42k+b
得
k=1.6, b=10.8
解得
取(37.0,70.0)和(42.0,78.0)代入,
典型例题
当堂检测
学习目标
课堂总结
(2)当x=43.5时,
(2)小明回家后,测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由.
y=1.6×43.5+10.8=80.4≠77.
答:小明家里的写字台和凳子不配套.
一次函数关系式是y=1.6x+10.8.
典型例题
当堂检测
学习目标
课堂总结
4.世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度( F)计量法.两种计量法之间有如下的对应关系:
x/℃ 0 10 20 30 40 50
y/ F 32 50 68 86 104 122
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y与x之间的函数关系为一次函数;
典型例题
当堂检测
学习目标
课堂总结
(2)确定y与x之间的函数表达式,并加以检验;
解:设y=kx+b,把(0,32)和(10,50)代入得
解得
所以y与x之间的函数表达式为
经检验,点(20,68),(30,86),(40,104),(50,122)的坐标均能满足上述表达式,
x/℃ 0 10 20 30 40 50
y/ F 32 50 68 86 104 122
典型例题
当堂检测
学习目标
课堂总结
(3)华氏0度时的温度应是多少摄氏度?
解:当y=0时,
解得
∴华氏0度时的温度应是 摄氏度;
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
解:当y=x时,
∴华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
解得
典型例题
当堂检测
学习目标
课堂总结
5.水池内原有12 m3的水,假设从排水管中每小时流出xm3的水,那么经过yh就可以把水放完.经测量,实验数据如下表:
x(x>0) … 2 4 6 8 12 …
y … 6 3 2 1.5 1 …
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条曲线上,据此,可猜想:y与x之间的函数关系为反比例函数;
典型例题
当堂检测
学习目标
课堂总结
(2)确定y与x之间的函数表达式,并加以检验;
设y关于x的函数表达式为 ,
∵当y=3时,x=4,∴k=4×3=12,
∴ .
将点(2,6)、(6,2)、(8,1.5)、(12,1)的坐标代入 验证均满足.
∴y与x的函数表达式是 .
(3)当x=6时,求y的值.
(3)把x=6代入 ,计算得到
典型例题
当堂检测
学习目标
课堂总结
函数模型的应用
①将实验得到的数据在直角坐标系中描出
②观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
典型例题
当堂检测
学习目标
课堂总结
17.5 实践与探索
第17章 函数及其图象
3.一次函数、反比例函数的实际应用
2.能够通过分析实际问题中变量之间的关系,建立反比例函数模型解决问题,进一步提高运用函数的图象、性质的综合能力
1.能够通过分析实际问题中变量之间的关系,建立一次函数模型解决问题,进一步提高运用函数的图象、性质的综合能力
典型例题
当堂检测
学习目标
课堂总结
例1.为了研究某合金材料的体积V(cm3)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想V与t之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:V与t之间的函数关系为一次函数;
典型例题
当堂检测
学习目标
课堂总结
解:设V=kt+b(k≠0),把(10,1000.3)和(60,1002.3)代入得
解得k=0.04,b=999.9
经检验,点(-40,998.3),(-10,999.6),(0,1000),(40,1001.6)的坐标均能满足上述表达式,
V=0.04k+999.9.
所以y与x之间的函数表达式为
V=0.04k+999.9.
(2)确定V与t之间的函数表达式,并加以检验;
典型例题
当堂检测
学习目标
课堂总结
例2.庐陵某公司将“庐陵山耕”农副产品运往杭州市场进行销售.记汽车的行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v、t的一组对应值如下表:
v/(千米/小时) 75 80 85 90 95
t/小时 4.00 3.75 3.53 3.33 3.16
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
典型例题
当堂检测
学习目标
课堂总结
解:(1)根据表中的数据,可画出v关于t的函数图象(如右图所示),
∵当v=75时,t=4,∴k=4×75=300,
根据图象形状,选择反比例函数模型进行实验.
设v关于t的函数表达式为v= ,
将点(3.75,80)、(3.53,85)、(3.33,90)、(3.16,95)的坐标代入v= 验证均满足.
∴v与t的函数表达式是v= (t≥3).
∴v= .
v/(千米/小时) 75 80 85 90 95
t/小时 4.00 3.75 3.53 3.33 3.16
典型例题
当堂检测
学习目标
课堂总结
v/(千米/小时) 75 80 85 90 95
t/小时 4.00 3.75 3.53 3.33 3.16
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(2)∵10-7.5=2.5,
∴当t=2.5时,代入该函数表达式得v=120>100.
∴汽车上午7:30从丽水出发,不能在上午10:00之前到达杭州市场.
v与t的函数表达式是v= (t≥3).
(汽车行驶速度不超过100千米/小时)
典型例题
当堂检测
学习目标
课堂总结
方法归纳
通过上面的例题,我们知道建立两个变量之间的函数模型,可以通过下列四个步骤完成:
(4)应用这个函数模型解决问题.
(3)进行检验;
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式(一般采用待定系数法);
(1)将实验得到的数据在直角坐标系中描出;
典型例题
当堂检测
学习目标
课堂总结
温馨提示:
我们曾采用待定系数法求得一次函数和反比例函数的关系式.但是现实生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究.
典型例题
当堂检测
学习目标
课堂总结
1.当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的函数,下表记录了一组实验数据:
V(单位:m3) 1 1.5 2 2.5 3
P(单位:kPa) 96 64 48 38.4 32
P与V之间的函数关系式可能是( )
A.P=96V B.P=-16V+112
C.P=16V2-96V+176 D.
D
典型例题
当堂检测
学习目标
课堂总结
2.弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0 cm
C.物体质量每增加1 kg,弹簧长度y增加0.5 cm
D.所挂物体质量为7 kg时,弹簧长度为13.5 cm
x/kg 0 1 2 3 4 5
y/cm 10 10.5 11 11.5 12 12.5
B
典型例题
当堂检测
学习目标
课堂总结
3.为了学生的身体健康,学校课桌、凳的高度都是按一定的关系科学设计的.小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身长调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:
(1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围);
典型例题
当堂检测
学习目标
课堂总结
(1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围);
解:(1)设一次函数为y=kx+b(k≠0),将表中数据任取两组,
一次函数关系式是y=1.6x+10.8.
70=37k+b
78=42k+b
得
k=1.6, b=10.8
解得
取(37.0,70.0)和(42.0,78.0)代入,
典型例题
当堂检测
学习目标
课堂总结
(2)当x=43.5时,
(2)小明回家后,测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由.
y=1.6×43.5+10.8=80.4≠77.
答:小明家里的写字台和凳子不配套.
一次函数关系式是y=1.6x+10.8.
典型例题
当堂检测
学习目标
课堂总结
4.世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度( F)计量法.两种计量法之间有如下的对应关系:
x/℃ 0 10 20 30 40 50
y/ F 32 50 68 86 104 122
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y与x之间的函数关系为一次函数;
典型例题
当堂检测
学习目标
课堂总结
(2)确定y与x之间的函数表达式,并加以检验;
解:设y=kx+b,把(0,32)和(10,50)代入得
解得
所以y与x之间的函数表达式为
经检验,点(20,68),(30,86),(40,104),(50,122)的坐标均能满足上述表达式,
x/℃ 0 10 20 30 40 50
y/ F 32 50 68 86 104 122
典型例题
当堂检测
学习目标
课堂总结
(3)华氏0度时的温度应是多少摄氏度?
解:当y=0时,
解得
∴华氏0度时的温度应是 摄氏度;
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
解:当y=x时,
∴华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
解得
典型例题
当堂检测
学习目标
课堂总结
5.水池内原有12 m3的水,假设从排水管中每小时流出xm3的水,那么经过yh就可以把水放完.经测量,实验数据如下表:
x(x>0) … 2 4 6 8 12 …
y … 6 3 2 1.5 1 …
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条曲线上,据此,可猜想:y与x之间的函数关系为反比例函数;
典型例题
当堂检测
学习目标
课堂总结
(2)确定y与x之间的函数表达式,并加以检验;
设y关于x的函数表达式为 ,
∵当y=3时,x=4,∴k=4×3=12,
∴ .
将点(2,6)、(6,2)、(8,1.5)、(12,1)的坐标代入 验证均满足.
∴y与x的函数表达式是 .
(3)当x=6时,求y的值.
(3)把x=6代入 ,计算得到
典型例题
当堂检测
学习目标
课堂总结
函数模型的应用
①将实验得到的数据在直角坐标系中描出
②观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
典型例题
当堂检测
学习目标
课堂总结
