18.1 平行四边形中周长与面积的相关计算习题课件 (第4课时) 15张PPT 2023-2024学年初中数学华东师大版八年级下册
文档属性
| 名称 | 18.1 平行四边形中周长与面积的相关计算习题课件 (第4课时) 15张PPT 2023-2024学年初中数学华东师大版八年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 891.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 09:24:06 | ||
图片预览




文档简介
(共15张PPT)
第4课时 平行四边形中周长与面积
的相关计算
第18章 平行四边形
18.1平行四边形的性质
1.进一步巩固平行四边形的相关性质
2.能运用平行四边形的性质求平行四边形的周长和面积
典型例题
当堂检测
学习目标
课堂总结
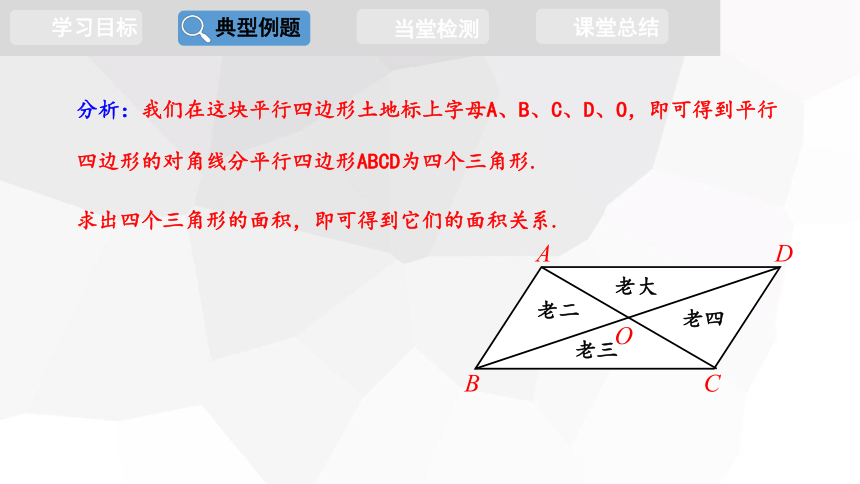
例1.在古代,有一位农夫老李,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个儿子,具体分法如下图所示.当他的四个儿子看到时,争论不休,都认为自己的地少.同学们,你认为老李这样分合理吗?为什么?
老大
老二
老四
老三
典型例题
当堂检测
学习目标
课堂总结
分析:我们在这块平行四边形土地标上字母A、B、C、D、O,即可得到平行四边形的对角线分平行四边形ABCD为四个三角形.
A
B
C
D
O
老大
老二
老三
老四
求出四个三角形的面积,即可得到它们的面积关系.
典型例题
当堂检测
学习目标
课堂总结
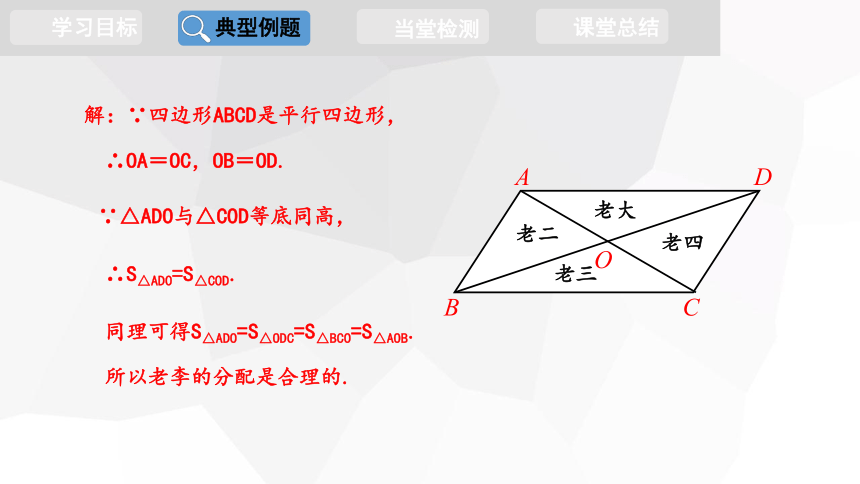
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
∴S△ADO=S△COD.
∵△ADO与△COD等底同高,
∴OA=OC,OB=OD.
解:∵四边形ABCD是平行四边形,
所以老李的分配是合理的.
A
B
C
D
O
老大
老二
老三
老四
典型例题
当堂检测
学习目标
课堂总结
平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
归纳总结
典型例题
当堂检测
学习目标
课堂总结
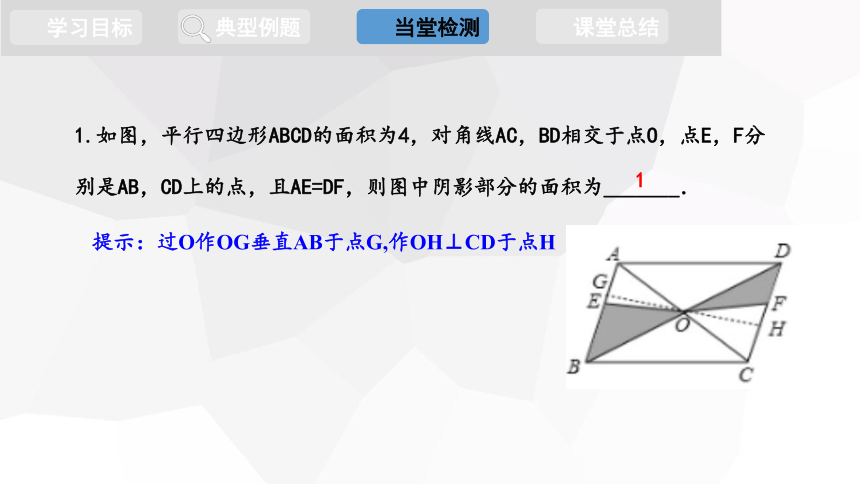
1.如图,平行四边形ABCD的面积为4,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_______.
1
典型例题
当堂检测
学习目标
课堂总结
提示:过O作OG垂直AB于点G,作OH⊥CD于点H
2.如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
点睛:已知平行四边形的高DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
则平行四边形ABCD的面积为5×16=80.
解得x=16.即AB=16.
根据平行四边形的面积公式可得5x=10(24-x),
解:设AB=x,则BC=24-x.
因为AB=16,DE=5,
典型例题
当堂检测
学习目标
课堂总结
3.如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及平行四边形ABCD的面积.
8
10
B
C
D
A
●
O
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵OA=OC
∴平行四边形面积= BC×AC=8×6=48
典型例题
当堂检测
学习目标
课堂总结
例2.如图,平行四边形ABCD的周长为16,三角形AOB的周长比三角形BOC的周长小2.求AB和BC的长.
∴AB=3,BC=5.
又∵△AOB的周长+2= △BOC的周长
解:∵四边形ABCD是平行四边形,
∴OA=OC
又∵平行四边形ABCD的周长为16,
∴AB+OA+OB+2=BC+OB+OC,即AB+2=BC.
∴2(AB+BC)=16,即4AB+4=16.
典型例题
当堂检测
学习目标
课堂总结
4.如图,□ABCD的对角线AC、BD相交于点O,且 AC+BD=20,CD=8,则△ABO的周长是( )
A. 14 B. 16 C. 18 D. 20
C
B
C
D
A
O
典型例题
当堂检测
学习目标
课堂总结
5.如图,在平行四边形ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.
5
A
B
C
D
O
典型例题
当堂检测
学习目标
课堂总结
6.如图,已知平行四边形ABCD的周长等于86cm,对角线AC与BD相交于点0,三角形AOB的周长比三角形BOC的周长大13cm,则AB=_______,BC=_______,
CD=_______,AD=_______.
7.平行四边形ABCD中,对角线AC与BD相交与点0,图中相等的线段有__________________________________若平行四边形ABCD中,AB=2AD,三角形AOB的周长比三角形AOD的周长大3cm,则平行四边形ABCD的周长=_______.
A
B
C
D
O
28cm
15cm
15cm
28cm
AB=CD AD=BC OA=OC OB=OD
18cm
典型例题
当堂检测
学习目标
课堂总结
8.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,平行四边形ABCD的周长是100cm,△AOB与△BOC的周长的和是122cm,且AC:DB= 2:1,求AC和BD的长.
解:∵四边形ABCD是平行四边形,
∴AC=48cm,BD=24cm.
又∵AC:DB=2:1,
即AC+BD=122-50=72.
∴OA+OB+AB+OB+OC+BC=122,
∵△AOB与△BOC的周长的和是122cm,
∴AB+BC=50.
∴AD=BC,AB=CD,OB=OD,
典型例题
当堂检测
学习目标
课堂总结
平行四边形中周长与面积的相关计算
平行四边形的周长=
平行四边形的面积
典型例题
当堂检测
学习目标
课堂总结
第4课时 平行四边形中周长与面积
的相关计算
第18章 平行四边形
18.1平行四边形的性质
1.进一步巩固平行四边形的相关性质
2.能运用平行四边形的性质求平行四边形的周长和面积
典型例题
当堂检测
学习目标
课堂总结
例1.在古代,有一位农夫老李,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个儿子,具体分法如下图所示.当他的四个儿子看到时,争论不休,都认为自己的地少.同学们,你认为老李这样分合理吗?为什么?
老大
老二
老四
老三
典型例题
当堂检测
学习目标
课堂总结
分析:我们在这块平行四边形土地标上字母A、B、C、D、O,即可得到平行四边形的对角线分平行四边形ABCD为四个三角形.
A
B
C
D
O
老大
老二
老三
老四
求出四个三角形的面积,即可得到它们的面积关系.
典型例题
当堂检测
学习目标
课堂总结
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
∴S△ADO=S△COD.
∵△ADO与△COD等底同高,
∴OA=OC,OB=OD.
解:∵四边形ABCD是平行四边形,
所以老李的分配是合理的.
A
B
C
D
O
老大
老二
老三
老四
典型例题
当堂检测
学习目标
课堂总结
平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
归纳总结
典型例题
当堂检测
学习目标
课堂总结
1.如图,平行四边形ABCD的面积为4,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_______.
1
典型例题
当堂检测
学习目标
课堂总结
提示:过O作OG垂直AB于点G,作OH⊥CD于点H
2.如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
点睛:已知平行四边形的高DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
则平行四边形ABCD的面积为5×16=80.
解得x=16.即AB=16.
根据平行四边形的面积公式可得5x=10(24-x),
解:设AB=x,则BC=24-x.
因为AB=16,DE=5,
典型例题
当堂检测
学习目标
课堂总结
3.如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及平行四边形ABCD的面积.
8
10
B
C
D
A
●
O
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵OA=OC
∴平行四边形面积= BC×AC=8×6=48
典型例题
当堂检测
学习目标
课堂总结
例2.如图,平行四边形ABCD的周长为16,三角形AOB的周长比三角形BOC的周长小2.求AB和BC的长.
∴AB=3,BC=5.
又∵△AOB的周长+2= △BOC的周长
解:∵四边形ABCD是平行四边形,
∴OA=OC
又∵平行四边形ABCD的周长为16,
∴AB+OA+OB+2=BC+OB+OC,即AB+2=BC.
∴2(AB+BC)=16,即4AB+4=16.
典型例题
当堂检测
学习目标
课堂总结
4.如图,□ABCD的对角线AC、BD相交于点O,且 AC+BD=20,CD=8,则△ABO的周长是( )
A. 14 B. 16 C. 18 D. 20
C
B
C
D
A
O
典型例题
当堂检测
学习目标
课堂总结
5.如图,在平行四边形ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.
5
A
B
C
D
O
典型例题
当堂检测
学习目标
课堂总结
6.如图,已知平行四边形ABCD的周长等于86cm,对角线AC与BD相交于点0,三角形AOB的周长比三角形BOC的周长大13cm,则AB=_______,BC=_______,
CD=_______,AD=_______.
7.平行四边形ABCD中,对角线AC与BD相交与点0,图中相等的线段有__________________________________若平行四边形ABCD中,AB=2AD,三角形AOB的周长比三角形AOD的周长大3cm,则平行四边形ABCD的周长=_______.
A
B
C
D
O
28cm
15cm
15cm
28cm
AB=CD AD=BC OA=OC OB=OD
18cm
典型例题
当堂检测
学习目标
课堂总结
8.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,平行四边形ABCD的周长是100cm,△AOB与△BOC的周长的和是122cm,且AC:DB= 2:1,求AC和BD的长.
解:∵四边形ABCD是平行四边形,
∴AC=48cm,BD=24cm.
又∵AC:DB=2:1,
即AC+BD=122-50=72.
∴OA+OB+AB+OB+OC+BC=122,
∵△AOB与△BOC的周长的和是122cm,
∴AB+BC=50.
∴AD=BC,AB=CD,OB=OD,
典型例题
当堂检测
学习目标
课堂总结
平行四边形中周长与面积的相关计算
平行四边形的周长=
平行四边形的面积
典型例题
当堂检测
学习目标
课堂总结
