2023-2024学年初中数学华东师大版八年级下册19.2.1 第2课时 菱形的性质与其他几何图形性质的综合 课件(共14张PPT)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册19.2.1 第2课时 菱形的性质与其他几何图形性质的综合 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
19.2.1 菱形的性质
第19章 矩形、菱形和正方形
第2课时 菱形的性质与其他几何图形性质的综合
1.运用菱形的性质求解面积和周长等问题
典型例题
当堂检测
学习目标
课堂总结
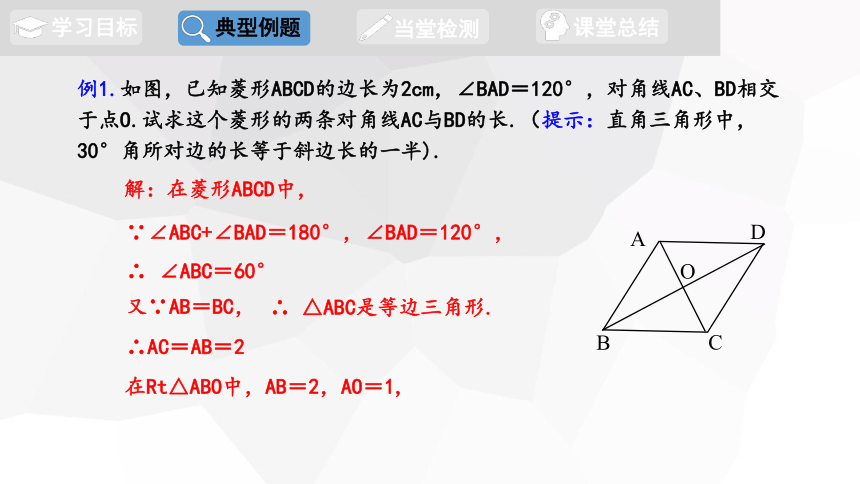
例1.如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O.试求这个菱形的两条对角线AC与BD的长.(提示:直角三角形中,30°角所对边的长等于斜边长的一半).
解:在菱形ABCD中,
在Rt△ABO中,AB=2,AO=1,
C
B
D
A
O
∴AC=AB=2
∴ △ABC是等边三角形.
又∵AB=BC,
∴ ∠ABC=60°
∵∠ABC+∠BAD=180°,∠BAD=120°,
典型例题
当堂检测
学习目标
课堂总结
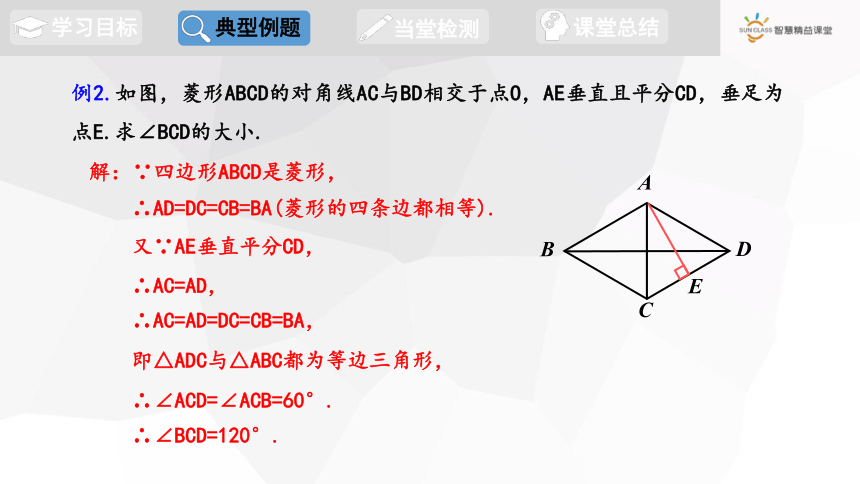
例2.如图,菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分CD,垂足为点E.求∠BCD的大小.
A
D
C
B
E
解:∵四边形ABCD是菱形,
∴∠BCD=120°.
∴∠ACD=∠ACB=60°.
即△ADC与△ABC都为等边三角形,
∴AC=AD=DC=CB=BA,
∴AC=AD,
又∵AE垂直平分CD,
∴AD=DC=CB=BA(菱形的四条边都相等).
典型例题
当堂检测
学习目标
课堂总结
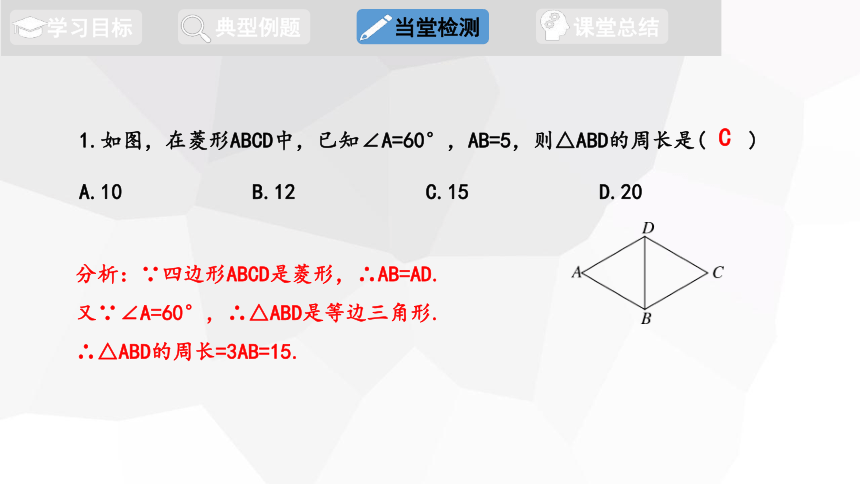
1.如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是( )
A.10 B.12 C.15 D.20
C
分析:∵四边形ABCD是菱形,∴AB=AD.
又∵∠A=60°,∴△ABD是等边三角形.
∴△ABD的周长=3AB=15.
典型例题
当堂检测
学习目标
课堂总结
2.菱形的两条对角线长分别为6和8,则菱形的周长是( )
A.40 B.24
C.20 D.10
分析:根据菱形的对角线互相垂直平分的性质,利用对角线的一半,根据勾股定理求出菱形的边长,再根据菱形的四条边相等求出周长即可.
C
典型例题
当堂检测
学习目标
课堂总结
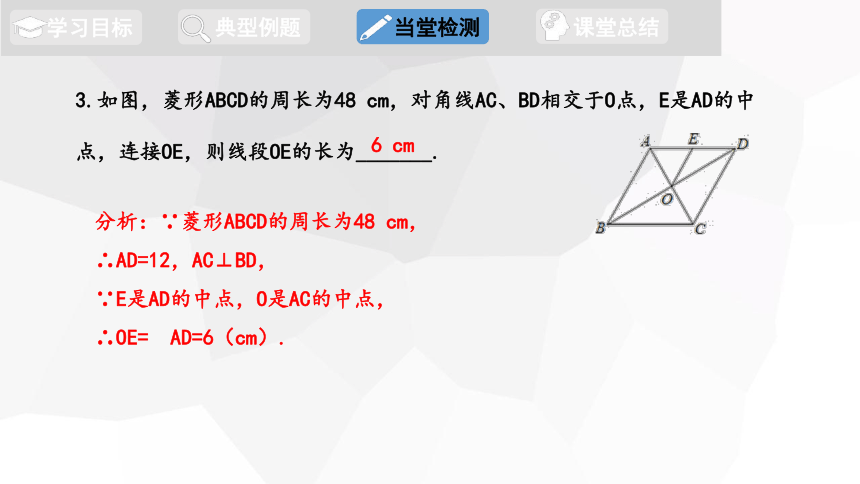
3.如图,菱形ABCD的周长为48 cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
6 cm
分析:∵菱形ABCD的周长为48 cm,
∴AD=12,AC⊥BD,
∵E是AD的中点,O是AC的中点,
∴OE= AD=6(cm).
典型例题
当堂检测
学习目标
课堂总结
例2.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果保留根号).
A
B
C
D
O
解:∵花坛ABCD是菱形,
S菱形ABCD =
典型例题
当堂检测
学习目标
课堂总结
求菱形的面积有几种
方法?你能说说你的
思路吗?
4.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为 .
30
典型例题
当堂检测
学习目标
课堂总结
5.如图,已知菱形ABCD的周长为24cm,对角线AC的长为8cm,求菱形的面积.
A
B
C
D
O
=16 (cm2)
= ×8×4
∴菱形ABCD的面积= AC·BD
∴BD=4 ,
∴OB= 2 (cm),
∵AC⊥BD,
∴OA=4cm,
∴AB=6cm,
解:∵菱形的周长为24cm,
又AC=8cm,
典型例题
当堂检测
学习目标
课堂总结
分析:设BE=x,则EC=4-x,根据勾股定理求出x的值,由菱形的性质得到EC的长,即可求出菱形AECF的面积.
解:设BE=x,则EC=4-x,
∵四边形AECF是菱形,
∴AE=EC=4-x,
在Rt△ABE中,AB +BE =AE ,即2 +x =(4-x) ,
6.如图,四边形ABCD是矩形,四边形AECF是菱形,若AB=2 cm,BC=4 cm,
求四边形AECF的面积.
解得x=1.5,
故EC=2.5,
S四边形AECF=EC·AB=2.5×2=5(cm ).
典型例题
当堂检测
学习目标
课堂总结
7.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
在直角△OCD中,由勾股定理得
∴AC⊥BD.
解:(1)∵四边形ABCD是菱形,
典型例题
当堂检测
学习目标
课堂总结
7.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(2)求四边形OBEC的面积.
∴S矩形OBEC=OB·OC=4×3=12(cm2).
∵OB=OD=3cm,
∴平行四边形OBEC为矩形.
又∵AC⊥BD,即∠COB=90°,
∴四边形OBEC为平行四边形.
(2)∵CE∥DB,BE∥AC,
典型例题
当堂检测
学习目标
课堂总结
2.菱形的面积=底×高= .
1.菱形的周长= .
与菱形有关的计算:
边长的4倍
对角线乘积的一半
典型例题
当堂检测
学习目标
课堂总结
19.2.1 菱形的性质
第19章 矩形、菱形和正方形
第2课时 菱形的性质与其他几何图形性质的综合
1.运用菱形的性质求解面积和周长等问题
典型例题
当堂检测
学习目标
课堂总结
例1.如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O.试求这个菱形的两条对角线AC与BD的长.(提示:直角三角形中,30°角所对边的长等于斜边长的一半).
解:在菱形ABCD中,
在Rt△ABO中,AB=2,AO=1,
C
B
D
A
O
∴AC=AB=2
∴ △ABC是等边三角形.
又∵AB=BC,
∴ ∠ABC=60°
∵∠ABC+∠BAD=180°,∠BAD=120°,
典型例题
当堂检测
学习目标
课堂总结
例2.如图,菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分CD,垂足为点E.求∠BCD的大小.
A
D
C
B
E
解:∵四边形ABCD是菱形,
∴∠BCD=120°.
∴∠ACD=∠ACB=60°.
即△ADC与△ABC都为等边三角形,
∴AC=AD=DC=CB=BA,
∴AC=AD,
又∵AE垂直平分CD,
∴AD=DC=CB=BA(菱形的四条边都相等).
典型例题
当堂检测
学习目标
课堂总结
1.如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是( )
A.10 B.12 C.15 D.20
C
分析:∵四边形ABCD是菱形,∴AB=AD.
又∵∠A=60°,∴△ABD是等边三角形.
∴△ABD的周长=3AB=15.
典型例题
当堂检测
学习目标
课堂总结
2.菱形的两条对角线长分别为6和8,则菱形的周长是( )
A.40 B.24
C.20 D.10
分析:根据菱形的对角线互相垂直平分的性质,利用对角线的一半,根据勾股定理求出菱形的边长,再根据菱形的四条边相等求出周长即可.
C
典型例题
当堂检测
学习目标
课堂总结
3.如图,菱形ABCD的周长为48 cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
6 cm
分析:∵菱形ABCD的周长为48 cm,
∴AD=12,AC⊥BD,
∵E是AD的中点,O是AC的中点,
∴OE= AD=6(cm).
典型例题
当堂检测
学习目标
课堂总结
例2.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果保留根号).
A
B
C
D
O
解:∵花坛ABCD是菱形,
S菱形ABCD =
典型例题
当堂检测
学习目标
课堂总结
求菱形的面积有几种
方法?你能说说你的
思路吗?
4.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为 .
30
典型例题
当堂检测
学习目标
课堂总结
5.如图,已知菱形ABCD的周长为24cm,对角线AC的长为8cm,求菱形的面积.
A
B
C
D
O
=16 (cm2)
= ×8×4
∴菱形ABCD的面积= AC·BD
∴BD=4 ,
∴OB= 2 (cm),
∵AC⊥BD,
∴OA=4cm,
∴AB=6cm,
解:∵菱形的周长为24cm,
又AC=8cm,
典型例题
当堂检测
学习目标
课堂总结
分析:设BE=x,则EC=4-x,根据勾股定理求出x的值,由菱形的性质得到EC的长,即可求出菱形AECF的面积.
解:设BE=x,则EC=4-x,
∵四边形AECF是菱形,
∴AE=EC=4-x,
在Rt△ABE中,AB +BE =AE ,即2 +x =(4-x) ,
6.如图,四边形ABCD是矩形,四边形AECF是菱形,若AB=2 cm,BC=4 cm,
求四边形AECF的面积.
解得x=1.5,
故EC=2.5,
S四边形AECF=EC·AB=2.5×2=5(cm ).
典型例题
当堂检测
学习目标
课堂总结
7.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
在直角△OCD中,由勾股定理得
∴AC⊥BD.
解:(1)∵四边形ABCD是菱形,
典型例题
当堂检测
学习目标
课堂总结
7.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(2)求四边形OBEC的面积.
∴S矩形OBEC=OB·OC=4×3=12(cm2).
∵OB=OD=3cm,
∴平行四边形OBEC为矩形.
又∵AC⊥BD,即∠COB=90°,
∴四边形OBEC为平行四边形.
(2)∵CE∥DB,BE∥AC,
典型例题
当堂检测
学习目标
课堂总结
2.菱形的面积=底×高= .
1.菱形的周长= .
与菱形有关的计算:
边长的4倍
对角线乘积的一半
典型例题
当堂检测
学习目标
课堂总结
