2023-2024学年初中数学华东师大版八年级下册19.2.2 第2课时 菱形的判定定理2 课件(共17张PPT)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册19.2.2 第2课时 菱形的判定定理2 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 09:32:39 | ||
图片预览


文档简介
(共17张PPT)
19.2 菱形
第19章 矩形、菱形与正方形
第2课时 菱形的判定定理2
2.菱形的判定
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.会利用菱形的判定定理2来判定平行四边形是否为菱形
2.能够综合运用菱形的性质与判定解题
典型例题
当堂检测
学习目标
课堂总结
概念剖析
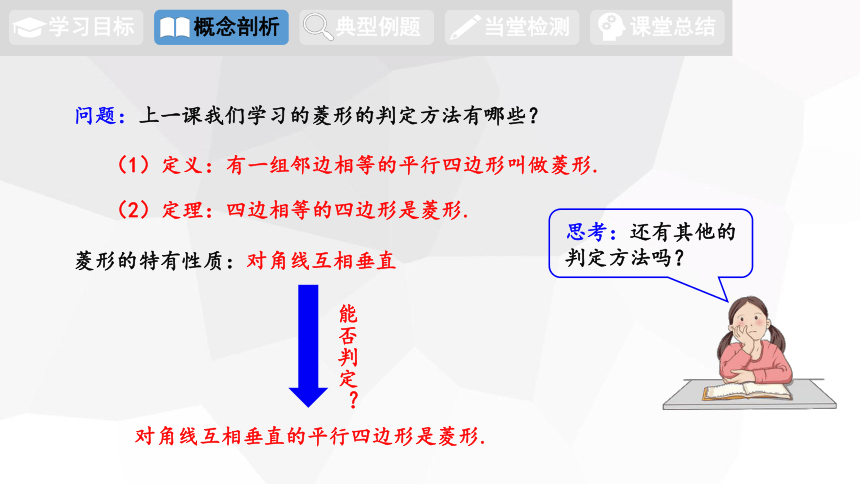
问题:上一课我们学习的菱形的判定方法有哪些?
(1)定义:有一组邻边相等的平行四边形叫做菱形.
(2)定理:四边相等的四边形是菱形.
菱形的特有性质:对角线互相垂直
对角线互相垂直的平行四边形是菱形.
能否判定?
思考:还有其他的判定方法吗?
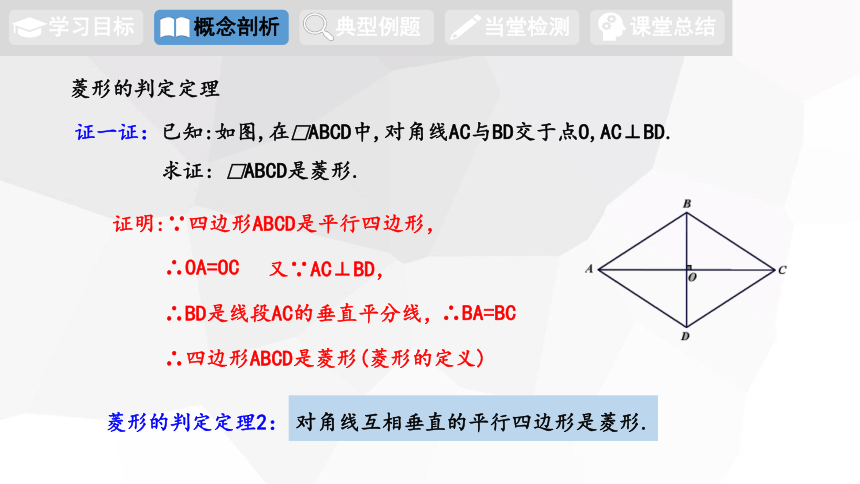
证明:∵四边形ABCD是平行四边形,
∴OA=OC
又∵AC⊥BD,
∴BD是线段AC的垂直平分线,
∴BA=BC
∴四边形ABCD是菱形(菱形的定义)
菱形的判定定理2:
对角线互相垂直的平行四边形是菱形.
证一证:已知:如图,在□ABCD中,对角线AC与BD交于点O,AC⊥BD.
求证: □ABCD是菱形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
菱形的判定定理
典型例题
当堂检测
学习目标
课堂总结
概念剖析
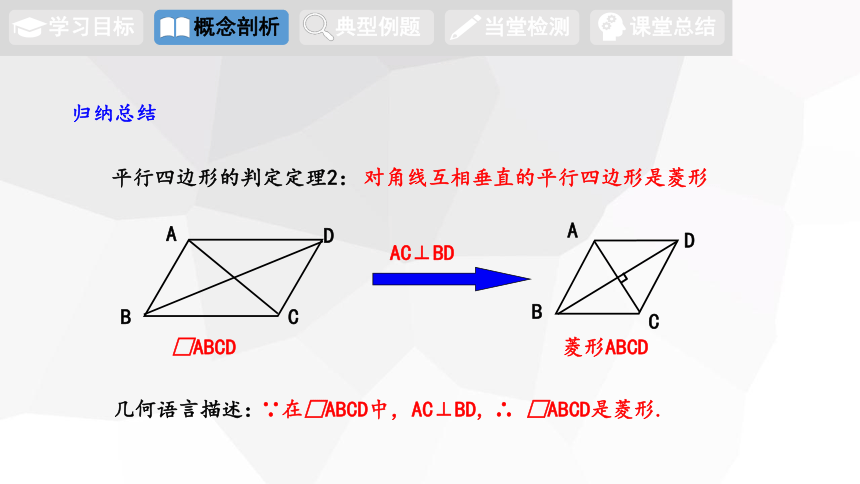
对角线互相垂直的平行四边形是菱形
AC⊥BD
∴ □ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
平行四边形的判定定理2:
归纳总结
∵在□ABCD中,AC⊥BD,
几何语言描述:
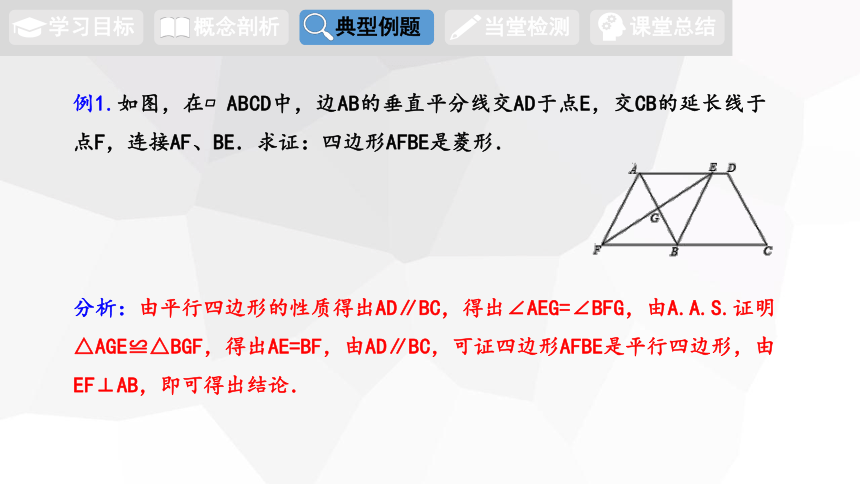
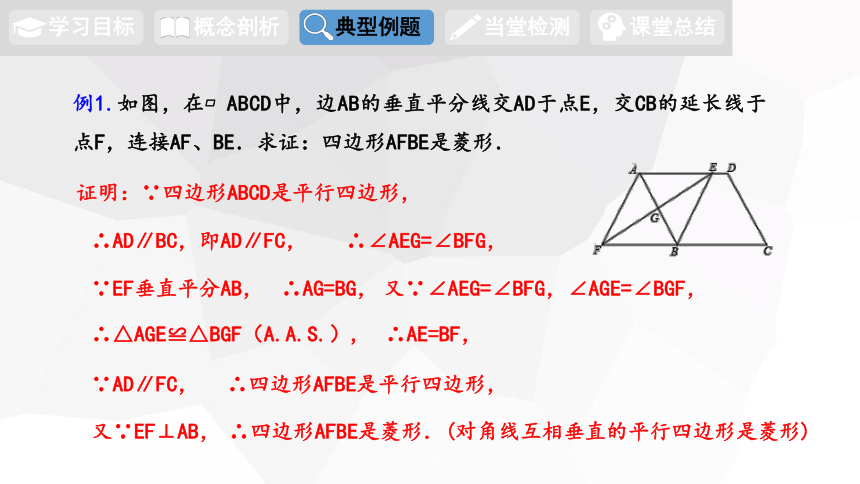
例1.如图,在 ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.求证:四边形AFBE是菱形.
分析:由平行四边形的性质得出AD∥BC,得出∠AEG=∠BFG,由A.A.S.证明△AGE≌△BGF,得出AE=BF,由AD∥BC,可证四边形AFBE是平行四边形,由EF⊥AB,即可得出结论.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AD∥FC,
∴∠AEG=∠BFG,
∵EF垂直平分AB,
∴AG=BG,
∴△AGE≌△BGF(A.A.S.),
∴AE=BF,
∵AD∥FC,
∴四边形AFBE是平行四边形,
又∵EF⊥AB,
∴四边形AFBE是菱形.(对角线互相垂直的平行四边形是菱形)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.如图,在 ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.求证:四边形AFBE是菱形.
又∵∠AEG=∠BFG,∠AGE=∠BGF,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
对角线互相垂直的平行四边形是菱形
+ 对角线互相垂直 =
总结归纳
菱形的判定方法:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90° B.AC⊥BD
C.AB=CD D.AB∥CD
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.已知平行四边形ABCD的对角线交于点O,则下列命题是假命题的是( )
A.若AC⊥BD,则平行四边形ABCD是菱形
B.若BO=2AO,则平行四边形ABCD是菱形
C.若AB=AD,则平行四边形ABCD是菱形
D.若∠ABD=∠CBD,则平行四边形ABCD是菱形
B
3.如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.求证:四边形ABCD是菱形.
A
B
C
D
O
证明:∵OA=4,OB=3,AB=5,
∴ AB =OA +OB ,
∴△AOB是直角三角形,即AC⊥BD,
∴四边形ABCD是菱形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形.
又∵EF⊥GH,
∴四边形EGFH是平行四边形,
∴△AGE≌△FHC(S.A.S.),
AE=CF,∠A=∠C,AG=CH,
在△AGE和△FHC中,
∵DH=BG,
∴AB=CD,∠A=∠C,
解:∵四边形ABCD是平行四边形,
∴四边形EGFH是菱形.
∴AG=CH,
∴GE=FH,
同理GF=EH,
例2.如图,在 ABCD中,AC平分∠DAB,AB=2,求 ABCD的周长.
点拨:求 ABCD的周长可先证明 ABCD是菱形.
解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,
又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACB=∠BAC,
∴平行四边形ABCD为菱形(有一组邻边相等的平行四边形是菱形)
又∵AB=2,
∴AD∥BC,
∴AB=BC,
∴四边形ABCD的周长=4×2=8.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解决这类与菱形相关的几何问题时,往往需要先根据题中给出的已知条件选择合适的判定方法证明四边形为菱形,最后再结合菱形的性质求解.
方法归纳总结:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.如图,在平行四边形ABCD中,AC = 6,BD = 8,AD = 5. 求AB的长.
解: ∵ 四边形ABCD为平行四边形,
∴ △DAO是直角三角形.
∴ ∠DOA = 90°,即DB⊥AC.
∴ 平行四边形ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)
∴
又∵ AD=5,满足
∴ AB=AD=5 .
6.一个平行四边形的一条边长是9,两条对角线的长分别是12和 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
是特殊的平行四边形,
A
B
C
D
O
理由:如右图, ABCD中,AC= ,BD=12,AD=9,
∵平行四边形对角线互相平分,
∴OA=0C= ,OD=OB=6,
∵62 + =92,
∴△AOD是直角三角形,AO⊥DO,
∴AC⊥BD,
∴四边形ABCD是菱形,是特殊的平行四边形
S菱形ABCD= BD·AC= ×12× =
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
两组对边分别平行或相等
四边形
平行四边形
两组对角分别相等
19.2 菱形
第19章 矩形、菱形与正方形
第2课时 菱形的判定定理2
2.菱形的判定
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.会利用菱形的判定定理2来判定平行四边形是否为菱形
2.能够综合运用菱形的性质与判定解题
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题:上一课我们学习的菱形的判定方法有哪些?
(1)定义:有一组邻边相等的平行四边形叫做菱形.
(2)定理:四边相等的四边形是菱形.
菱形的特有性质:对角线互相垂直
对角线互相垂直的平行四边形是菱形.
能否判定?
思考:还有其他的判定方法吗?
证明:∵四边形ABCD是平行四边形,
∴OA=OC
又∵AC⊥BD,
∴BD是线段AC的垂直平分线,
∴BA=BC
∴四边形ABCD是菱形(菱形的定义)
菱形的判定定理2:
对角线互相垂直的平行四边形是菱形.
证一证:已知:如图,在□ABCD中,对角线AC与BD交于点O,AC⊥BD.
求证: □ABCD是菱形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
菱形的判定定理
典型例题
当堂检测
学习目标
课堂总结
概念剖析
对角线互相垂直的平行四边形是菱形
AC⊥BD
∴ □ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
平行四边形的判定定理2:
归纳总结
∵在□ABCD中,AC⊥BD,
几何语言描述:
例1.如图,在 ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.求证:四边形AFBE是菱形.
分析:由平行四边形的性质得出AD∥BC,得出∠AEG=∠BFG,由A.A.S.证明△AGE≌△BGF,得出AE=BF,由AD∥BC,可证四边形AFBE是平行四边形,由EF⊥AB,即可得出结论.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AD∥FC,
∴∠AEG=∠BFG,
∵EF垂直平分AB,
∴AG=BG,
∴△AGE≌△BGF(A.A.S.),
∴AE=BF,
∵AD∥FC,
∴四边形AFBE是平行四边形,
又∵EF⊥AB,
∴四边形AFBE是菱形.(对角线互相垂直的平行四边形是菱形)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.如图,在 ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.求证:四边形AFBE是菱形.
又∵∠AEG=∠BFG,∠AGE=∠BGF,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
对角线互相垂直的平行四边形是菱形
+ 对角线互相垂直 =
总结归纳
菱形的判定方法:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90° B.AC⊥BD
C.AB=CD D.AB∥CD
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.已知平行四边形ABCD的对角线交于点O,则下列命题是假命题的是( )
A.若AC⊥BD,则平行四边形ABCD是菱形
B.若BO=2AO,则平行四边形ABCD是菱形
C.若AB=AD,则平行四边形ABCD是菱形
D.若∠ABD=∠CBD,则平行四边形ABCD是菱形
B
3.如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.求证:四边形ABCD是菱形.
A
B
C
D
O
证明:∵OA=4,OB=3,AB=5,
∴ AB =OA +OB ,
∴△AOB是直角三角形,即AC⊥BD,
∴四边形ABCD是菱形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形.
又∵EF⊥GH,
∴四边形EGFH是平行四边形,
∴△AGE≌△FHC(S.A.S.),
AE=CF,∠A=∠C,AG=CH,
在△AGE和△FHC中,
∵DH=BG,
∴AB=CD,∠A=∠C,
解:∵四边形ABCD是平行四边形,
∴四边形EGFH是菱形.
∴AG=CH,
∴GE=FH,
同理GF=EH,
例2.如图,在 ABCD中,AC平分∠DAB,AB=2,求 ABCD的周长.
点拨:求 ABCD的周长可先证明 ABCD是菱形.
解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,
又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACB=∠BAC,
∴平行四边形ABCD为菱形(有一组邻边相等的平行四边形是菱形)
又∵AB=2,
∴AD∥BC,
∴AB=BC,
∴四边形ABCD的周长=4×2=8.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解决这类与菱形相关的几何问题时,往往需要先根据题中给出的已知条件选择合适的判定方法证明四边形为菱形,最后再结合菱形的性质求解.
方法归纳总结:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.如图,在平行四边形ABCD中,AC = 6,BD = 8,AD = 5. 求AB的长.
解: ∵ 四边形ABCD为平行四边形,
∴ △DAO是直角三角形.
∴ ∠DOA = 90°,即DB⊥AC.
∴ 平行四边形ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)
∴
又∵ AD=5,满足
∴ AB=AD=5 .
6.一个平行四边形的一条边长是9,两条对角线的长分别是12和 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
是特殊的平行四边形,
A
B
C
D
O
理由:如右图, ABCD中,AC= ,BD=12,AD=9,
∵平行四边形对角线互相平分,
∴OA=0C= ,OD=OB=6,
∵62 + =92,
∴△AOD是直角三角形,AO⊥DO,
∴AC⊥BD,
∴四边形ABCD是菱形,是特殊的平行四边形
S菱形ABCD= BD·AC= ×12× =
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
两组对边分别平行或相等
四边形
平行四边形
两组对角分别相等
