2023-2024学年初中数学华东师大版八年级下册20.2.1 中位数与众数 课件 (共20张PPT)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册20.2.1 中位数与众数 课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 306.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 09:35:45 | ||
图片预览







文档简介
(共20张PPT)
20.2 数据的集中趋势
第20章 数据的整理与初步处理
1.中位数和众数
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.理解中位数、众数的概念,会求一组数据的中位数、众数
2.掌握中位数、众数的作用,会用中位数、众数分析实际问题
典型例题
当堂检测
学习目标
课堂总结
概念剖析
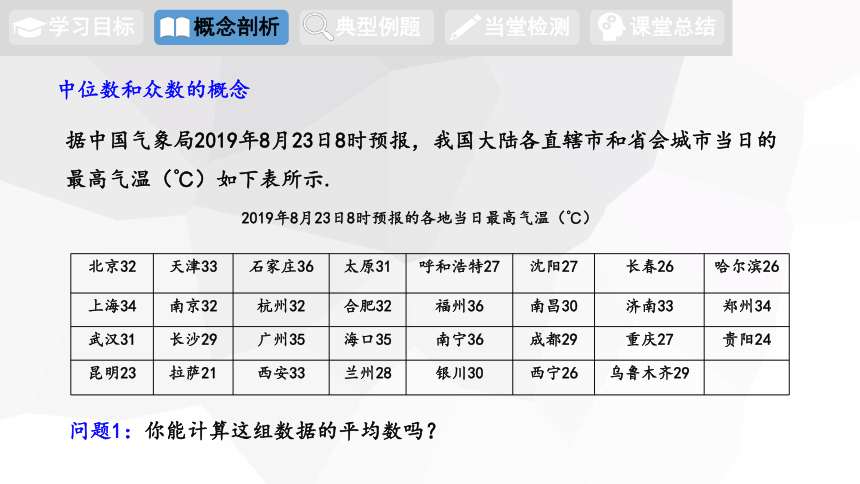
据中国气象局2019年8月23日8时预报,我国大陆各直辖市和省会城市当日的最高气温(℃)如下表所示.
2019年8月23日8时预报的各地当日最高气温(℃)
北京32 天津33 石家庄36 太原31 呼和浩特27 沈阳27 长春26 哈尔滨26
上海34 南京32 杭州32 合肥32 福州36 南昌30 济南33 郑州34
武汉31 长沙29 广州35 海口35 南宁36 成都29 重庆27 贵阳24
昆明23 拉萨21 西安33 兰州28 银川30 西宁26 乌鲁木齐29
问题1:你能计算这组数据的平均数吗?
中位数和众数的概念
典型例题
当堂检测
学习目标
课堂总结
概念剖析
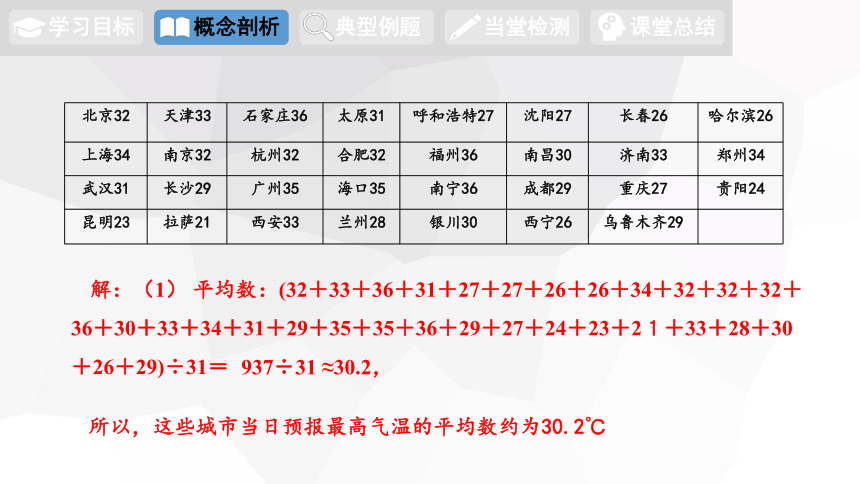
北京32 天津33 石家庄36 太原31 呼和浩特27 沈阳27 长春26 哈尔滨26
上海34 南京32 杭州32 合肥32 福州36 南昌30 济南33 郑州34
武汉31 长沙29 广州35 海口35 南宁36 成都29 重庆27 贵阳24
昆明23 拉萨21 西安33 兰州28 银川30 西宁26 乌鲁木齐29
解:(1) 平均数:(32+33+36+31+27+27+26+26+34+32+32+32+36+30+33+34+31+29+35+35+36+29+27+24+23+21+33+28+30+26+29)÷31=
所以,这些城市当日预报最高气温的平均数约为30.2℃
937÷31 ≈30.2,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如下图,将31个城市的气温数据按由低到高的顺序重新排列,用去掉两端逐步接近正中心的办法可以找出处在正中间位置的那个值,即中位数.
所以,这些城市当日预报最高气温的中位数是31℃.
问题2:你知道这组数的中位数怎么计算吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思 考1:如果是偶数个城市,那么用去掉两端逐步接近正中心的办法,最后剩下的数据是唯一一个没被划去的数据吗?
如果是偶数个城市,那么最后就将剩下两个处在正中间的数,这时,为了公正起见,我们取这两个数的算术平均数作为中位数.
比如:数据1、2、3、4、5、6的中位数是:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如上表,统计每一气温在31个城市预报最高气温数据中出现的频数,可以找出频数最多的那个气温值,它就是众数.
气温℃ 21 23 24 26 27 28 29 30 31 32 33 34 35 36
频数 1 1 1 3 3 1 3 2 2 4 3 2 2 3
由表可知,这些城市当日预报最高气温的众数是32℃.
问题3:你知道如何计算下面这组数的众数吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思 考2:若有两个气温(如29℃和32℃)的频数并列最多,那么怎样决定众数呢
如果这样,那么我们不是取29℃和32℃这两个数的平均数作为众数,而是说这两个气温值都是众数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
总结归纳:
平均数:反映了这组数据中各数据的平均大小.
中位数:如果将一组数据按由小到大的顺序排列(即使有相等的数据也要全部参加排列),那么中位数的左边和右边恰有一样多的数据.
众数:众数告诉我们,这个值出现的次数最多.一组数据可以有不止一个众数,也可以没有众数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.(1)求下列各组数据的中位数.
①10,5,6,7,4,11; ②6,6,6,8,8,10,10,7,7,12,12;
分析:先把各组数据按照从小到大顺序排列,再根据中位数定义求中位数.
解:①中数据排序后为:4,5,6,7,10,11,数据的个数为偶数(6个);
故中位数为6和7的平均数,即(6+7)÷2=6.5.
②中数据排序后为:6,6,6,7,7,8,8,10,10,12,12,数据的个数为奇数(11个);
取中间位置的数,故中位数为8.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.(2)若一组数据18,22,15,13,x,7,它的中位数是16,求x的值.
分析:先把各组数据(除x外)按照从小到大顺序排列,然后分析x所在位置;
最后根据已知条件求出x的值.
解:数据不带x排序后为:7,13,15,18,22;
当15和18是中间位置时,(15+18)÷2=16.5≠16,故不成立.
所以中间位置为15和x.
根据题意得(15+x)÷2=16,解得x=17.故x的值为17.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
方法归纳:
确定一组数据的中位数的步骤:
(1)排序,由大到小或由小到大;
(2)确定数据的个数是奇数个还是偶数个;
(3)如果是奇数个数据,中间的数据就是中位数,
如果是偶数个数据,中位数是中间两个数据的平均数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,
求x值及这组数据的中位数.
解:∵10,10,x,8的中位数与平均数相等,
∴x是8,这组数据的中位数是9.
中位数:(10+x)÷2=9,
∴(10+x)÷2=(10+10+x+8)÷4,解得x=8,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.下面的条形图描述了某车间工人日加工零件数的情况.
0
2
4
6
8
10
3
4
5
6
7
8
日加工零件数
人数
请找出这些工人日加工零件数的中位数,并说明这个中位数的意义.
解:共有36个数,中间位置的是6和6,因而中位数是6.
在这些工人中,有一半工人的日加工零件数大于或等于6个,
有一半工人加工零件数小于或等于6 个.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示:
你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
分析:一般来讲,鞋店比较关心哪种尺码的鞋销量最大,也就是关心卖出的鞋的尺码组成的一组数据的众数,一段时间内卖出的30双女鞋的尺码组成一个样本数据,通过分析样本数据可以找出样本数据的众数,进而可以估计这家鞋店销售哪种尺码的鞋最多.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示:
你能根据表中的数据为这家鞋店提供进货建议吗?
解:观察数据可知23.5出现次数最多,
故建议商家多进23.5码的这种女鞋.
即众数为23.5.
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
思考:分析表中的数据,你还能为鞋店进货提出哪些建议?
参考:22、22.5、24.5、25码的这四种鞋应该少进.
3.已知一组数据从小到大依次为-1,0,4,x,6,15,其中位数为5,则其众数为( )
A. 4 B. 5 C. 5.5 D. 6
解析:根据题目可知数据已排序,
则取最中间两个数4、x的平均数,所以(4+x)/2=5
可得x=6,
故该组数据的众数为6.
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.一名警察在高速公路上随机观察了6辆过往车辆,它们的车速分别为(单位:千米/时): 66, 57, 71, 54, 69, 58.
那么,这6辆车车速的中位数和众数是什么呢
解:将6辆车的速度按从小到大的顺序重新排列,得到
54, 57, 58, 66, 69, 71.
位于正中间的数值不是一个而是两个,所以应取这两个数值的平均数作为中位数,即中位数是(58+66)÷2=62(千米/时)
因为每辆车的速度都不一样,没有哪个车速出现的次数比别的多,所以这6辆车的速度没有众数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.某校男子足球队的年龄分布如条形图所示,请找出这些年龄的平均数、
众数、中位数,解释它们的含义.
人数
年龄
平均数:
=15(岁).
中位数:15岁.
众数:15岁.
该足球队平均年龄为15岁,处在中间位置的年龄也是15岁,15岁的人数也是最多的.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
中位数和众数
中位数:中间的一个数,或中间的两个数的平均数.
众数:出现次数最多的数.
平均数、中位数、众数的特征:平均数是最常用的指标,它表示“一般水平”,中位数表示“中等水平”,众数表示“多数水平”.
20.2 数据的集中趋势
第20章 数据的整理与初步处理
1.中位数和众数
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.理解中位数、众数的概念,会求一组数据的中位数、众数
2.掌握中位数、众数的作用,会用中位数、众数分析实际问题
典型例题
当堂检测
学习目标
课堂总结
概念剖析
据中国气象局2019年8月23日8时预报,我国大陆各直辖市和省会城市当日的最高气温(℃)如下表所示.
2019年8月23日8时预报的各地当日最高气温(℃)
北京32 天津33 石家庄36 太原31 呼和浩特27 沈阳27 长春26 哈尔滨26
上海34 南京32 杭州32 合肥32 福州36 南昌30 济南33 郑州34
武汉31 长沙29 广州35 海口35 南宁36 成都29 重庆27 贵阳24
昆明23 拉萨21 西安33 兰州28 银川30 西宁26 乌鲁木齐29
问题1:你能计算这组数据的平均数吗?
中位数和众数的概念
典型例题
当堂检测
学习目标
课堂总结
概念剖析
北京32 天津33 石家庄36 太原31 呼和浩特27 沈阳27 长春26 哈尔滨26
上海34 南京32 杭州32 合肥32 福州36 南昌30 济南33 郑州34
武汉31 长沙29 广州35 海口35 南宁36 成都29 重庆27 贵阳24
昆明23 拉萨21 西安33 兰州28 银川30 西宁26 乌鲁木齐29
解:(1) 平均数:(32+33+36+31+27+27+26+26+34+32+32+32+36+30+33+34+31+29+35+35+36+29+27+24+23+21+33+28+30+26+29)÷31=
所以,这些城市当日预报最高气温的平均数约为30.2℃
937÷31 ≈30.2,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如下图,将31个城市的气温数据按由低到高的顺序重新排列,用去掉两端逐步接近正中心的办法可以找出处在正中间位置的那个值,即中位数.
所以,这些城市当日预报最高气温的中位数是31℃.
问题2:你知道这组数的中位数怎么计算吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思 考1:如果是偶数个城市,那么用去掉两端逐步接近正中心的办法,最后剩下的数据是唯一一个没被划去的数据吗?
如果是偶数个城市,那么最后就将剩下两个处在正中间的数,这时,为了公正起见,我们取这两个数的算术平均数作为中位数.
比如:数据1、2、3、4、5、6的中位数是:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如上表,统计每一气温在31个城市预报最高气温数据中出现的频数,可以找出频数最多的那个气温值,它就是众数.
气温℃ 21 23 24 26 27 28 29 30 31 32 33 34 35 36
频数 1 1 1 3 3 1 3 2 2 4 3 2 2 3
由表可知,这些城市当日预报最高气温的众数是32℃.
问题3:你知道如何计算下面这组数的众数吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思 考2:若有两个气温(如29℃和32℃)的频数并列最多,那么怎样决定众数呢
如果这样,那么我们不是取29℃和32℃这两个数的平均数作为众数,而是说这两个气温值都是众数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
总结归纳:
平均数:反映了这组数据中各数据的平均大小.
中位数:如果将一组数据按由小到大的顺序排列(即使有相等的数据也要全部参加排列),那么中位数的左边和右边恰有一样多的数据.
众数:众数告诉我们,这个值出现的次数最多.一组数据可以有不止一个众数,也可以没有众数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.(1)求下列各组数据的中位数.
①10,5,6,7,4,11; ②6,6,6,8,8,10,10,7,7,12,12;
分析:先把各组数据按照从小到大顺序排列,再根据中位数定义求中位数.
解:①中数据排序后为:4,5,6,7,10,11,数据的个数为偶数(6个);
故中位数为6和7的平均数,即(6+7)÷2=6.5.
②中数据排序后为:6,6,6,7,7,8,8,10,10,12,12,数据的个数为奇数(11个);
取中间位置的数,故中位数为8.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.(2)若一组数据18,22,15,13,x,7,它的中位数是16,求x的值.
分析:先把各组数据(除x外)按照从小到大顺序排列,然后分析x所在位置;
最后根据已知条件求出x的值.
解:数据不带x排序后为:7,13,15,18,22;
当15和18是中间位置时,(15+18)÷2=16.5≠16,故不成立.
所以中间位置为15和x.
根据题意得(15+x)÷2=16,解得x=17.故x的值为17.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
方法归纳:
确定一组数据的中位数的步骤:
(1)排序,由大到小或由小到大;
(2)确定数据的个数是奇数个还是偶数个;
(3)如果是奇数个数据,中间的数据就是中位数,
如果是偶数个数据,中位数是中间两个数据的平均数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,
求x值及这组数据的中位数.
解:∵10,10,x,8的中位数与平均数相等,
∴x是8,这组数据的中位数是9.
中位数:(10+x)÷2=9,
∴(10+x)÷2=(10+10+x+8)÷4,解得x=8,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.下面的条形图描述了某车间工人日加工零件数的情况.
0
2
4
6
8
10
3
4
5
6
7
8
日加工零件数
人数
请找出这些工人日加工零件数的中位数,并说明这个中位数的意义.
解:共有36个数,中间位置的是6和6,因而中位数是6.
在这些工人中,有一半工人的日加工零件数大于或等于6个,
有一半工人加工零件数小于或等于6 个.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示:
你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
分析:一般来讲,鞋店比较关心哪种尺码的鞋销量最大,也就是关心卖出的鞋的尺码组成的一组数据的众数,一段时间内卖出的30双女鞋的尺码组成一个样本数据,通过分析样本数据可以找出样本数据的众数,进而可以估计这家鞋店销售哪种尺码的鞋最多.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示:
你能根据表中的数据为这家鞋店提供进货建议吗?
解:观察数据可知23.5出现次数最多,
故建议商家多进23.5码的这种女鞋.
即众数为23.5.
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
思考:分析表中的数据,你还能为鞋店进货提出哪些建议?
参考:22、22.5、24.5、25码的这四种鞋应该少进.
3.已知一组数据从小到大依次为-1,0,4,x,6,15,其中位数为5,则其众数为( )
A. 4 B. 5 C. 5.5 D. 6
解析:根据题目可知数据已排序,
则取最中间两个数4、x的平均数,所以(4+x)/2=5
可得x=6,
故该组数据的众数为6.
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.一名警察在高速公路上随机观察了6辆过往车辆,它们的车速分别为(单位:千米/时): 66, 57, 71, 54, 69, 58.
那么,这6辆车车速的中位数和众数是什么呢
解:将6辆车的速度按从小到大的顺序重新排列,得到
54, 57, 58, 66, 69, 71.
位于正中间的数值不是一个而是两个,所以应取这两个数值的平均数作为中位数,即中位数是(58+66)÷2=62(千米/时)
因为每辆车的速度都不一样,没有哪个车速出现的次数比别的多,所以这6辆车的速度没有众数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.某校男子足球队的年龄分布如条形图所示,请找出这些年龄的平均数、
众数、中位数,解释它们的含义.
人数
年龄
平均数:
=15(岁).
中位数:15岁.
众数:15岁.
该足球队平均年龄为15岁,处在中间位置的年龄也是15岁,15岁的人数也是最多的.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
中位数和众数
中位数:中间的一个数,或中间的两个数的平均数.
众数:出现次数最多的数.
平均数、中位数、众数的特征:平均数是最常用的指标,它表示“一般水平”,中位数表示“中等水平”,众数表示“多数水平”.
