21.2 一次函数的图像和性质 课件(2课时,共28张PPT) 2023-2024学年初中数学冀教版八年级下册
文档属性
| 名称 | 21.2 一次函数的图像和性质 课件(2课时,共28张PPT) 2023-2024学年初中数学冀教版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 327.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:00:20 | ||
图片预览




文档简介
(共28张PPT)
第二十一章 一次函数
21.2 一次函数的图像的性质
第1课时
1.会画一次函数的图像
2.知道一次函数y=kx+b与正比例函数y=kx的图像间的关系
典型例题
当堂检测
学习目标
课堂总结
在函数的表示中,我们学习了图像的表示形式和作图方法,那么一次函数的图像是怎么样的?以及如何绘制一次函数的图像呢?
典型例题
当堂检测
学习目标
课堂总结
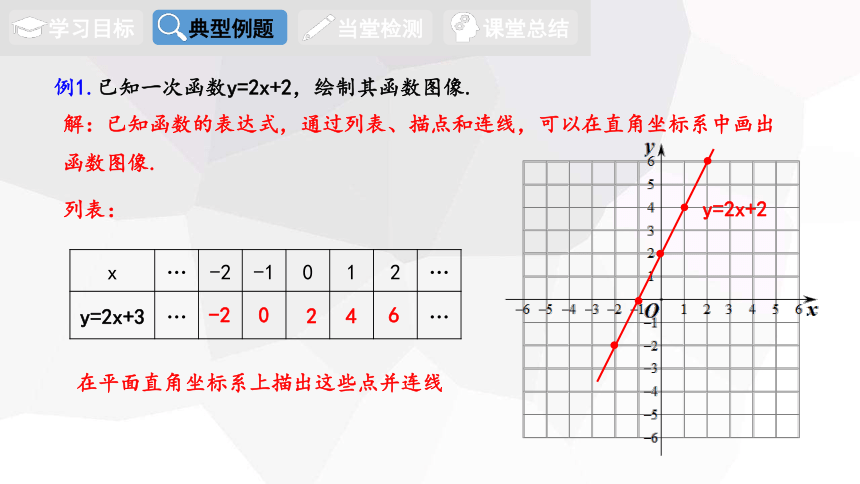
例1.已知一次函数y=2x+2,绘制其函数图像.
解:已知函数的表达式,通过列表、描点和连线,可以在直角坐标系中画出函数图像.
x … -2 -1 0 1 2 …
y=2x+3 … …
在平面直角坐标系上描出这些点并连线
2
4
y=2x+2
-2
0
6
列表:
典型例题
当堂检测
学习目标
课堂总结
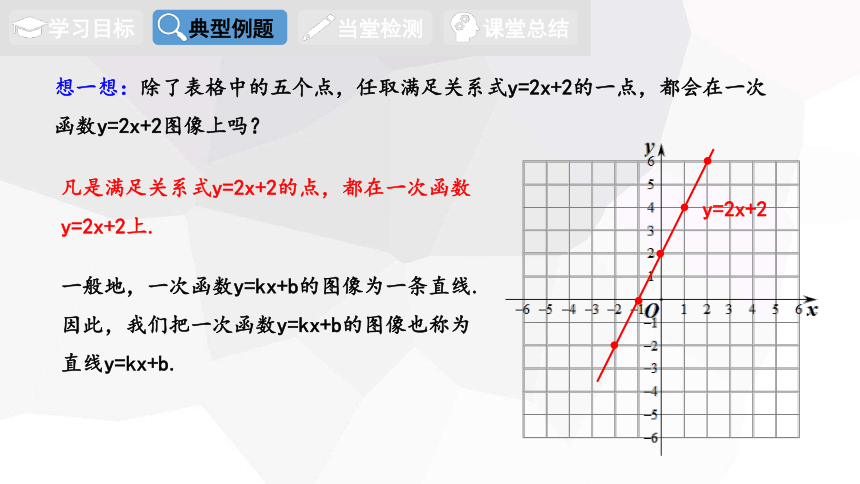
想一想:除了表格中的五个点,任取满足关系式y=2x+2的一点,都会在一次函数y=2x+2图像上吗?
凡是满足关系式y=2x+2的点,都在一次函数y=2x+2上.
y=2x+2
一般地,一次函数y=kx+b的图像为一条直线.因此,我们把一次函数y=kx+b的图像也称为直线y=kx+b.
典型例题
当堂检测
学习目标
课堂总结
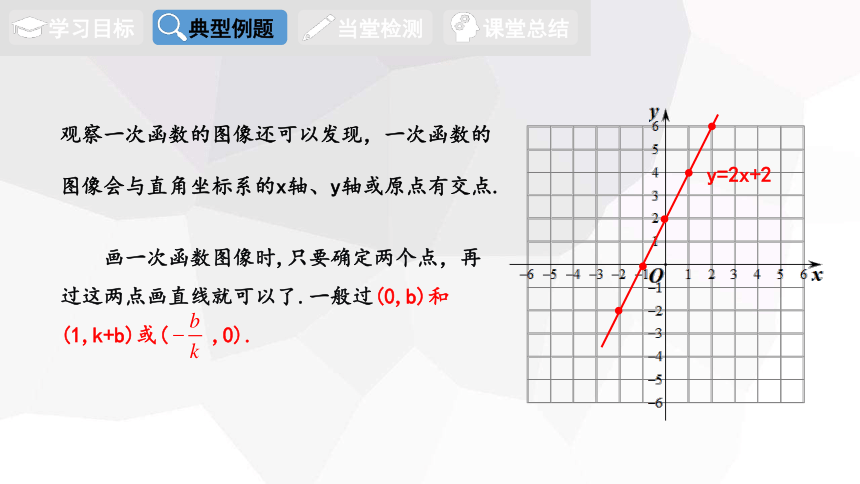
观察一次函数的图像还可以发现,一次函数的图像会与直角坐标系的x轴、y轴或原点有交点.
画一次函数图像时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或( ,0).
y=2x+2
典型例题
当堂检测
学习目标
课堂总结
一次函数的图象是一条直线,两点确定一条直线
1.小亮学习了一次函数的知识后,老师要求画y=2x-2的图像,他根据所学知识只描出了两个点(0,-2)和(1,0)很快就画出了y=2x-2的图像,那么小亮画图的依据是_______________________________________________.
解析:经过两点(0,b)和( ,0)或(1,k+b)可做直线y=kx+b.
学习目标
典型例题
当堂检测
课堂总结
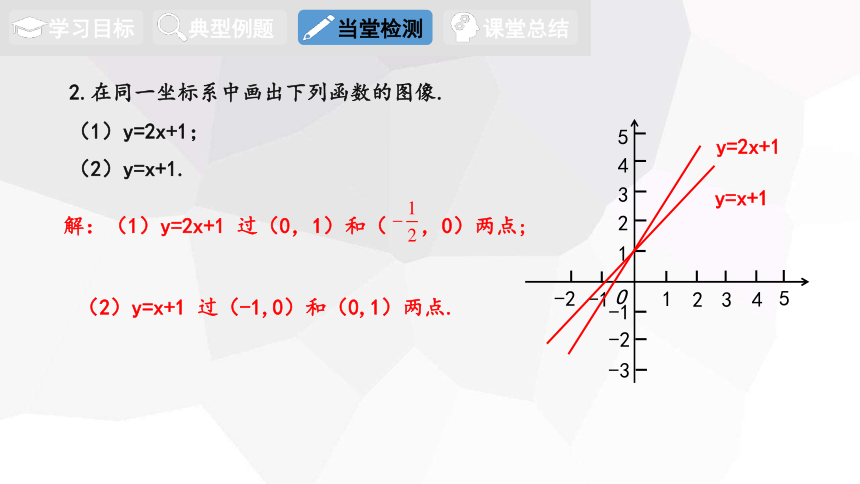
(2)y=x+1 过(-1,0)和(0,1)两点.
(2)y=x+1.
(1)y=2x+1;
2.在同一坐标系中画出下列函数的图像.
1
O
2
3
4
5
-2
-1
1
2
3
4
5
-1
-2
-3
解:(1)y=2x+1 过(0,1)和( ,0)两点;
y=2x+1
y=x+1
学习目标
典型例题
当堂检测
课堂总结
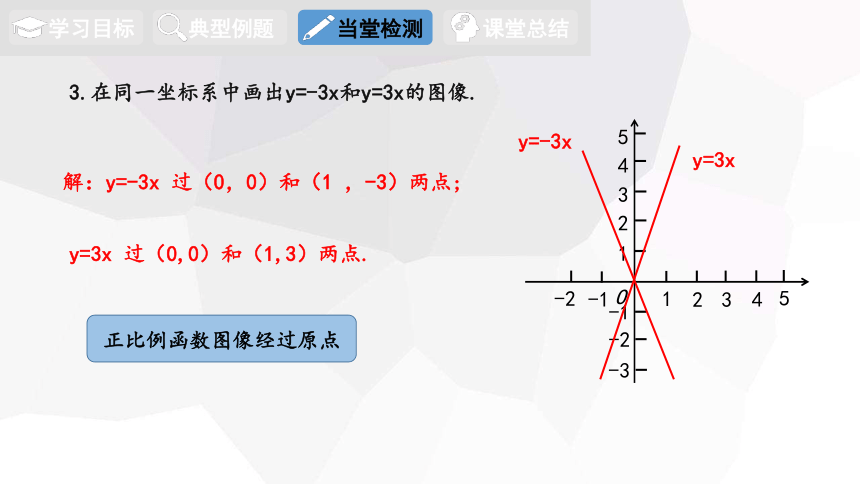
y=3x 过(0,0)和(1,3)两点.
3.在同一坐标系中画出y=-3x和y=3x的图像.
1
O
2
3
4
5
-2
-1
1
2
3
4
5
-1
-2
-3
解:y=-3x 过(0,0)和(1 ,-3)两点;
y=-3x
y=3x
正比例函数图像经过原点
学习目标
典型例题
当堂检测
课堂总结
例2.在同一个直角坐标系上画出下列函数的图像:
(1)y=-2x; (2)y=-2x+2.
解:(1)y=-2x的图像经过(0,0)和(1,-2)两点;
(2)y=-2x+2的图像经过(0,2)和(1,0)两点.
y=-2x+2
y=-2x
一次函数y=kx+b(k≠0)的图像可以由直线y=kx平移|b|个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).
典型例题
当堂检测
学习目标
课堂总结
4.若把直线y=9x向下平移5个单位长度,再向上平移3个单位长度,则得到的图像解析式是( )
A.y=9x+5 B.y=9x-5 C.y=9x-2 D.y=9x+8
C
解析:直线y=9x向下平移5个单位长度,得到:y=9x-5,
再向上平移3个单位长度,得到:y=9x-5+3=9x-2.
方法归纳:向上平移用加号,向下平移用减号.
学习目标
典型例题
当堂检测
课堂总结
一次函数y=kx+b(k≠0)的图像可以由直线y=kx平移|b|个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).
画一次函数图像时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或( ,0).
一般地,一次函数y=kx+b的图像为一条直线.因此,我们把一次函数y=kx+b的图像也称为直线y=kx+b.
学习目标
典型例题
当堂检测
课堂总结
第二十一章 一次函数
21.2 一次函数的图像的性质
第2课时
1.掌握一次函数的性质
2.能利用一次函数性质解决相关问题
典型例题
当堂检测
学习目标
课堂总结
概念剖析
知道一次函数的图像以及绘制方法后,你能从一次函数的图像中找到一次函数的性质吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.在同一直角坐标系中画出函数y=-2x+1和y=3x+2的图象,并说说它们分别经过的象限.
y=-2x+1
y=3x+2
解:过点(0,1)与点(1,-1)画出直线y=-2x+1;
过点(0,2)与点(1,5)画出直线y=3x+2.
观察图像可知,直线y=-2x+1经过一、二、四象限,
y的值随x的值增大而减小;
直线y=3x+2经过一、二、三象限,
y的值随x的值增大而增大.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
观察前面一次函数的图像,可以发现一次函数的性质:
对于一次函数y=kx+b(k,b为常数,且k≠0).
当k>0时,y 的值随x 的值的增大而增大;
当k<0时,y 的值随x 的值的增大而减小.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.在同一坐标系中画出函数 和y=5x-1的图象,并说说它们分别经过的象限.
过点(0,-1)与点(1,4)画出直线y=5x-1.
y=5x-1
直线 经过二、三、四象限;
直线y=5x-1经过一、三、四象限.
解:过点(0,-2)与点(1, )画出直线 ;
函数图像与y轴的交点位置与之前有何不同
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
当b>0时,点(0,b)在x轴上方;
当b<0时,点(0,b)在x轴下方;
当b=0时,点(0,0)是原点,即正比例函数y=kx(k≠0)为经过原点的一条直线.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.已知一次函数y=(1-2m)x+m+1,求当m为何值时,
(1)y随x的增大而增大
分析:当k>0时,y随x的增大而增大
解:∵y随x的增大而增大,
∴1-2m>0,
解得:m<
∴当m< 时,y随x的增大而增大.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.已知一次函数y=(1-2m)x+m+1,求当m为何值时,
(2)图象经过第一、二、四象限?
分析:当k<0,b>0时,图象经过第一、二、四象限
解:∵图象经过第一、二、四象限,
∴1-2m<0,m+1>0,
解得:m>
∴当m> 时,图象经过第一、二、四象限.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.已知一次函数y=(1-2m)x+m+1,求当m为何值时,
(3)图象与y轴的交点在x轴的上方
分析:当b>0时,与y轴交点在x轴上方,同时一次函数还要满足k不能为0.
解:∵图象与y轴的交点在x轴的上方,
∴m+1>0,
解得:m>-1,
∴当m>-1且m≠ 时,图象与y轴的交点在x轴的上方.
又∵1-2m≠0,
解得:m≠
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.(1)一次函数y=2x+3的图象经过第 象限,y随x的增大而 ,与y轴交点坐标为 .
(2)已知一次函数y=(m+2)x+1,函数y的值随x的值的增大而增大,则m的取值范围是 .
一、二、三
增大
(0,3)
m>-2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.判断下列函数中,y的值随x的增大而变化的情况.
解:-3<0,
∴y的值随x的增大而减小
解:(3-π)<0,
∴y的值随x的增大而减小
(1)y=-3x+3; (2)y=3x-3;
(3)y=(3-π)x; (4)y=0.5x;
解:3>0,
∴y的值随x的增大而增大
解:0.5>0,
∴y的值随x的增大而增大
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.已知一次函数y=(k+1)x-1,y的值随x的值增大而减小,求k的取值范围.
解:y的值随x的值增大而减小,
∴(k+1)<0
k<-1
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.已知,一次函数y=(1-3k)x+2k-1,试回答:
(1)k为何值时,y是x的正比例函数?
(2)当函数图象不经过第一象限时,求k的取值范围.
解:(1)∵y是x的正比例函数,
∴2k-1=0,
解得:
∴当 时,y是x的正比例函数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.已知,一次函数y=(1-3k)x+2k-1,试回答:
(2)当函数图象不经过第一象限时,求k的取值范围.
解:(2)当函数图象经过第二、四象限时,
当函数图象经过第二、三、四象限时,
解得:
∴当函数图象不经过第一象限时,k的取值范围为
综上:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
即:
一次函数y=kx+b(k,b为常数,且k≠0)的性质:
当k>0时,y 的值随x 的值的增大而增大;
当k<0时,y 的值随x 的值的增大而减小;
当b>0时,图像与y轴的交点(0,b)在x轴上方;
当b<0时,图像与y轴的交点(0,b)在x轴下方.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
第二十一章 一次函数
21.2 一次函数的图像的性质
第1课时
1.会画一次函数的图像
2.知道一次函数y=kx+b与正比例函数y=kx的图像间的关系
典型例题
当堂检测
学习目标
课堂总结
在函数的表示中,我们学习了图像的表示形式和作图方法,那么一次函数的图像是怎么样的?以及如何绘制一次函数的图像呢?
典型例题
当堂检测
学习目标
课堂总结
例1.已知一次函数y=2x+2,绘制其函数图像.
解:已知函数的表达式,通过列表、描点和连线,可以在直角坐标系中画出函数图像.
x … -2 -1 0 1 2 …
y=2x+3 … …
在平面直角坐标系上描出这些点并连线
2
4
y=2x+2
-2
0
6
列表:
典型例题
当堂检测
学习目标
课堂总结
想一想:除了表格中的五个点,任取满足关系式y=2x+2的一点,都会在一次函数y=2x+2图像上吗?
凡是满足关系式y=2x+2的点,都在一次函数y=2x+2上.
y=2x+2
一般地,一次函数y=kx+b的图像为一条直线.因此,我们把一次函数y=kx+b的图像也称为直线y=kx+b.
典型例题
当堂检测
学习目标
课堂总结
观察一次函数的图像还可以发现,一次函数的图像会与直角坐标系的x轴、y轴或原点有交点.
画一次函数图像时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或( ,0).
y=2x+2
典型例题
当堂检测
学习目标
课堂总结
一次函数的图象是一条直线,两点确定一条直线
1.小亮学习了一次函数的知识后,老师要求画y=2x-2的图像,他根据所学知识只描出了两个点(0,-2)和(1,0)很快就画出了y=2x-2的图像,那么小亮画图的依据是_______________________________________________.
解析:经过两点(0,b)和( ,0)或(1,k+b)可做直线y=kx+b.
学习目标
典型例题
当堂检测
课堂总结
(2)y=x+1 过(-1,0)和(0,1)两点.
(2)y=x+1.
(1)y=2x+1;
2.在同一坐标系中画出下列函数的图像.
1
O
2
3
4
5
-2
-1
1
2
3
4
5
-1
-2
-3
解:(1)y=2x+1 过(0,1)和( ,0)两点;
y=2x+1
y=x+1
学习目标
典型例题
当堂检测
课堂总结
y=3x 过(0,0)和(1,3)两点.
3.在同一坐标系中画出y=-3x和y=3x的图像.
1
O
2
3
4
5
-2
-1
1
2
3
4
5
-1
-2
-3
解:y=-3x 过(0,0)和(1 ,-3)两点;
y=-3x
y=3x
正比例函数图像经过原点
学习目标
典型例题
当堂检测
课堂总结
例2.在同一个直角坐标系上画出下列函数的图像:
(1)y=-2x; (2)y=-2x+2.
解:(1)y=-2x的图像经过(0,0)和(1,-2)两点;
(2)y=-2x+2的图像经过(0,2)和(1,0)两点.
y=-2x+2
y=-2x
一次函数y=kx+b(k≠0)的图像可以由直线y=kx平移|b|个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).
典型例题
当堂检测
学习目标
课堂总结
4.若把直线y=9x向下平移5个单位长度,再向上平移3个单位长度,则得到的图像解析式是( )
A.y=9x+5 B.y=9x-5 C.y=9x-2 D.y=9x+8
C
解析:直线y=9x向下平移5个单位长度,得到:y=9x-5,
再向上平移3个单位长度,得到:y=9x-5+3=9x-2.
方法归纳:向上平移用加号,向下平移用减号.
学习目标
典型例题
当堂检测
课堂总结
一次函数y=kx+b(k≠0)的图像可以由直线y=kx平移|b|个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).
画一次函数图像时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或( ,0).
一般地,一次函数y=kx+b的图像为一条直线.因此,我们把一次函数y=kx+b的图像也称为直线y=kx+b.
学习目标
典型例题
当堂检测
课堂总结
第二十一章 一次函数
21.2 一次函数的图像的性质
第2课时
1.掌握一次函数的性质
2.能利用一次函数性质解决相关问题
典型例题
当堂检测
学习目标
课堂总结
概念剖析
知道一次函数的图像以及绘制方法后,你能从一次函数的图像中找到一次函数的性质吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.在同一直角坐标系中画出函数y=-2x+1和y=3x+2的图象,并说说它们分别经过的象限.
y=-2x+1
y=3x+2
解:过点(0,1)与点(1,-1)画出直线y=-2x+1;
过点(0,2)与点(1,5)画出直线y=3x+2.
观察图像可知,直线y=-2x+1经过一、二、四象限,
y的值随x的值增大而减小;
直线y=3x+2经过一、二、三象限,
y的值随x的值增大而增大.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
观察前面一次函数的图像,可以发现一次函数的性质:
对于一次函数y=kx+b(k,b为常数,且k≠0).
当k>0时,y 的值随x 的值的增大而增大;
当k<0时,y 的值随x 的值的增大而减小.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.在同一坐标系中画出函数 和y=5x-1的图象,并说说它们分别经过的象限.
过点(0,-1)与点(1,4)画出直线y=5x-1.
y=5x-1
直线 经过二、三、四象限;
直线y=5x-1经过一、三、四象限.
解:过点(0,-2)与点(1, )画出直线 ;
函数图像与y轴的交点位置与之前有何不同
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
当b>0时,点(0,b)在x轴上方;
当b<0时,点(0,b)在x轴下方;
当b=0时,点(0,0)是原点,即正比例函数y=kx(k≠0)为经过原点的一条直线.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.已知一次函数y=(1-2m)x+m+1,求当m为何值时,
(1)y随x的增大而增大
分析:当k>0时,y随x的增大而增大
解:∵y随x的增大而增大,
∴1-2m>0,
解得:m<
∴当m< 时,y随x的增大而增大.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.已知一次函数y=(1-2m)x+m+1,求当m为何值时,
(2)图象经过第一、二、四象限?
分析:当k<0,b>0时,图象经过第一、二、四象限
解:∵图象经过第一、二、四象限,
∴1-2m<0,m+1>0,
解得:m>
∴当m> 时,图象经过第一、二、四象限.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.已知一次函数y=(1-2m)x+m+1,求当m为何值时,
(3)图象与y轴的交点在x轴的上方
分析:当b>0时,与y轴交点在x轴上方,同时一次函数还要满足k不能为0.
解:∵图象与y轴的交点在x轴的上方,
∴m+1>0,
解得:m>-1,
∴当m>-1且m≠ 时,图象与y轴的交点在x轴的上方.
又∵1-2m≠0,
解得:m≠
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.(1)一次函数y=2x+3的图象经过第 象限,y随x的增大而 ,与y轴交点坐标为 .
(2)已知一次函数y=(m+2)x+1,函数y的值随x的值的增大而增大,则m的取值范围是 .
一、二、三
增大
(0,3)
m>-2
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.判断下列函数中,y的值随x的增大而变化的情况.
解:-3<0,
∴y的值随x的增大而减小
解:(3-π)<0,
∴y的值随x的增大而减小
(1)y=-3x+3; (2)y=3x-3;
(3)y=(3-π)x; (4)y=0.5x;
解:3>0,
∴y的值随x的增大而增大
解:0.5>0,
∴y的值随x的增大而增大
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.已知一次函数y=(k+1)x-1,y的值随x的值增大而减小,求k的取值范围.
解:y的值随x的值增大而减小,
∴(k+1)<0
k<-1
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.已知,一次函数y=(1-3k)x+2k-1,试回答:
(1)k为何值时,y是x的正比例函数?
(2)当函数图象不经过第一象限时,求k的取值范围.
解:(1)∵y是x的正比例函数,
∴2k-1=0,
解得:
∴当 时,y是x的正比例函数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.已知,一次函数y=(1-3k)x+2k-1,试回答:
(2)当函数图象不经过第一象限时,求k的取值范围.
解:(2)当函数图象经过第二、四象限时,
当函数图象经过第二、三、四象限时,
解得:
∴当函数图象不经过第一象限时,k的取值范围为
综上:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
即:
一次函数y=kx+b(k,b为常数,且k≠0)的性质:
当k>0时,y 的值随x 的值的增大而增大;
当k<0时,y 的值随x 的值的增大而减小;
当b>0时,图像与y轴的交点(0,b)在x轴上方;
当b<0时,图像与y轴的交点(0,b)在x轴下方.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
