21.4 一次函数的应用 第2课时 课件(共16张PPT) 2023-2024学年初中数学冀教版八年级下册
文档属性
| 名称 | 21.4 一次函数的应用 第2课时 课件(共16张PPT) 2023-2024学年初中数学冀教版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 206.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:02:40 | ||
图片预览






文档简介
(共16张PPT)
第二十一章 一次函数
21.4 一次函数的应用
第2课时
1.能够利用两条直线解决简单的实际问题.
2.通过两个函数图像获取相应的信息,进一步增强图识能力,加强数形结合意识.
典型例题
当堂检测
学习目标
课堂总结
某学校准备组织师生去长白山游玩,甲、乙两家旅行社原价都是每人60元,且都表示对学生优惠,甲旅行社表示:全部8折收费,乙旅行社表示:若人数不超过30人,则按9折收费;若超过30人,则超过部分按7折收费,其余按9折收费.如果你是一位老师,你觉得选择哪家旅行社更优惠呢?你能用图像说明你发现的问题吗?
典型例题
当堂检测
学习目标
课堂总结
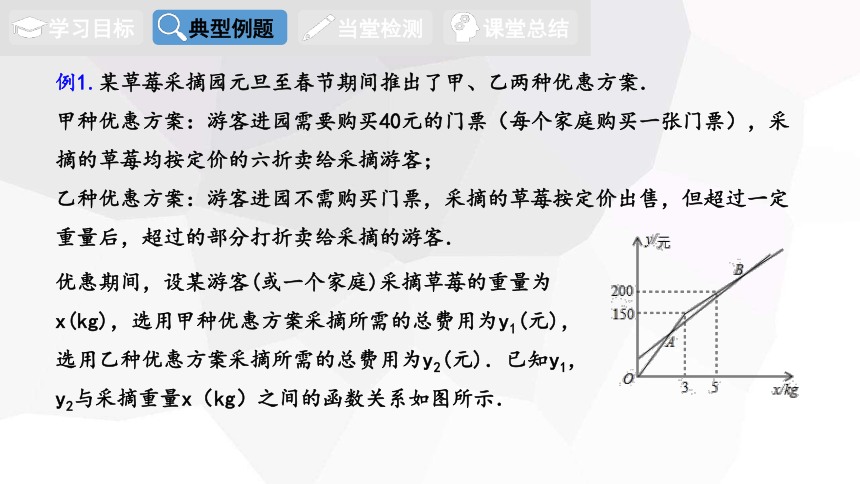
例1.某草莓采摘园元旦至春节期间推出了甲、乙两种优惠方案.
甲种优惠方案:游客进园需要购买40元的门票(每个家庭购买一张门票),采摘的草莓均按定价的六折卖给采摘游客;
乙种优惠方案:游客进园不需购买门票,采摘的草莓按定价出售,但超过一定重量后,超过的部分打折卖给采摘的游客.
优惠期间,设某游客(或一个家庭)采摘草莓的重量为x(kg),选用甲种优惠方案采摘所需的总费用为y1(元),选用乙种优惠方案采摘所需的总费用为y2(元).已知y1,y2与采摘重量x(kg)之间的函数关系如图所示.
典型例题
当堂检测
学习目标
课堂总结
(1)分别求y1,y2与x之间的函数关系式;
解:采摘园优惠前的草莓定价为 (元/kg)
由题意,得y1=50×0.6x+40=30x+40.
当0≤x≤3时,设y2=kx,根据题意,得150=3k.解得k=50.
∵y2=50x;
当x>3时,设y2=kx+b,由题意知y2=kx+b的图像过点将(3,150)和(5,200),
解得 ,
∴y2=25x+75.
则 ,
典型例题
当堂检测
学习目标
课堂总结
(2)求点A的坐标,并解释坐标的实际意义;
25x+75=30x+40,
解得x=7,
从图像中可以看出,当采摘重量为2<x<7时,游客选用甲种方案更合算.
解得 则点A的坐标为(2,100)
实际意义是当采摘重量为2kg时,两种优惠方案的总费用都为100元.
根据题意,得 ,
(3)采摘重量x为多少时,游客选用甲种优惠方案采摘更合算.
典型例题
当堂检测
学习目标
课堂总结
2.根据图像或者方程,求出自变量在取何值时所对应的函数值相等,给出一个自变量大小,判断对应函数值大小选择方案.
总结:
利用一次函数进行方案决策
1.从数学的角度分析数学问题,建立函数模型;
结合实际需要,选择最佳方案.
典型例题
当堂检测
学习目标
课堂总结
解析:由图可知,通话时间为500分钟时,方案A的费用是230元,方案B的费用是168元,∵230>168,∴选择方案B更优惠.
1.电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )
A. 方案A B. 方案B
C. 两种方案一样优惠 D. 不能确定
B
学习目标
典型例题
当堂检测
课堂总结
2.某工厂开发生产一种新产品,前期投入150000元,生产时,每件成本为25元,每件销售价为40元,设生产x件时,总成本(包括前期投入)为y1元,销售额为y2元.
(1)分别求出y1,y2与x之间的函数关系式.
解:(1)y1=15000+25x
y2=40x
学习目标
典型例题
当堂检测
课堂总结
2.某工厂开发生产一种新产品,前期投入150000元,生产时,每件成本为25元,每件销售价为40元,设生产x件时,总成本(包括前期投入)为y1元,销售额为y2元.
(2)至少生产并销售多少件产品后,工厂才会有盈利?
解:(2)15000+25x=40x
解得 x=1000
画出函数图像:
y/元
15000
O
x/件
30000
40000
1000
答:至少生产并销售1000件产品后,工厂才会有盈利.
学习目标
典型例题
当堂检测
课堂总结
y2
y1
3.某工厂有甲、乙两个净化水池,容积都是480 m3.注满乙池的水得到净化可以使用时,甲池未净化的水已有192 m3.此时,乙池以10 m3/h的速度将水放出使用,而甲池仍以8 m3/h的速度注水.设乙池放水为x h时,甲、乙两池中的水量用y m3表示.
乙池:y=480-10x(0≤x≤48).
解:(1)甲池:y=192+8x(0≤x≤36);
(1)分别写出甲、乙两池中的水量y关于x的函数关系式及自变量x的取值范围,并在同一直角坐标系中画出这两个函数的图像.
y/m3
200
O
x/h
480
20
30
40
48
192
400
10
36
学习目标
典型例题
当堂检测
课堂总结
y乙=480-10x
y甲=192+8x
(2)借助由(1)得出的图像回答:
①x取何值时,甲、乙两池水量相等?
②x取哪些值时,甲池的水量少于乙池的水量?
③x取哪些值时,甲池的水量多于乙池的水量?
解得:x=16,
① 192+8x=480-10x,
y/m3
200
O
x/h
480
20
30
40
48
192
400
10
36
x=16时,甲、乙两池水量相等;
② x<16时,甲池的水量小于乙池的水量;
③ x>16时,甲池的水量多于乙池的水量.
学习目标
典型例题
当堂检测
课堂总结
y乙=480-10x
y甲=192+8x
4.甲、乙两车同时从A城出发驶向B城.甲车到达B城后立即返回.如图它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图像
(1)求甲车行驶过程中y与x的函数表达式.并写出自变量x的取值范围;
解:(1)设甲车行驶过程中y与x之间的函数表达式为y甲=k1x+b1,
当0≤x≤6时,将点(0,0),(6,600)代入函数表达式得:
解得
∴y甲=100x;
学习目标
典型例题
当堂检测
课堂总结
(1)求甲车行驶过程中y与x的函数表达式.并写出自变量x的取值范围;
当6<x≤14,将点(6,600),(14,0)代入函数表达式得:
解得
∴y甲=-75x+1050;
综上得:y甲=
学习目标
典型例题
当堂检测
课堂总结
(2)求相遇时间和乙车速度;
(3)在什么时间段内甲车在乙车前面?
(2)当x=7时,两车相遇,此时y甲=-75×7+1050=525,
乙车的速度为:525÷7=75(千米/小时).
(3)在出发7小时前,甲车在乙车前面.
学习目标
典型例题
当堂检测
课堂总结
1.建立适当的函数模型是解题的基础.
2.根据图像或者方程,求出自变量在取何值时所对应的函数值相等,给出一个自变量大小,判断对应函数值大小选择方案.
3.解决实际问题时,要进行综合实际情况比较.
学习目标
典型例题
当堂检测
课堂总结
第二十一章 一次函数
21.4 一次函数的应用
第2课时
1.能够利用两条直线解决简单的实际问题.
2.通过两个函数图像获取相应的信息,进一步增强图识能力,加强数形结合意识.
典型例题
当堂检测
学习目标
课堂总结
某学校准备组织师生去长白山游玩,甲、乙两家旅行社原价都是每人60元,且都表示对学生优惠,甲旅行社表示:全部8折收费,乙旅行社表示:若人数不超过30人,则按9折收费;若超过30人,则超过部分按7折收费,其余按9折收费.如果你是一位老师,你觉得选择哪家旅行社更优惠呢?你能用图像说明你发现的问题吗?
典型例题
当堂检测
学习目标
课堂总结
例1.某草莓采摘园元旦至春节期间推出了甲、乙两种优惠方案.
甲种优惠方案:游客进园需要购买40元的门票(每个家庭购买一张门票),采摘的草莓均按定价的六折卖给采摘游客;
乙种优惠方案:游客进园不需购买门票,采摘的草莓按定价出售,但超过一定重量后,超过的部分打折卖给采摘的游客.
优惠期间,设某游客(或一个家庭)采摘草莓的重量为x(kg),选用甲种优惠方案采摘所需的总费用为y1(元),选用乙种优惠方案采摘所需的总费用为y2(元).已知y1,y2与采摘重量x(kg)之间的函数关系如图所示.
典型例题
当堂检测
学习目标
课堂总结
(1)分别求y1,y2与x之间的函数关系式;
解:采摘园优惠前的草莓定价为 (元/kg)
由题意,得y1=50×0.6x+40=30x+40.
当0≤x≤3时,设y2=kx,根据题意,得150=3k.解得k=50.
∵y2=50x;
当x>3时,设y2=kx+b,由题意知y2=kx+b的图像过点将(3,150)和(5,200),
解得 ,
∴y2=25x+75.
则 ,
典型例题
当堂检测
学习目标
课堂总结
(2)求点A的坐标,并解释坐标的实际意义;
25x+75=30x+40,
解得x=7,
从图像中可以看出,当采摘重量为2<x<7时,游客选用甲种方案更合算.
解得 则点A的坐标为(2,100)
实际意义是当采摘重量为2kg时,两种优惠方案的总费用都为100元.
根据题意,得 ,
(3)采摘重量x为多少时,游客选用甲种优惠方案采摘更合算.
典型例题
当堂检测
学习目标
课堂总结
2.根据图像或者方程,求出自变量在取何值时所对应的函数值相等,给出一个自变量大小,判断对应函数值大小选择方案.
总结:
利用一次函数进行方案决策
1.从数学的角度分析数学问题,建立函数模型;
结合实际需要,选择最佳方案.
典型例题
当堂检测
学习目标
课堂总结
解析:由图可知,通话时间为500分钟时,方案A的费用是230元,方案B的费用是168元,∵230>168,∴选择方案B更优惠.
1.电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )
A. 方案A B. 方案B
C. 两种方案一样优惠 D. 不能确定
B
学习目标
典型例题
当堂检测
课堂总结
2.某工厂开发生产一种新产品,前期投入150000元,生产时,每件成本为25元,每件销售价为40元,设生产x件时,总成本(包括前期投入)为y1元,销售额为y2元.
(1)分别求出y1,y2与x之间的函数关系式.
解:(1)y1=15000+25x
y2=40x
学习目标
典型例题
当堂检测
课堂总结
2.某工厂开发生产一种新产品,前期投入150000元,生产时,每件成本为25元,每件销售价为40元,设生产x件时,总成本(包括前期投入)为y1元,销售额为y2元.
(2)至少生产并销售多少件产品后,工厂才会有盈利?
解:(2)15000+25x=40x
解得 x=1000
画出函数图像:
y/元
15000
O
x/件
30000
40000
1000
答:至少生产并销售1000件产品后,工厂才会有盈利.
学习目标
典型例题
当堂检测
课堂总结
y2
y1
3.某工厂有甲、乙两个净化水池,容积都是480 m3.注满乙池的水得到净化可以使用时,甲池未净化的水已有192 m3.此时,乙池以10 m3/h的速度将水放出使用,而甲池仍以8 m3/h的速度注水.设乙池放水为x h时,甲、乙两池中的水量用y m3表示.
乙池:y=480-10x(0≤x≤48).
解:(1)甲池:y=192+8x(0≤x≤36);
(1)分别写出甲、乙两池中的水量y关于x的函数关系式及自变量x的取值范围,并在同一直角坐标系中画出这两个函数的图像.
y/m3
200
O
x/h
480
20
30
40
48
192
400
10
36
学习目标
典型例题
当堂检测
课堂总结
y乙=480-10x
y甲=192+8x
(2)借助由(1)得出的图像回答:
①x取何值时,甲、乙两池水量相等?
②x取哪些值时,甲池的水量少于乙池的水量?
③x取哪些值时,甲池的水量多于乙池的水量?
解得:x=16,
① 192+8x=480-10x,
y/m3
200
O
x/h
480
20
30
40
48
192
400
10
36
x=16时,甲、乙两池水量相等;
② x<16时,甲池的水量小于乙池的水量;
③ x>16时,甲池的水量多于乙池的水量.
学习目标
典型例题
当堂检测
课堂总结
y乙=480-10x
y甲=192+8x
4.甲、乙两车同时从A城出发驶向B城.甲车到达B城后立即返回.如图它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图像
(1)求甲车行驶过程中y与x的函数表达式.并写出自变量x的取值范围;
解:(1)设甲车行驶过程中y与x之间的函数表达式为y甲=k1x+b1,
当0≤x≤6时,将点(0,0),(6,600)代入函数表达式得:
解得
∴y甲=100x;
学习目标
典型例题
当堂检测
课堂总结
(1)求甲车行驶过程中y与x的函数表达式.并写出自变量x的取值范围;
当6<x≤14,将点(6,600),(14,0)代入函数表达式得:
解得
∴y甲=-75x+1050;
综上得:y甲=
学习目标
典型例题
当堂检测
课堂总结
(2)求相遇时间和乙车速度;
(3)在什么时间段内甲车在乙车前面?
(2)当x=7时,两车相遇,此时y甲=-75×7+1050=525,
乙车的速度为:525÷7=75(千米/小时).
(3)在出发7小时前,甲车在乙车前面.
学习目标
典型例题
当堂检测
课堂总结
1.建立适当的函数模型是解题的基础.
2.根据图像或者方程,求出自变量在取何值时所对应的函数值相等,给出一个自变量大小,判断对应函数值大小选择方案.
3.解决实际问题时,要进行综合实际情况比较.
学习目标
典型例题
当堂检测
课堂总结
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
