22.2 平行四边形的判定课件 (第1-2课时) 28张PPT 2023-2024学年初中数学冀教版八年级下册
文档属性
| 名称 | 22.2 平行四边形的判定课件 (第1-2课时) 28张PPT 2023-2024学年初中数学冀教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 842.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 09:32:27 | ||
图片预览




文档简介
(共28张PPT)
第1课时
第二十二章 四边形
22.2 平行四边形的判定
1.掌握平行四边形的判定定理1
2.会运用平行四边形的定义及判定定理判别一个四边形
是否为平行四边形
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考:我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
想一想:具备什么条件的四边形是平行四边形?
文字语言:两组对边分别平行的四边形叫做平行四边形.
几何语言:如图,∵ AB∥CD,AD∥BC ,
∴ 四边形ABCD是平行四边形.
定义法:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
A
B
C
D
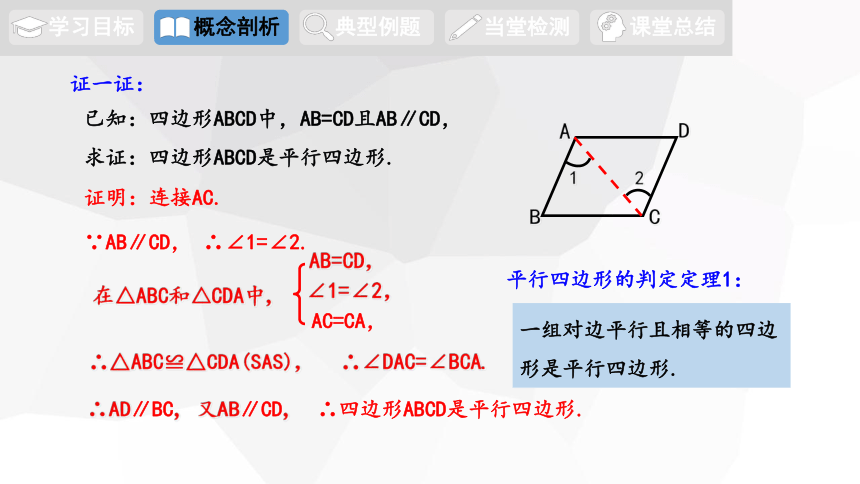
证一证:
已知:四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
∴∠DAC=∠BCA.
∴四边形ABCD是平行四边形.
∴AD∥BC,
A
B
C
D
2
1
AB=CD,
AC=CA,
∠1=∠2,
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
又AB∥CD,
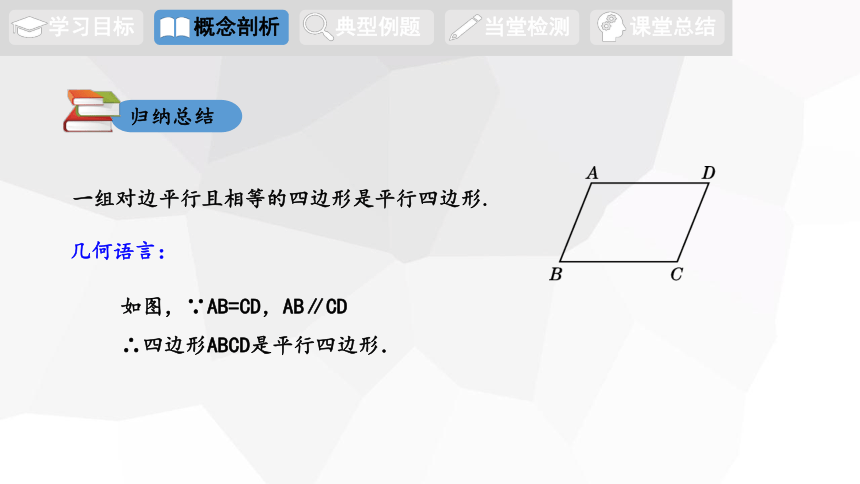
一组对边平行且相等的四边形是平行四边形.
如图,∵AB=CD,AB∥CD
∴四边形ABCD是平行四边形.
几何语言:
归纳总结
典型例题
当堂检测
学习目标
课堂总结
概念剖析
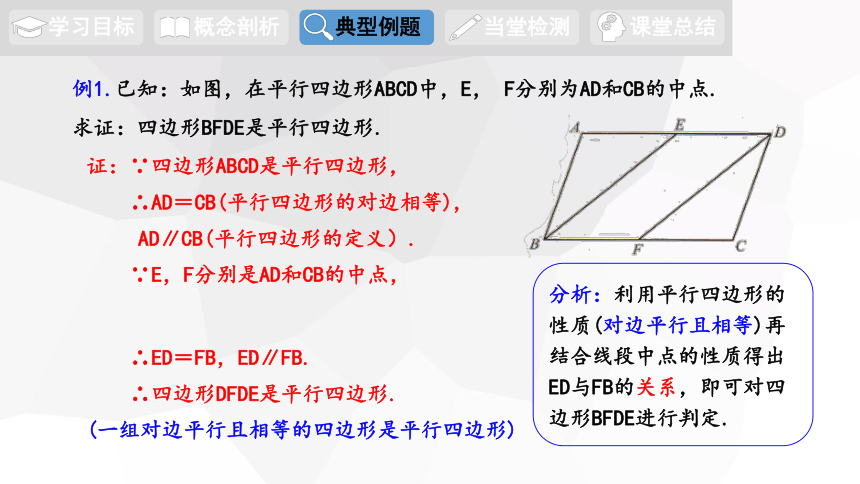
例1.已知:如图,在平行四边形ABCD中,E, F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
分析:利用平行四边形的性质(对边平行且相等)再结合线段中点的性质得出ED与FB的关系,即可对四边形BFDE进行判定.
证:∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED=FB,ED∥FB.
∴四边形DFDE是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
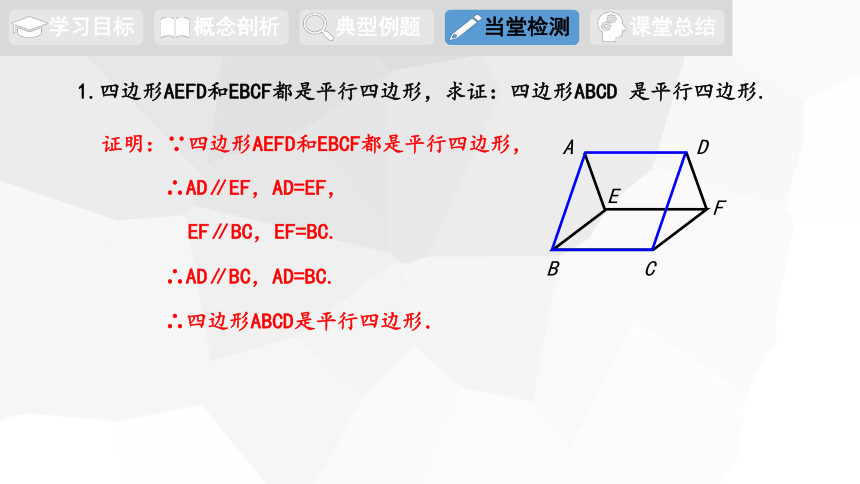
1.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥EF,AD=EF,
EF∥BC,EF=BC.
∴AD∥BC,AD=BC.
∴四边形ABCD是平行四边形.
A
B
C
D
E
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.两组对角相等的四边形是平行四边形吗?为什么?
证明:设在四边形ABCD中,∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
又∵∠A=∠C,∠B=∠D.
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴ AD∥BC.
同理得 AB∥CD,
∴四边形ABCD是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,在四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
证明:∵AE⊥AD,CF⊥BC,
∵AD∥BC,
∴∠ADE=∠CBF,
在Rt△AED和Rt△CFB中,
∴Rt△AED≌Rt△CFB(AAS).
∴AD=BC,
∴四边形ABCD是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,在平行四边形ABCD中,点M、N分别是AD、BC上的两点,点E、F
在对角线BD上,且DM=BN,BE=DF. 求证:四边形MENF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥CB,
∵DM=BN ,DF=BE
∴△MDF≌△NBE
∴MF=EN,∠MFD=∠NEB
∴∠MFE=∠NEF,
∴四边形MENF是平行四边形.
∴∠MDF=∠NBE
∴MF∥EN
典型例题
当堂检测
学习目标
课堂总结
概念剖析
平行四边形的判定方法
一组对边平行且相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
第2课时
第二十二章 四边形
22.2 平行四边形的判定
1.能运用两组对边分别相等判定一个四边形为平行四边形
2.能运用对角线互相平分判定一个四边形为平行四边形
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考:
如图,一个木匠,将两根木条AC,BD的中点重叠,并用钉子固定就得到了
一个平行四边形ABCD,木匠的做法有什么依据吗?
依据:平行四边形的对角线互相平分.
对角线互相平分的四边形是平行四边形吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
已知:四边形ABCD中,OA=OC,OB=OD. 求证:四边形ABCD是平行四边形.
A
B
C
D
证明:在△AOB和△COD中,
∴△AOB≌△COD(SAS),
∴∠BAO=∠OCD ,AB=DC,
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
对角线互相平分的四边形是平行四边形.
O
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
平行四边形对边相等,如果四边形两组对边分别相等是平行四边形吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
∴AB∥DC,
已知:四边形ABCD中,AB=DC,AD=BC.求证:四边形ABCD是平行四边形.
A
B
C
D
证明:连接AC,
1
4
2
3
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS)
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴ ∠1=∠4 , ∠2=∠3,
∴AB∥CD , AD∥BC,
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
两条对角线互相平分的四边形是平行四边形.
几何语言:
如图,∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
证明:在平行四边形ABCD中,
∠A=∠C,AD=BC,
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.
(两组对边分别相等的四边形是平行四边形)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
方法总结:在判定平行四边形时,要根据题意灵活选择判定方法,有时
要注意结合平行四边形的性质和判定三角形全等的方法,先得出边、角
关系,再进行判定.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,在Rt△MON中,∠MON=90°.求证:四边形PONM是平行四边形.
证明:Rt△MON中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.如图,□ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
(对角线互相平分的四边形的平行四边形)
B
O
D
A
C
E
F
分析:首先利用平行四边形的性质,得出对角线互相平分,进而得出EO=FO,BO=DO,即可对四边形BFDE进行判定.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
D
A.6 B.12
C.20 D.24
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
求证:四边形ABCD是平行四边形.
证明:∵O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠ADO=∠CBO,
在△AOD和△COB中,
∴△AOD≌△COB(AAS),
∴OD=OB,
∴四边形ABCD是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别是
OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由.
解:四边形BFDE是平行四边形,
理由:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.
又∵E,F分别是OA和OC的中点,
∴OE=OF.
∴四边形BFDE是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
6.已知:如图,□ABCD的对角线AC,BD交于点0,EF过点0交AD于点E,交BC于点F,点G是OA的中点,点H是OC的中点.求证:四边形EGFH是平行四边形.
证明:∵AC是□ABCD的对角线,EF过点0交AD于点E,
∴∠EAO=∠FCO,
∴∠AOE=∠FOC,AO=OC,AD∥BC
∴△AOE≌△FOC,
∵点G、H分别是OA、OC的中点,
∴AG=GO=OH=HC,
∴四边形EGFH是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
∴EO=OF,
平行四边形的判定方法:
1.两组对边分别相等的四边形是平行四边形.
2.两条对角线互相平分的四边形是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
第1课时
第二十二章 四边形
22.2 平行四边形的判定
1.掌握平行四边形的判定定理1
2.会运用平行四边形的定义及判定定理判别一个四边形
是否为平行四边形
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考:我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
想一想:具备什么条件的四边形是平行四边形?
文字语言:两组对边分别平行的四边形叫做平行四边形.
几何语言:如图,∵ AB∥CD,AD∥BC ,
∴ 四边形ABCD是平行四边形.
定义法:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
A
B
C
D
证一证:
已知:四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
∴∠DAC=∠BCA.
∴四边形ABCD是平行四边形.
∴AD∥BC,
A
B
C
D
2
1
AB=CD,
AC=CA,
∠1=∠2,
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
又AB∥CD,
一组对边平行且相等的四边形是平行四边形.
如图,∵AB=CD,AB∥CD
∴四边形ABCD是平行四边形.
几何语言:
归纳总结
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.已知:如图,在平行四边形ABCD中,E, F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
分析:利用平行四边形的性质(对边平行且相等)再结合线段中点的性质得出ED与FB的关系,即可对四边形BFDE进行判定.
证:∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED=FB,ED∥FB.
∴四边形DFDE是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥EF,AD=EF,
EF∥BC,EF=BC.
∴AD∥BC,AD=BC.
∴四边形ABCD是平行四边形.
A
B
C
D
E
F
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.两组对角相等的四边形是平行四边形吗?为什么?
证明:设在四边形ABCD中,∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
又∵∠A=∠C,∠B=∠D.
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴ AD∥BC.
同理得 AB∥CD,
∴四边形ABCD是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,在四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
证明:∵AE⊥AD,CF⊥BC,
∵AD∥BC,
∴∠ADE=∠CBF,
在Rt△AED和Rt△CFB中,
∴Rt△AED≌Rt△CFB(AAS).
∴AD=BC,
∴四边形ABCD是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,在平行四边形ABCD中,点M、N分别是AD、BC上的两点,点E、F
在对角线BD上,且DM=BN,BE=DF. 求证:四边形MENF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥CB,
∵DM=BN ,DF=BE
∴△MDF≌△NBE
∴MF=EN,∠MFD=∠NEB
∴∠MFE=∠NEF,
∴四边形MENF是平行四边形.
∴∠MDF=∠NBE
∴MF∥EN
典型例题
当堂检测
学习目标
课堂总结
概念剖析
平行四边形的判定方法
一组对边平行且相等的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
第2课时
第二十二章 四边形
22.2 平行四边形的判定
1.能运用两组对边分别相等判定一个四边形为平行四边形
2.能运用对角线互相平分判定一个四边形为平行四边形
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考:
如图,一个木匠,将两根木条AC,BD的中点重叠,并用钉子固定就得到了
一个平行四边形ABCD,木匠的做法有什么依据吗?
依据:平行四边形的对角线互相平分.
对角线互相平分的四边形是平行四边形吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
已知:四边形ABCD中,OA=OC,OB=OD. 求证:四边形ABCD是平行四边形.
A
B
C
D
证明:在△AOB和△COD中,
∴△AOB≌△COD(SAS),
∴∠BAO=∠OCD ,AB=DC,
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
对角线互相平分的四边形是平行四边形.
O
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
平行四边形对边相等,如果四边形两组对边分别相等是平行四边形吗?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
∴AB∥DC,
已知:四边形ABCD中,AB=DC,AD=BC.求证:四边形ABCD是平行四边形.
A
B
C
D
证明:连接AC,
1
4
2
3
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS)
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴ ∠1=∠4 , ∠2=∠3,
∴AB∥CD , AD∥BC,
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
两条对角线互相平分的四边形是平行四边形.
几何语言:
如图,∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
证明:在平行四边形ABCD中,
∠A=∠C,AD=BC,
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.
(两组对边分别相等的四边形是平行四边形)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
方法总结:在判定平行四边形时,要根据题意灵活选择判定方法,有时
要注意结合平行四边形的性质和判定三角形全等的方法,先得出边、角
关系,再进行判定.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.如图,在Rt△MON中,∠MON=90°.求证:四边形PONM是平行四边形.
证明:Rt△MON中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.如图,□ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
(对角线互相平分的四边形的平行四边形)
B
O
D
A
C
E
F
分析:首先利用平行四边形的性质,得出对角线互相平分,进而得出EO=FO,BO=DO,即可对四边形BFDE进行判定.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
D
A.6 B.12
C.20 D.24
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
求证:四边形ABCD是平行四边形.
证明:∵O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠ADO=∠CBO,
在△AOD和△COB中,
∴△AOD≌△COB(AAS),
∴OD=OB,
∴四边形ABCD是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别是
OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由.
解:四边形BFDE是平行四边形,
理由:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.
又∵E,F分别是OA和OC的中点,
∴OE=OF.
∴四边形BFDE是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
6.已知:如图,□ABCD的对角线AC,BD交于点0,EF过点0交AD于点E,交BC于点F,点G是OA的中点,点H是OC的中点.求证:四边形EGFH是平行四边形.
证明:∵AC是□ABCD的对角线,EF过点0交AD于点E,
∴∠EAO=∠FCO,
∴∠AOE=∠FOC,AO=OC,AD∥BC
∴△AOE≌△FOC,
∵点G、H分别是OA、OC的中点,
∴AG=GO=OH=HC,
∴四边形EGFH是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
∴EO=OF,
平行四边形的判定方法:
1.两组对边分别相等的四边形是平行四边形.
2.两条对角线互相平分的四边形是平行四边形.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
