第二十一章 一次函数 复习课 课件(共30张PPT) 2023-2024学年初中数学冀教版八年级下册
文档属性
| 名称 | 第二十一章 一次函数 复习课 课件(共30张PPT) 2023-2024学年初中数学冀教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 470.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
复习课
第二十一章 一次函数
1.通过函数图像理解一次函数的性质
2.会用待定系数法求一次函数的表达式
3.知道一次函数与二元一次方程(组)之间的联系,并能解决相关问题
典型例题
当堂检测
学习目标
课堂总结
知识梳理
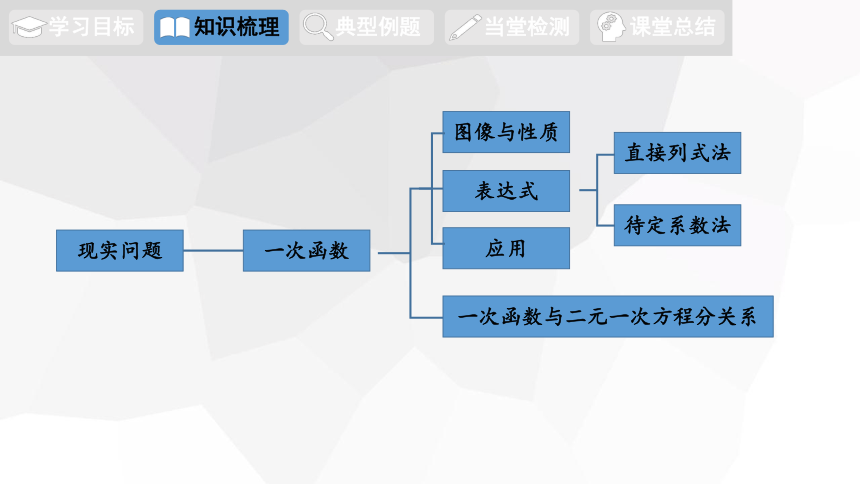
现实问题
一次函数
图像与性质
表达式
应用
一次函数与二元一次方程分关系
直接列式法
待定系数法
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.正比例函数:
(1)定义:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
(2)图像与性质:
一般地,正比例函数y=kx(k是常数,k≠0)的图像是一条经过原点的直线,我们称它为直线y=kx.
k>0时,直线经过第一、三象限,y随x的增大而增大;
k<0时,直线经过第二、四象限,y随x的增大反而减小.
一次函数的图像与性质
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.一次函数:
(1)定义:
(当b=0时,y=kx+b变即y=kx,所以说正比例函数是一种特殊的一次函数)
(2)图像与性质:
一次函数y=kx+b(k≠0)的图像可以由直线y=kx平移|b|个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).一次函数y=kx+b(k≠0)的图像也是一条直线,我们称它为直线y=kx+b.
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
函数 字母系数取值 图像 经过的象限 函数性质
y=kx+b (k>0) b>0
b<0
y=kx+b (k<0) b>0
b<0
第一、二、三象限
第一、三、四象限
第一、二、四象限
第二、三、四象限
y随x增大而增大
y随x增大而减小
典型例题
当堂检测
学习目标
课堂总结
知识梳理
(3)直接列式法:
先设出函数表达式,再根据条件确定表达式中未知的系数,从而得出函数表达式的方法,叫做待定系数法.
由问题的实际意义直接写出.这种方法的实质是把问题中用文字叙述的数量关系用数学式子表达出来.
(4)待定系数法:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
正比例函数是一次函数的特例,它们之间是一般与特殊的关系.正比例函数具备一次函数所有的性质,它的特点在于图像必过原点,只需一个点的坐标就可以确定其表达式.
3.正比例函数与一次函数:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例1.已知y与x-1成正比例,且函数图像经过点(3,-6),求这个函数的表达式并画出这个函数图像.
解:设y=k(x-1)(k≠0),
把(3,-6)代入得:-6=k(3-1),
解得k=-3.
所以该函数的表达式是:y=-3x+3.
令x=0,则y=3.
所以该函数图像经过点(0,3),(3,-6).
其图像如图所示:
y=-3x+3
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.一次函数y=kx+b(k≠0),当x=-4时,y=6,且此函数的图像经过点(0,3).
(1)求此函数的表达式;
(2)画出函数的图像;
(3)若函数的图像与x轴y轴分别相交于点A、B,求△AOB的面积.
解:(1)根据题意,得:
解得:
∴一次函数的表达式为
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.一次函数y=kx+b(k≠0),当x=-4时,y=6,且此函数的图像经过点(0,3)
(1)求此函数的表达式;
(2)画出函数的图像;
(3)若函数的图像与x轴y轴分别相交于点A、B,求△AOB的面积.
解:(2)取两点A(4,0)和B(0,3)作直线AB即为
的图像.
(3)与x轴,y轴的交点坐标为(4,0)和(0,3)
所以S△AOB=
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例2.已知函数y=(3m+1)x+m-5.
(1)若函数图像经过原点,求m的值;
(2)若这个函数是一次函数,且y随着x的增大而增大,求m的取值范围.
解:(1)∵函数图像经过原点,
∴m-5=0,且3m+1≠0,
解得:m=5;
(2)∵y随着x的增大而增大,
∴3m+1>0,
解得:m> .
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.一次函数y=-x-2的图像经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3.在一次百米赛跑过程中,小明所跑过的路程s(m)与所用时间t(s)的关系如图所示.
(1)s是t的什么函数?
(2)写出s与t的函数关系式.
(3)小明此次比赛中的速度是多少?
解:(1)s是t的正比例函数;
(2)设函数表达式为s=kt,
14k=100,
(3)由路程=速度×时间可知,
解得k=
即:s= t(0≤t≤14)
速度v= (m/s)
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.一次函数与二元一次方程:
因为每个含有未知数x和y的二元一次方程都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.
方程组的解
对应两条直线交点的坐标
典型例题
当堂检测
学习目标
课堂总结
知识梳理
一次函数与二元一次方程的关系体现在:
(1)从形式上它们之间可以相互转化.
(2)以二元一次方程的解为坐标的点都在与它对应的函数图像上;反过来,一次函数图像上的点的坐标都是与它对应的二元一次方程的解.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例3.如图,直线l1的函数表达式为y=3x-2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(1)求点D和点C的坐标;
解:(1)∵在y=3x-2中,
令y=0,即3x-2=0
∵点C(m,3)在直线y=3x-2上,
∴3m-2=3,
解得:x= ,
∴D( ,0),
∴m= ,
∴C( ,3);
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例3.如图,直线l1的函数表达式为y=3x-2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(2)求直线l2的函数表达式;
(2)设直线l2的函数表达式为y=kx+b(K≠0),
由题意得:
解得:
∴
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例3.如图,直线l1的函数表达式为y=3x-2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(3)利用函数图像写出关于x,y的二元一次方程组.
(3)由图可知,二元一次方程组
的解为:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.图中两直线l1,l2的交点坐标可以看作哪组方程组的解( )
A. B.
C. D.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.如图,直线y=-2x+6与直线y=mx+n相交于点M(p,4).
(1)求p的值;
(2)直接写出关于x,y的二元一次方程组 的解;
(3)判断直线y=3nx+m-2n是否也过点M?并说明理由.
解:(1)∵直线y=-2x+6经过点M(p,4),
∴4=-2p+6,
(2)由图象可知方程组的解为 .
∴p=1.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.如图,直线y=-2x+6与直线y=mx+n相交于点M(p,4).
(3)判断直线y=3nx+m-2n是否也过点M?并说明理由.
(3)结论:直线y=3nx+m-2n经过点M,理由如下:
∵点M(1,4)在直线y=mx+n上,
∴m+n=4,
∴当x=1,时,y=3nx+m-2n=m+n=4,
∴直线y=3nx+m-2n经过点M.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例4.九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设x(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为y1千米,骑自行车学生骑行的路程为y2千米,y1、y2关于x的函数图象如图所示.
(1)求y2关于x的函数解析式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
典型例题
当堂检测
学习目标
课堂总结
知识梳理
(1)求y2关于x的函数表达式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
解:(1)设y2关于x的函数表达式是y2=kx+b,
即y2关于x的函数表达式是y2=0.2x-4,
得: ,
典型例题
当堂检测
学习目标
课堂总结
知识梳理
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
解:(2)由图像可知,
步行的学生的速度为:4÷40=0.1(千米/分钟)
∴步行同学到达百花公园的时间为:6÷0.1=60(分钟)
当y2=6时,6=0.2x-4,得x=50,
60-50=10(分钟),
答:骑自行车的学生先到达百花公园,先到了10分钟.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
6.李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图像如图所示,那么到达乙地时油箱剩余油量是多少升?
解:设一次函数的表达式为y=kx+b,
即到达乙地时油箱剩余油量是20升.
所以一次函数的表达式为y= x+35.
再将x=240代入 y= x+35,
得y= ×240+35=20,
将点(0,35),(160,25)代入,得: ,
解得:k= ,
典型例题
当堂检测
学习目标
课堂总结
知识梳理
7.有36名分别了多年的老同学商定到某个地方故地重游,他们决定租车前往,可租用的汽车有两种:甲种每辆可以乘8人,乙种每辆可以乘4人,他们不愿意让车子留空位子,但也不能超载.
(1)你能想出几种租车的方案?
解:(1)设每辆可乘8人的有x辆,每辆可乘4人的y辆.根据题意得:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
8x+4y=36
化简得:2x+y=9,
y=9-2x,
∵x,y都是正整数,
∴①x=1,y=7;
②x=2,y=5;
③x=3,y=3;
④x=4,y=1.
(2)已知可乘8人的车,每天租金为300元;可乘4人的车,每天租金为200元.请你帮助他们选择一个最便宜的租车方案.
(2)设总费用W元.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
则W=300x+200y=300x+200(9-2x)=-100x+1800.
W随x的增大而减小,则要使费用最小,则x取最大值:x=4.
故费用最低的方案为:乘8人的4辆,乘4人的1辆.
1.一次函数y=kx+b(k,b是常数,且k≠0)中的系数k与b决定着它的性质:
(1)当k>0时,y随x的增大而增大,图像从左向右是上升的;
(4)当b≠0时,直线y=kx+b一定不经过原点.
(3)当b=0时,一次函数y=kx+b化为正比例函数y=kx,它的图像一定经过原点;
(2)当k<0时,y随x的增大而减小,图像从左向右是下降的;
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.一次函数有着广泛的实际应用,掌握一次函数的应用有两个层次:
(1)若给出了一次函数的表达式,则可直接应用一次函数的性质解决问题;
(2)若问题只提供了一次函数的情境(有时是隐含的表述),则一般应先求出函数表达式,进而利用性质解决问题.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
复习课
第二十一章 一次函数
1.通过函数图像理解一次函数的性质
2.会用待定系数法求一次函数的表达式
3.知道一次函数与二元一次方程(组)之间的联系,并能解决相关问题
典型例题
当堂检测
学习目标
课堂总结
知识梳理
现实问题
一次函数
图像与性质
表达式
应用
一次函数与二元一次方程分关系
直接列式法
待定系数法
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.正比例函数:
(1)定义:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
(2)图像与性质:
一般地,正比例函数y=kx(k是常数,k≠0)的图像是一条经过原点的直线,我们称它为直线y=kx.
k>0时,直线经过第一、三象限,y随x的增大而增大;
k<0时,直线经过第二、四象限,y随x的增大反而减小.
一次函数的图像与性质
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.一次函数:
(1)定义:
(当b=0时,y=kx+b变即y=kx,所以说正比例函数是一种特殊的一次函数)
(2)图像与性质:
一次函数y=kx+b(k≠0)的图像可以由直线y=kx平移|b|个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).一次函数y=kx+b(k≠0)的图像也是一条直线,我们称它为直线y=kx+b.
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
函数 字母系数取值 图像 经过的象限 函数性质
y=kx+b (k>0) b>0
b<0
y=kx+b (k<0) b>0
b<0
第一、二、三象限
第一、三、四象限
第一、二、四象限
第二、三、四象限
y随x增大而增大
y随x增大而减小
典型例题
当堂检测
学习目标
课堂总结
知识梳理
(3)直接列式法:
先设出函数表达式,再根据条件确定表达式中未知的系数,从而得出函数表达式的方法,叫做待定系数法.
由问题的实际意义直接写出.这种方法的实质是把问题中用文字叙述的数量关系用数学式子表达出来.
(4)待定系数法:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
正比例函数是一次函数的特例,它们之间是一般与特殊的关系.正比例函数具备一次函数所有的性质,它的特点在于图像必过原点,只需一个点的坐标就可以确定其表达式.
3.正比例函数与一次函数:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例1.已知y与x-1成正比例,且函数图像经过点(3,-6),求这个函数的表达式并画出这个函数图像.
解:设y=k(x-1)(k≠0),
把(3,-6)代入得:-6=k(3-1),
解得k=-3.
所以该函数的表达式是:y=-3x+3.
令x=0,则y=3.
所以该函数图像经过点(0,3),(3,-6).
其图像如图所示:
y=-3x+3
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.一次函数y=kx+b(k≠0),当x=-4时,y=6,且此函数的图像经过点(0,3).
(1)求此函数的表达式;
(2)画出函数的图像;
(3)若函数的图像与x轴y轴分别相交于点A、B,求△AOB的面积.
解:(1)根据题意,得:
解得:
∴一次函数的表达式为
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.一次函数y=kx+b(k≠0),当x=-4时,y=6,且此函数的图像经过点(0,3)
(1)求此函数的表达式;
(2)画出函数的图像;
(3)若函数的图像与x轴y轴分别相交于点A、B,求△AOB的面积.
解:(2)取两点A(4,0)和B(0,3)作直线AB即为
的图像.
(3)与x轴,y轴的交点坐标为(4,0)和(0,3)
所以S△AOB=
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例2.已知函数y=(3m+1)x+m-5.
(1)若函数图像经过原点,求m的值;
(2)若这个函数是一次函数,且y随着x的增大而增大,求m的取值范围.
解:(1)∵函数图像经过原点,
∴m-5=0,且3m+1≠0,
解得:m=5;
(2)∵y随着x的增大而增大,
∴3m+1>0,
解得:m> .
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.一次函数y=-x-2的图像经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3.在一次百米赛跑过程中,小明所跑过的路程s(m)与所用时间t(s)的关系如图所示.
(1)s是t的什么函数?
(2)写出s与t的函数关系式.
(3)小明此次比赛中的速度是多少?
解:(1)s是t的正比例函数;
(2)设函数表达式为s=kt,
14k=100,
(3)由路程=速度×时间可知,
解得k=
即:s= t(0≤t≤14)
速度v= (m/s)
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.一次函数与二元一次方程:
因为每个含有未知数x和y的二元一次方程都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.
方程组的解
对应两条直线交点的坐标
典型例题
当堂检测
学习目标
课堂总结
知识梳理
一次函数与二元一次方程的关系体现在:
(1)从形式上它们之间可以相互转化.
(2)以二元一次方程的解为坐标的点都在与它对应的函数图像上;反过来,一次函数图像上的点的坐标都是与它对应的二元一次方程的解.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例3.如图,直线l1的函数表达式为y=3x-2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(1)求点D和点C的坐标;
解:(1)∵在y=3x-2中,
令y=0,即3x-2=0
∵点C(m,3)在直线y=3x-2上,
∴3m-2=3,
解得:x= ,
∴D( ,0),
∴m= ,
∴C( ,3);
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例3.如图,直线l1的函数表达式为y=3x-2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(2)求直线l2的函数表达式;
(2)设直线l2的函数表达式为y=kx+b(K≠0),
由题意得:
解得:
∴
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例3.如图,直线l1的函数表达式为y=3x-2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(3)利用函数图像写出关于x,y的二元一次方程组.
(3)由图可知,二元一次方程组
的解为:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.图中两直线l1,l2的交点坐标可以看作哪组方程组的解( )
A. B.
C. D.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.如图,直线y=-2x+6与直线y=mx+n相交于点M(p,4).
(1)求p的值;
(2)直接写出关于x,y的二元一次方程组 的解;
(3)判断直线y=3nx+m-2n是否也过点M?并说明理由.
解:(1)∵直线y=-2x+6经过点M(p,4),
∴4=-2p+6,
(2)由图象可知方程组的解为 .
∴p=1.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.如图,直线y=-2x+6与直线y=mx+n相交于点M(p,4).
(3)判断直线y=3nx+m-2n是否也过点M?并说明理由.
(3)结论:直线y=3nx+m-2n经过点M,理由如下:
∵点M(1,4)在直线y=mx+n上,
∴m+n=4,
∴当x=1,时,y=3nx+m-2n=m+n=4,
∴直线y=3nx+m-2n经过点M.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例4.九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设x(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为y1千米,骑自行车学生骑行的路程为y2千米,y1、y2关于x的函数图象如图所示.
(1)求y2关于x的函数解析式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
典型例题
当堂检测
学习目标
课堂总结
知识梳理
(1)求y2关于x的函数表达式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
解:(1)设y2关于x的函数表达式是y2=kx+b,
即y2关于x的函数表达式是y2=0.2x-4,
得: ,
典型例题
当堂检测
学习目标
课堂总结
知识梳理
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
解:(2)由图像可知,
步行的学生的速度为:4÷40=0.1(千米/分钟)
∴步行同学到达百花公园的时间为:6÷0.1=60(分钟)
当y2=6时,6=0.2x-4,得x=50,
60-50=10(分钟),
答:骑自行车的学生先到达百花公园,先到了10分钟.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
6.李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图像如图所示,那么到达乙地时油箱剩余油量是多少升?
解:设一次函数的表达式为y=kx+b,
即到达乙地时油箱剩余油量是20升.
所以一次函数的表达式为y= x+35.
再将x=240代入 y= x+35,
得y= ×240+35=20,
将点(0,35),(160,25)代入,得: ,
解得:k= ,
典型例题
当堂检测
学习目标
课堂总结
知识梳理
7.有36名分别了多年的老同学商定到某个地方故地重游,他们决定租车前往,可租用的汽车有两种:甲种每辆可以乘8人,乙种每辆可以乘4人,他们不愿意让车子留空位子,但也不能超载.
(1)你能想出几种租车的方案?
解:(1)设每辆可乘8人的有x辆,每辆可乘4人的y辆.根据题意得:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
8x+4y=36
化简得:2x+y=9,
y=9-2x,
∵x,y都是正整数,
∴①x=1,y=7;
②x=2,y=5;
③x=3,y=3;
④x=4,y=1.
(2)已知可乘8人的车,每天租金为300元;可乘4人的车,每天租金为200元.请你帮助他们选择一个最便宜的租车方案.
(2)设总费用W元.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
则W=300x+200y=300x+200(9-2x)=-100x+1800.
W随x的增大而减小,则要使费用最小,则x取最大值:x=4.
故费用最低的方案为:乘8人的4辆,乘4人的1辆.
1.一次函数y=kx+b(k,b是常数,且k≠0)中的系数k与b决定着它的性质:
(1)当k>0时,y随x的增大而增大,图像从左向右是上升的;
(4)当b≠0时,直线y=kx+b一定不经过原点.
(3)当b=0时,一次函数y=kx+b化为正比例函数y=kx,它的图像一定经过原点;
(2)当k<0时,y随x的增大而减小,图像从左向右是下降的;
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.一次函数有着广泛的实际应用,掌握一次函数的应用有两个层次:
(1)若给出了一次函数的表达式,则可直接应用一次函数的性质解决问题;
(2)若问题只提供了一次函数的情境(有时是隐含的表述),则一般应先求出函数表达式,进而利用性质解决问题.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
