7.1 命题 第2课时 课件(共14张PPT) 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 7.1 命题 第2课时 课件(共14张PPT) 2023-2024学年初中数学冀教版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 840.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:29:15 | ||
图片预览




文档简介
(共14张PPT)
第七章 相交线与平行线
7.1 命题
第2课时
一、学习目标
1.掌握说理、基本事实、定理及演绎推理的概念.(重点)
2.体会命题演绎推理的过程,体验数学思维的严谨性.
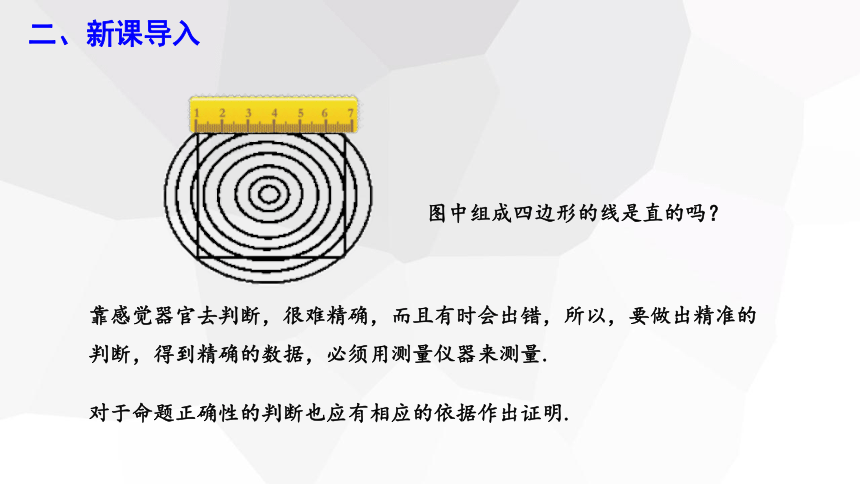
二、新课导入
靠感觉器官去判断,很难精确,而且有时会出错,所以,要做出精准的判断,得到精确的数据,必须用测量仪器来测量.
图中组成四边形的线是直的吗?
对于命题正确性的判断也应有相应的依据作出证明.
三、概念剖析
(一)说理和基本事实
有些命题经过实践检验被认为真命题,我们把这样的命题叫做基本事实.
由观察、实验、归纳和类比等方法得出的命题,可能是真命题,也可能是假命题.判断命题的真假需要说明理由,这个过程就是说理.
如“过平面上两点,有且只有一条直线”.
三、概念剖析
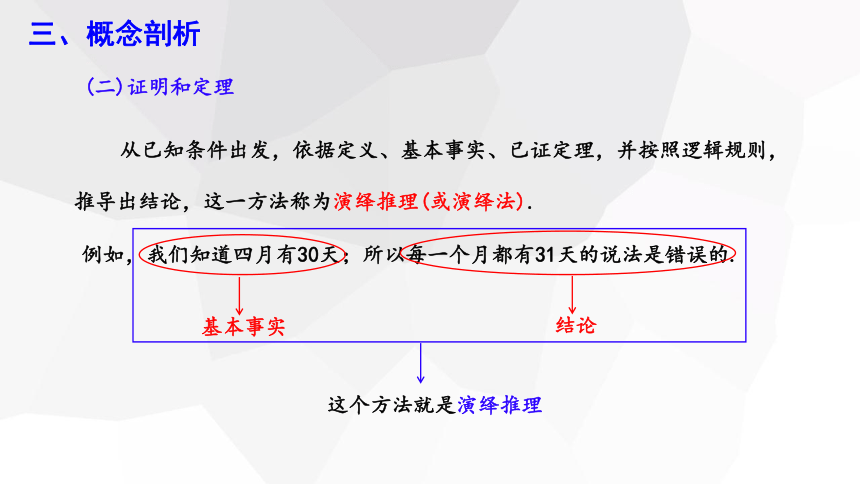
(二)证明和定理
从已知条件出发,依据定义、基本事实、已证定理,并按照逻辑规则,推导出结论,这一方法称为演绎推理(或演绎法).
例如,我们知道四月有30天;所以每一个月都有31天的说法是错误的.
基本事实
结论
这个方法就是演绎推理
归纳总结
三、概念剖析
证实其他命题的正确性
推 理
基本事实或定理
一些条件
+
有些真命题,它们的正确性已经过演绎推理得到证实,并被作为判定其他命题真假的依据,这些命题叫做定理.
三、概念剖析
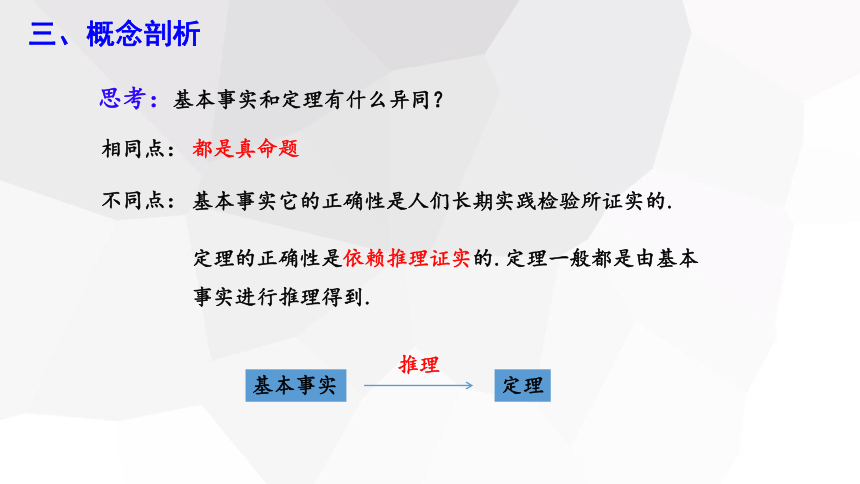
思考:基本事实和定理有什么异同?
基本事实
定理
推理
相同点:
都是真命题
不同点:
基本事实它的正确性是人们长期实践检验所证实的.
定理的正确性是依赖推理证实的.定理一般都是由基本事实进行推理得到.
四、典型例题
例1.如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么“AD=CB”是真命题.
A
C
D
B
理由:因为 AC=DB(已知),
所以 AC+CD=DB+CD(等量加等量,和相等),
所以 AD=CB(线段和的定义).
四、典型例题
归纳总结
演绎推理中每一步的推理要有根据.说理的依据是基本事实、有关概念的定义、已知的定理、推论及已知条件.初学时,把依据写在每一步的推理后面.
【当堂检测】
1.“a2>a”是真命题还是假命题?请说明理由.
解:假命题;
理由:存在反例,
若a=1时,a2=a=1.
2.阅读下面命题及其说理过程,在括号内填上推理的依据.
命题:如图,如果∠ABC=∠A'B'C',∠1=∠2,那么∠3=∠4.
理由: 因为∠ABC=∠A'B'C',∠1=∠2,( )
已知
【当堂检测】
C
A
B
1
3
D
C'
A'
B'
2
4
D'
所以∠ABC-∠1=∠A'B'C'-∠2( ).
等式的性质
又因为∠3=∠ABC-∠1,∠4=∠A'B'C'-∠2(两角差的定义)
所以∠3=∠4( 等量代换 ).
【当堂检测】
3.对“如果∠1和∠2都是∠α的余角,那么∠1=∠2”的说理过程,在括
号内填上依据.
理由:因为∠1+∠α=90°(已知),
因为∠2+∠α=90°( )
所以∠1=90°-∠α(等式的性质)
所以∠2=90°-∠α( )
所以∠1=∠2( )
2
α
1
已知
等式的性质
等量代换
【当堂检测】
4.说明“一个偶数前后相邻的两个偶数之和,一定是4的倍数”是一个
真命题.
解:设中间的偶数为2n(n为整数),
则与2n前后相邻的两个偶数分别为2n-2,2n+2,
则有2n-2+2n+2=4n.
因为4n是4的倍数,
所以“一个偶数前后相邻的两个偶数之和,一定是4的倍数”是真命题.
五、课堂总结
已知条件
结论
依据定义、基本事实,已证定理
定理
演绎推理
说理
经过证明的真命题称为定理
从已知条件出发,依据定义、基本事实,已证定理推导出
结论的方法
判断命题的真假,说明理由.
第七章 相交线与平行线
7.1 命题
第2课时
一、学习目标
1.掌握说理、基本事实、定理及演绎推理的概念.(重点)
2.体会命题演绎推理的过程,体验数学思维的严谨性.
二、新课导入
靠感觉器官去判断,很难精确,而且有时会出错,所以,要做出精准的判断,得到精确的数据,必须用测量仪器来测量.
图中组成四边形的线是直的吗?
对于命题正确性的判断也应有相应的依据作出证明.
三、概念剖析
(一)说理和基本事实
有些命题经过实践检验被认为真命题,我们把这样的命题叫做基本事实.
由观察、实验、归纳和类比等方法得出的命题,可能是真命题,也可能是假命题.判断命题的真假需要说明理由,这个过程就是说理.
如“过平面上两点,有且只有一条直线”.
三、概念剖析
(二)证明和定理
从已知条件出发,依据定义、基本事实、已证定理,并按照逻辑规则,推导出结论,这一方法称为演绎推理(或演绎法).
例如,我们知道四月有30天;所以每一个月都有31天的说法是错误的.
基本事实
结论
这个方法就是演绎推理
归纳总结
三、概念剖析
证实其他命题的正确性
推 理
基本事实或定理
一些条件
+
有些真命题,它们的正确性已经过演绎推理得到证实,并被作为判定其他命题真假的依据,这些命题叫做定理.
三、概念剖析
思考:基本事实和定理有什么异同?
基本事实
定理
推理
相同点:
都是真命题
不同点:
基本事实它的正确性是人们长期实践检验所证实的.
定理的正确性是依赖推理证实的.定理一般都是由基本事实进行推理得到.
四、典型例题
例1.如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么“AD=CB”是真命题.
A
C
D
B
理由:因为 AC=DB(已知),
所以 AC+CD=DB+CD(等量加等量,和相等),
所以 AD=CB(线段和的定义).
四、典型例题
归纳总结
演绎推理中每一步的推理要有根据.说理的依据是基本事实、有关概念的定义、已知的定理、推论及已知条件.初学时,把依据写在每一步的推理后面.
【当堂检测】
1.“a2>a”是真命题还是假命题?请说明理由.
解:假命题;
理由:存在反例,
若a=1时,a2=a=1.
2.阅读下面命题及其说理过程,在括号内填上推理的依据.
命题:如图,如果∠ABC=∠A'B'C',∠1=∠2,那么∠3=∠4.
理由: 因为∠ABC=∠A'B'C',∠1=∠2,( )
已知
【当堂检测】
C
A
B
1
3
D
C'
A'
B'
2
4
D'
所以∠ABC-∠1=∠A'B'C'-∠2( ).
等式的性质
又因为∠3=∠ABC-∠1,∠4=∠A'B'C'-∠2(两角差的定义)
所以∠3=∠4( 等量代换 ).
【当堂检测】
3.对“如果∠1和∠2都是∠α的余角,那么∠1=∠2”的说理过程,在括
号内填上依据.
理由:因为∠1+∠α=90°(已知),
因为∠2+∠α=90°( )
所以∠1=90°-∠α(等式的性质)
所以∠2=90°-∠α( )
所以∠1=∠2( )
2
α
1
已知
等式的性质
等量代换
【当堂检测】
4.说明“一个偶数前后相邻的两个偶数之和,一定是4的倍数”是一个
真命题.
解:设中间的偶数为2n(n为整数),
则与2n前后相邻的两个偶数分别为2n-2,2n+2,
则有2n-2+2n+2=4n.
因为4n是4的倍数,
所以“一个偶数前后相邻的两个偶数之和,一定是4的倍数”是真命题.
五、课堂总结
已知条件
结论
依据定义、基本事实,已证定理
定理
演绎推理
说理
经过证明的真命题称为定理
从已知条件出发,依据定义、基本事实,已证定理推导出
结论的方法
判断命题的真假,说明理由.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
