7.2 相交线 第1课时 课件(共19张PPT) 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 7.2 相交线 第1课时 课件(共19张PPT) 2023-2024学年初中数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 921.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:29:00 | ||
图片预览



文档简介
(共19张PPT)
第七章 相交线与平行线
7.2 相交线
第1课时
1.掌握对顶角的概念及其性质.
一、学习目标
2.理解掌握同位角、内错角、同旁内角的概念.
二、新课导入
观察:在同一个平面内,两条直线的位置关系只有相交和不相交,你能根据图中的提示画出相交线吗?
三、概念剖析
两直线相交只有一个交点,那么两直线相交形成了几个角呢?
A
B
C
D
很显然,两直线相交形成了4个角,我们用∠1,∠2,∠3,∠4表示.
1
3
2
4
可以发现∠1和∠3、∠2和∠4是相对的两个角.
两条直线相交有几个交点?
只有一个交点
三、概念剖析
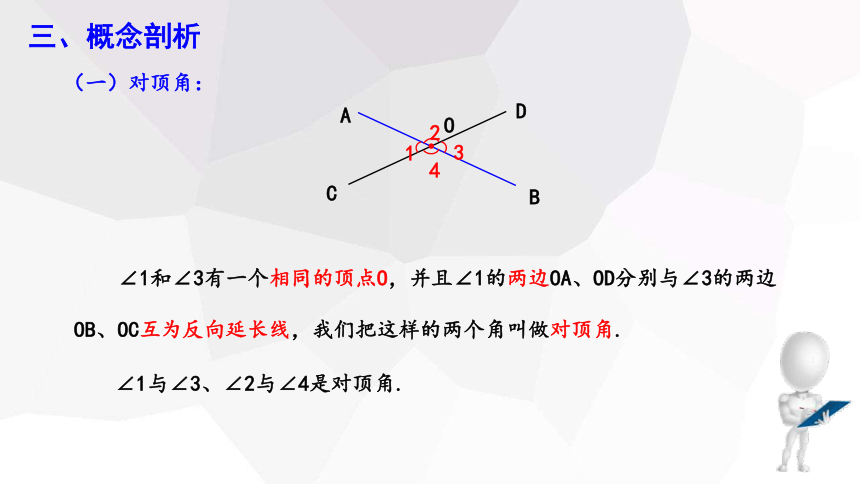
∠1和∠3有一个相同的顶点O,并且∠1的两边OA、OD分别与∠3的两边OB、OC互为反向延长线,我们把这样的两个角叫做对顶角.
A
B
C
D
1
3
2
4
O
∠1与∠3、∠2与∠4是对顶角.
(一)对顶角:
其实对于任意两条直线相交所形成的对顶角,由于他们都有一个相同的补角,
所以他们是相等的.
A
B
C
D
1
3
2
4
O
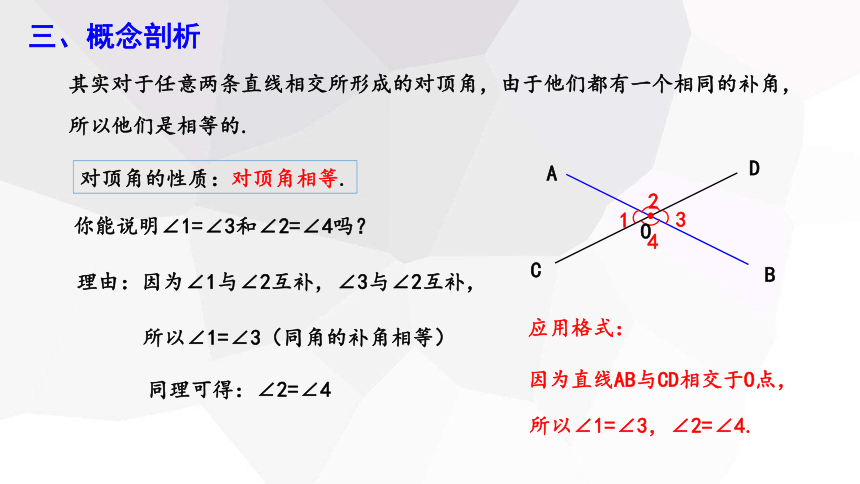
对顶角的性质:对顶角相等.
三、概念剖析
你能说明∠1=∠3和∠2=∠4吗?
理由:因为∠1与∠2互补,∠3与∠2互补,
应用格式:
因为直线AB与CD相交于O点,
所以∠1=∠3(同角的补角相等)
同理可得:∠2=∠4
所以∠1=∠3,∠2=∠4.
B
F
E
2
3
1
4
A
O
C
D
6
7
5
8
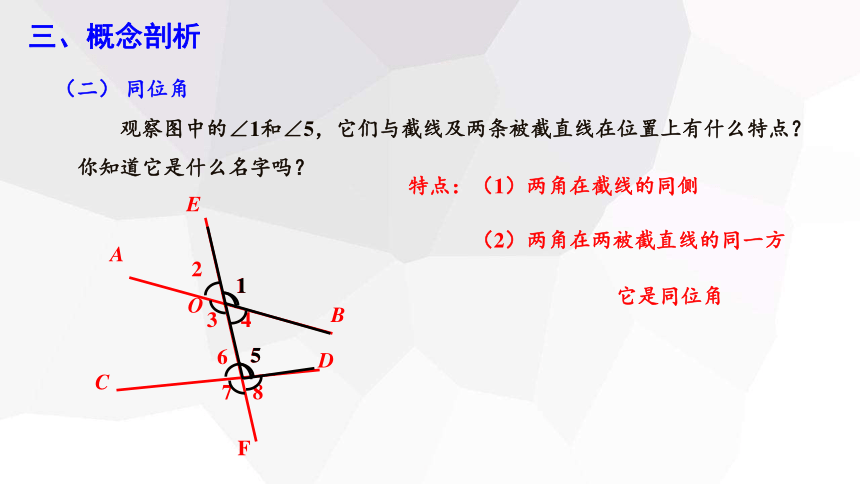
观察图中的∠1和∠5,它们与截线及两条被截直线在位置上有什么特点?你知道它是什么名字吗?
特点:(1)两角在截线的同侧
(2)两角在两被截直线的同一方
它是同位角
1
5
(二) 同位角
三、概念剖析
三、概念剖析
请判断下面各个图中∠1与∠2是同位角吗?你能联想一个字母,用它来形象化地反映同位角的图形特征吗?
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的______, 在截线的______. 形如字母_____
“F”
同侧
同侧
都是同位角
三、概念剖析
B
F
E
2
3
1
4
A
O
C
D
6
7
5
8
观察图中的∠3和∠5,它们与截线及两条被截直线在位置上有什么特点?你知道它是什么名字吗?
特征:(1)两角在截线的两侧
(2)两角在两被截直线之间
它是内错角
5
3
(三)内错角
三、概念剖析
你能联想一个字母,用它来形象化地反映内错角的图形特征吗?
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的______, 在截线的______ 形如字母_____
在两条被截直线的______, 在截线的______ 形如字母_____
“F”
同侧
同侧
内错角
之间
两侧
“Z”
三、概念剖析
B
F
E
2
3
1
4
A
O
C
D
6
7
5
8
观察图中的∠4和∠5,它们与截线及两条被截直线在位置上有什么特点?你知道它是什么名字吗?
特征:(1)两角在截线的同侧
(2)两角在两被截 直线之间
它是同旁内角
5
4
(四)同旁内角
三、概念剖析
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的______, 在截线的______ 形如字母___
在两条被截直线的______, 在截线的______ 形如字母___
在两条被截直线的______, 在截线的_____ 形如字母___
“F”
同侧
同侧
内错角
之间
两侧
“Z”
同旁内角
之间
同侧
“U”
典型例题
例1.下列各图中,∠1与∠2是对顶角的是( )
C
D
D
A
B
1
2
1
2
1
2
1
2
方法总结:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.
辨认对顶角的要领:
一看是不是两条直线相交所成的角,对顶角与相交线是唇齿相依,哪里
有相交直线,哪里就有对顶角,反过来,哪里有对顶角,哪里就有相交线;
二看是不是有公共顶点;
三看是不是没有公共边,符合这三个条件时,才能确定这两个角是对顶
角,只具备一个或两个条件都不行.
典型例题
解析:因为AB、CD、EF相交于O点,∠1=35°,∠2=35°(已知),
例2.如图,已知,AB、CD、EF相交于O点,∠1=35°,∠2=35°,则∠3的度数是_________.
所以∠BOC=180°-∠1-∠2=110°(平角的定义),
因为∠3与∠BOC是对顶角(已知),
所以∠3=∠BOC=110°(对顶角相等).
110°
典型例题
【当堂检测】
1.如图,直线AB、CD、EF相交于点O.
(1)请写出∠AOC,∠AOE,∠EOC的对顶角;
(2)若∠AOC=50°,求∠BOD,∠BOC的度数.
解:(1)∠AOC的对顶角是∠BOD,∠AOE的对顶角是∠BOF,∠EOC的对顶角是∠DOF;
(2)∵∠AOC=50°(已知),
所以∠BOD=50°(对顶角相等),
∠BOC=180°-50°=130°(两角差的定义).
解:∠1和∠2是同位角,是由直线CD、FE被AB截成的;
例3.如图,∠ 1和∠ 2是什么角?∠ 2和∠ 3呢?∠ 4和∠ 5呢?它们分别是由哪两条直线被哪一条直线截成的?
A
B
C
D
E
F
⌒
3
⌒
2
A
B
C
D
E
F
⌒
1
⌒
2
A
B
C
D
E
F
⌒
4
⌒
5
G
∠2和∠3是内错角,是由直线AB、CD被EF截成的;
∠4和∠5是同旁内角,是由直线AB 、EF被CD截成的.
典型例题
2.如图,直线DE截直线AB,AC指出所有的同位角、内错角和同旁内角.
解:同位角
内错角
同旁内角
∠2和∠5
∠1和∠8
∠3和∠6
∠4和∠7
∠4和∠5
∠1和∠6
∠1和∠5
∠4和∠6
∠1和∠A
∠5和∠A
∠4和∠A
∠6和∠A
【当堂检测】
∠2和∠A
∠8和∠A
四、课堂总结
对顶角和三线八角
三线八角
定义
性质
具有公共定点,两边互为反向延长线
对顶角相等
同位角
同旁内角
内错角
F形
U形
Z形
对顶角
第七章 相交线与平行线
7.2 相交线
第1课时
1.掌握对顶角的概念及其性质.
一、学习目标
2.理解掌握同位角、内错角、同旁内角的概念.
二、新课导入
观察:在同一个平面内,两条直线的位置关系只有相交和不相交,你能根据图中的提示画出相交线吗?
三、概念剖析
两直线相交只有一个交点,那么两直线相交形成了几个角呢?
A
B
C
D
很显然,两直线相交形成了4个角,我们用∠1,∠2,∠3,∠4表示.
1
3
2
4
可以发现∠1和∠3、∠2和∠4是相对的两个角.
两条直线相交有几个交点?
只有一个交点
三、概念剖析
∠1和∠3有一个相同的顶点O,并且∠1的两边OA、OD分别与∠3的两边OB、OC互为反向延长线,我们把这样的两个角叫做对顶角.
A
B
C
D
1
3
2
4
O
∠1与∠3、∠2与∠4是对顶角.
(一)对顶角:
其实对于任意两条直线相交所形成的对顶角,由于他们都有一个相同的补角,
所以他们是相等的.
A
B
C
D
1
3
2
4
O
对顶角的性质:对顶角相等.
三、概念剖析
你能说明∠1=∠3和∠2=∠4吗?
理由:因为∠1与∠2互补,∠3与∠2互补,
应用格式:
因为直线AB与CD相交于O点,
所以∠1=∠3(同角的补角相等)
同理可得:∠2=∠4
所以∠1=∠3,∠2=∠4.
B
F
E
2
3
1
4
A
O
C
D
6
7
5
8
观察图中的∠1和∠5,它们与截线及两条被截直线在位置上有什么特点?你知道它是什么名字吗?
特点:(1)两角在截线的同侧
(2)两角在两被截直线的同一方
它是同位角
1
5
(二) 同位角
三、概念剖析
三、概念剖析
请判断下面各个图中∠1与∠2是同位角吗?你能联想一个字母,用它来形象化地反映同位角的图形特征吗?
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的______, 在截线的______. 形如字母_____
“F”
同侧
同侧
都是同位角
三、概念剖析
B
F
E
2
3
1
4
A
O
C
D
6
7
5
8
观察图中的∠3和∠5,它们与截线及两条被截直线在位置上有什么特点?你知道它是什么名字吗?
特征:(1)两角在截线的两侧
(2)两角在两被截直线之间
它是内错角
5
3
(三)内错角
三、概念剖析
你能联想一个字母,用它来形象化地反映内错角的图形特征吗?
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的______, 在截线的______ 形如字母_____
在两条被截直线的______, 在截线的______ 形如字母_____
“F”
同侧
同侧
内错角
之间
两侧
“Z”
三、概念剖析
B
F
E
2
3
1
4
A
O
C
D
6
7
5
8
观察图中的∠4和∠5,它们与截线及两条被截直线在位置上有什么特点?你知道它是什么名字吗?
特征:(1)两角在截线的同侧
(2)两角在两被截 直线之间
它是同旁内角
5
4
(四)同旁内角
三、概念剖析
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的______, 在截线的______ 形如字母___
在两条被截直线的______, 在截线的______ 形如字母___
在两条被截直线的______, 在截线的_____ 形如字母___
“F”
同侧
同侧
内错角
之间
两侧
“Z”
同旁内角
之间
同侧
“U”
典型例题
例1.下列各图中,∠1与∠2是对顶角的是( )
C
D
D
A
B
1
2
1
2
1
2
1
2
方法总结:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.
辨认对顶角的要领:
一看是不是两条直线相交所成的角,对顶角与相交线是唇齿相依,哪里
有相交直线,哪里就有对顶角,反过来,哪里有对顶角,哪里就有相交线;
二看是不是有公共顶点;
三看是不是没有公共边,符合这三个条件时,才能确定这两个角是对顶
角,只具备一个或两个条件都不行.
典型例题
解析:因为AB、CD、EF相交于O点,∠1=35°,∠2=35°(已知),
例2.如图,已知,AB、CD、EF相交于O点,∠1=35°,∠2=35°,则∠3的度数是_________.
所以∠BOC=180°-∠1-∠2=110°(平角的定义),
因为∠3与∠BOC是对顶角(已知),
所以∠3=∠BOC=110°(对顶角相等).
110°
典型例题
【当堂检测】
1.如图,直线AB、CD、EF相交于点O.
(1)请写出∠AOC,∠AOE,∠EOC的对顶角;
(2)若∠AOC=50°,求∠BOD,∠BOC的度数.
解:(1)∠AOC的对顶角是∠BOD,∠AOE的对顶角是∠BOF,∠EOC的对顶角是∠DOF;
(2)∵∠AOC=50°(已知),
所以∠BOD=50°(对顶角相等),
∠BOC=180°-50°=130°(两角差的定义).
解:∠1和∠2是同位角,是由直线CD、FE被AB截成的;
例3.如图,∠ 1和∠ 2是什么角?∠ 2和∠ 3呢?∠ 4和∠ 5呢?它们分别是由哪两条直线被哪一条直线截成的?
A
B
C
D
E
F
⌒
3
⌒
2
A
B
C
D
E
F
⌒
1
⌒
2
A
B
C
D
E
F
⌒
4
⌒
5
G
∠2和∠3是内错角,是由直线AB、CD被EF截成的;
∠4和∠5是同旁内角,是由直线AB 、EF被CD截成的.
典型例题
2.如图,直线DE截直线AB,AC指出所有的同位角、内错角和同旁内角.
解:同位角
内错角
同旁内角
∠2和∠5
∠1和∠8
∠3和∠6
∠4和∠7
∠4和∠5
∠1和∠6
∠1和∠5
∠4和∠6
∠1和∠A
∠5和∠A
∠4和∠A
∠6和∠A
【当堂检测】
∠2和∠A
∠8和∠A
四、课堂总结
对顶角和三线八角
三线八角
定义
性质
具有公共定点,两边互为反向延长线
对顶角相等
同位角
同旁内角
内错角
F形
U形
Z形
对顶角
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
