8.3 同底数幂的除法 课件(共17张PPT) 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 8.3 同底数幂的除法 课件(共17张PPT) 2023-2024学年初中数学冀教版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第八章 整式的乘法
8.3 同底数幂的除法
2.能够利用同底数幂的除法法则进行运算.(重点)
1.知道同底数幂的除法法则;
一、学习目标
二、新课导入
世界上的最快速度
海洋生物:旗鱼
105m/h
陆地生物:猎豹
1.2×105m/h
飞行生物:游隼
3.9×105m/h
新型飞机
107m/h
你知道新型飞机速度是旗鱼速度的多少倍吗?
107÷105
=?
三、概念剖析
在整式的运算中,当然也会遇到两个同底数幂相除的情况,例如前面出现的
参照同底数幂的乘法运算,我们该如何去进行计算呢?
前面我们已经学习了同底数幂的乘法运算.
我们先来完成下表的填空.
同底数幂的乘法法则:同底数幂相乘, 不变, 相加.
用字母表示为: .
am·an=am+n(m,n都是正整数)
底数
指数
107÷105.
三、概念剖析
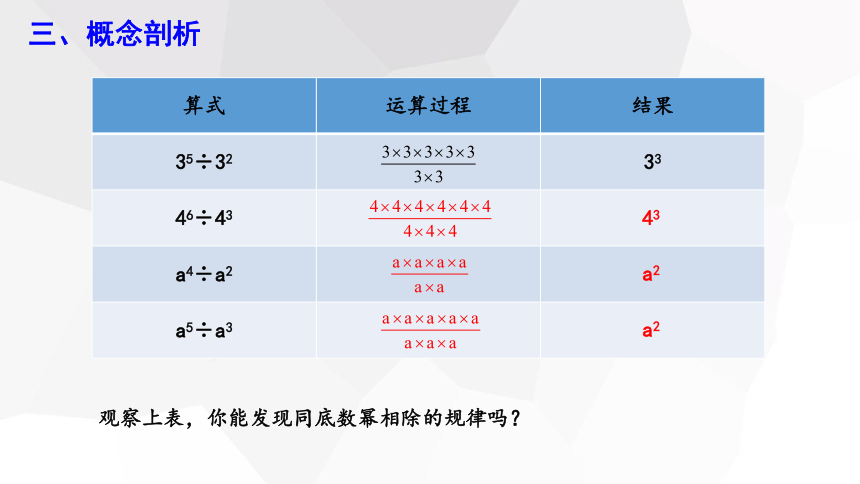
算式 运算过程 结果
35÷32 33
46÷43
a4÷a2
a5÷a3
43
a2
a2
观察上表,你能发现同底数幂相除的规律吗?
三、概念剖析
由此得幂的运算性质4:
am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
即同底数幂相除,底数不变,指数相减.
这里a≠0是因为:当a=0时,an=0,而0不能作为除数;故a不能为0.
一般地,如果字母m,n都是正整数(m>n),那么
am÷an=
(a·a·...·a)÷(a·a·...·a)
m个a
n个a
=a·a·...·a
(m-n)个a
三、概念剖析
(a≠0,p是正整数),
已知:m,n是正整数,a≠0,为了使am÷an=am-n在m≤n时仍然成立:
(1)当m<n时,m-n<0,应该如何规定am-n的意义?
(2)当m=n时,m-n=0,应该如何规定a0的意义?
我们规定:
a0=1(a≠0),
即任何一个不等于零的数的零次幂都等于1.
即任何一个不等于零的数的-p(p是正整数)次幂,等于这个数的p次幂的倒数.
am÷an=am-n(a≠0,m,n都是正整数).
这样,对于任何正整数m,n,都有
例1 计算:
(1)106÷102 (2)23÷25
(3)5m÷5m-1 (4)an÷an+1(a≠0)
典型例题
解:(1)106÷102
(2)23÷25
=106-2
=104
=23-5
=2-2
(3)5m÷5m-1
=5m-(m-1)
=5
(4)an÷an+1
=an-(n+1)
=a-1
【当堂检测】
1.判断.
(1)a4÷a3=a7
(2)a2÷a5=a10
(3)(-b)4÷(-b)2=-b2
(4)(-1)0=-1
×
×
×
a4÷a3=a
a2÷a5=a-3
(-b)4÷(-b)2=b4÷b2=b2
×
(-1)0=1
2.计算.
【当堂检测】
(2)m5÷m2
(4)(x2)2·x÷x5
(1)x7÷x3
(1)原式=x7-3=x4
(2)原式=m5-2=m3
(3)原式=(xy)7-6=xy
(4)原式=x5-5=1
(3)(xy)7÷(xy)6
解:
例2 计算:
(1)a8÷a2÷a3 (2)(-x)9÷(-x)5÷(-x)3
解:(1)原式=a8-2÷a3
=a8-2-3
总结:由同底数幂相除的法则,我们可以推出:
am÷an÷aq=am-n-q(a≠0,m,n,q都是正整数).
(2)原式=(-x)9-5÷(-x)3
=a3
=(-x)9-5-3
=-x
典型例题
3.计算.
【当堂检测】
(1)(x-y)9÷(y-x)6÷(x-y)
(1)原式=(x-y)9-6-1 =(x-y)2
(2)原式=(xy)7-6-3 =(xy)-2=
(2)(xy)7÷(xy)6÷(xy)3
解:
例3.已知:xa=4,xb=9,求:(1)xa-b;(2)x3a-2b.
分析:因为xa÷xb=xa-b,所以xa-b=xa÷xb.
解:
(2)因为xa=4,xb=9,
总结:可逆用同底数幂相除的法则进行求值:
am-n=am÷an(a≠0,m,n都是正整数).
(1)因为xa=4,xb=9;
所以xa-b=xa÷xb
所以x3a-2b=x3a÷x2b
所以x3a=(xa)3=64,x2b=(xb)2=81;
典型例题
4.如果3m=10,3n=5,那么3m-n的值为多少?
【当堂检测】
解:当3m=10,3n=5,
原式=3m÷3n
=10÷5
=2
故3m-n的值2.
典型例题
例4.计算:
(1)x3 x5-(2x4)2+x10÷x2.
(2)(x-y)9÷(y-x)6·(x-y)
解:
(2)原式=(x-y)9÷(x-y)6·(x-y)
(1)原式=x8-4x8+x8
注意:计算时要先将互为相反数的底数转化为相同的底数.
=-2x8
=(x-y)4
5.计算:
(1)22020×0.52018÷22
(2)(a3)2÷(a4·a2)
【当堂检测】
解:
(1)原式=22×(22018×0.52018)÷22
=1
(2)原式=a6÷a6
=a6-6
=1
=22×(2×0.5)2018÷22
四、课堂总结
同底数幂的除法
法则
am÷an=am-n (a≠0,m,n都是正整数)
零指数幂和负指数幂
同底数幂相除,底数不变,指数相减
a0=1 (a≠0)
(a≠0,p是正整数)
第八章 整式的乘法
8.3 同底数幂的除法
2.能够利用同底数幂的除法法则进行运算.(重点)
1.知道同底数幂的除法法则;
一、学习目标
二、新课导入
世界上的最快速度
海洋生物:旗鱼
105m/h
陆地生物:猎豹
1.2×105m/h
飞行生物:游隼
3.9×105m/h
新型飞机
107m/h
你知道新型飞机速度是旗鱼速度的多少倍吗?
107÷105
=?
三、概念剖析
在整式的运算中,当然也会遇到两个同底数幂相除的情况,例如前面出现的
参照同底数幂的乘法运算,我们该如何去进行计算呢?
前面我们已经学习了同底数幂的乘法运算.
我们先来完成下表的填空.
同底数幂的乘法法则:同底数幂相乘, 不变, 相加.
用字母表示为: .
am·an=am+n(m,n都是正整数)
底数
指数
107÷105.
三、概念剖析
算式 运算过程 结果
35÷32 33
46÷43
a4÷a2
a5÷a3
43
a2
a2
观察上表,你能发现同底数幂相除的规律吗?
三、概念剖析
由此得幂的运算性质4:
am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
即同底数幂相除,底数不变,指数相减.
这里a≠0是因为:当a=0时,an=0,而0不能作为除数;故a不能为0.
一般地,如果字母m,n都是正整数(m>n),那么
am÷an=
(a·a·...·a)÷(a·a·...·a)
m个a
n个a
=a·a·...·a
(m-n)个a
三、概念剖析
(a≠0,p是正整数),
已知:m,n是正整数,a≠0,为了使am÷an=am-n在m≤n时仍然成立:
(1)当m<n时,m-n<0,应该如何规定am-n的意义?
(2)当m=n时,m-n=0,应该如何规定a0的意义?
我们规定:
a0=1(a≠0),
即任何一个不等于零的数的零次幂都等于1.
即任何一个不等于零的数的-p(p是正整数)次幂,等于这个数的p次幂的倒数.
am÷an=am-n(a≠0,m,n都是正整数).
这样,对于任何正整数m,n,都有
例1 计算:
(1)106÷102 (2)23÷25
(3)5m÷5m-1 (4)an÷an+1(a≠0)
典型例题
解:(1)106÷102
(2)23÷25
=106-2
=104
=23-5
=2-2
(3)5m÷5m-1
=5m-(m-1)
=5
(4)an÷an+1
=an-(n+1)
=a-1
【当堂检测】
1.判断.
(1)a4÷a3=a7
(2)a2÷a5=a10
(3)(-b)4÷(-b)2=-b2
(4)(-1)0=-1
×
×
×
a4÷a3=a
a2÷a5=a-3
(-b)4÷(-b)2=b4÷b2=b2
×
(-1)0=1
2.计算.
【当堂检测】
(2)m5÷m2
(4)(x2)2·x÷x5
(1)x7÷x3
(1)原式=x7-3=x4
(2)原式=m5-2=m3
(3)原式=(xy)7-6=xy
(4)原式=x5-5=1
(3)(xy)7÷(xy)6
解:
例2 计算:
(1)a8÷a2÷a3 (2)(-x)9÷(-x)5÷(-x)3
解:(1)原式=a8-2÷a3
=a8-2-3
总结:由同底数幂相除的法则,我们可以推出:
am÷an÷aq=am-n-q(a≠0,m,n,q都是正整数).
(2)原式=(-x)9-5÷(-x)3
=a3
=(-x)9-5-3
=-x
典型例题
3.计算.
【当堂检测】
(1)(x-y)9÷(y-x)6÷(x-y)
(1)原式=(x-y)9-6-1 =(x-y)2
(2)原式=(xy)7-6-3 =(xy)-2=
(2)(xy)7÷(xy)6÷(xy)3
解:
例3.已知:xa=4,xb=9,求:(1)xa-b;(2)x3a-2b.
分析:因为xa÷xb=xa-b,所以xa-b=xa÷xb.
解:
(2)因为xa=4,xb=9,
总结:可逆用同底数幂相除的法则进行求值:
am-n=am÷an(a≠0,m,n都是正整数).
(1)因为xa=4,xb=9;
所以xa-b=xa÷xb
所以x3a-2b=x3a÷x2b
所以x3a=(xa)3=64,x2b=(xb)2=81;
典型例题
4.如果3m=10,3n=5,那么3m-n的值为多少?
【当堂检测】
解:当3m=10,3n=5,
原式=3m÷3n
=10÷5
=2
故3m-n的值2.
典型例题
例4.计算:
(1)x3 x5-(2x4)2+x10÷x2.
(2)(x-y)9÷(y-x)6·(x-y)
解:
(2)原式=(x-y)9÷(x-y)6·(x-y)
(1)原式=x8-4x8+x8
注意:计算时要先将互为相反数的底数转化为相同的底数.
=-2x8
=(x-y)4
5.计算:
(1)22020×0.52018÷22
(2)(a3)2÷(a4·a2)
【当堂检测】
解:
(1)原式=22×(22018×0.52018)÷22
=1
(2)原式=a6÷a6
=a6-6
=1
=22×(2×0.5)2018÷22
四、课堂总结
同底数幂的除法
法则
am÷an=am-n (a≠0,m,n都是正整数)
零指数幂和负指数幂
同底数幂相除,底数不变,指数相减
a0=1 (a≠0)
(a≠0,p是正整数)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
