9.2 三角形的内角和外角 第2课时 课件 (共20张PPT)2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 9.2 三角形的内角和外角 第2课时 课件 (共20张PPT)2023-2024学年初中数学冀教版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
第九章 三角形
9.2 三角形的内角和外角
第2课时
1.知道三角形外角的概念,会识别三角形的外角;
2.掌握三角形的外角的有关性质,并能运用这些性质解决简单的问题.(重点)
一、学习目标
二、新课导入
数一数:下面的图形中你能数出多少个角?
A
B
C
D
一共数出4个角,它们分别是∠A,∠C,∠ABC,∠CBD
我们知道∠A,∠C,∠ABC是△ABC的三个内角,那∠CBD和△ABC又
有什么关系呢?
三、概念剖析
A
B
C
D
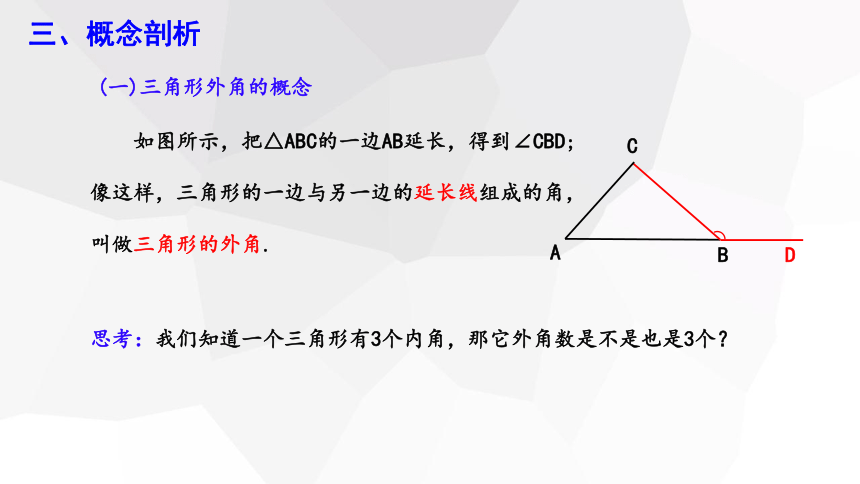
如图所示,把△ABC的一边AB延长,得到∠CBD;
像这样,三角形的一边与另一边的延长线组成的角,
叫做三角形的外角.
思考:我们知道一个三角形有3个内角,那它外角数是不是也是3个?
(一)三角形外角的概念
三、概念剖析
画一画:先画一个任意三角形,根据三角的定义画出该三角形全部外角.
(
(
(
(
(
(
A
B
C
1
2
3
4
5
6
A
B
如图所示,我们发现
每一个三角形都有6个外角;
每一个顶点相对应的外角都有2个,
且这2个角为对顶角.
三、概念剖析
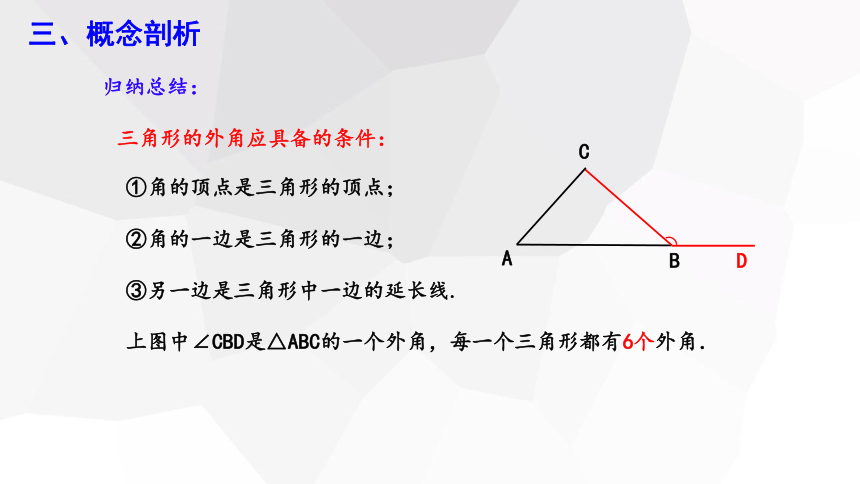
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
上图中∠CBD是△ABC的一个外角,每一个三角形都有6个外角.
A
B
C
D
归纳总结:
三、概念剖析
(二)三角形外角的性质
那么三角形的外角与三角形的内角有哪些关系呢?
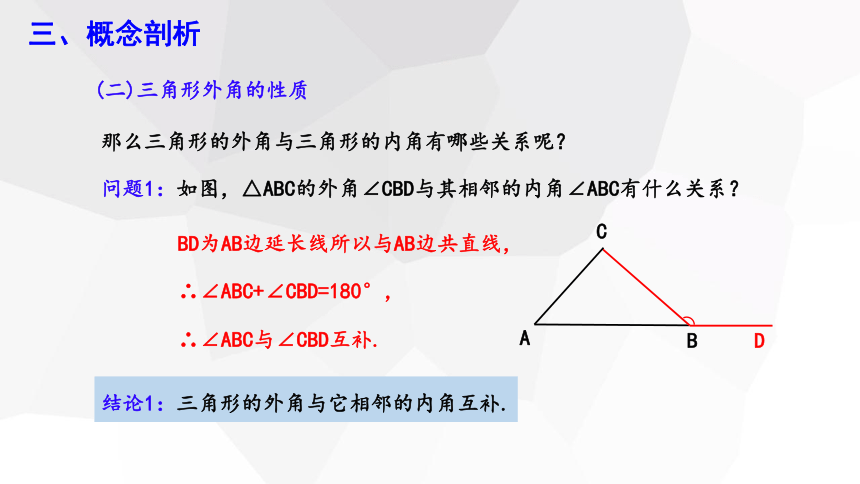
问题1:如图,△ABC的外角∠CBD与其相邻的内角∠ABC有什么关系?
A
B
C
D
BD为AB边延长线所以与AB边共直线,
∴∠ABC+∠CBD=180°,
∴∠ABC与∠CBD互补.
结论1:三角形的外角与它相邻的内角互补.
三、概念剖析
问题2:如图,△ABC的外角∠CBD与其不相邻的两个内角∠A和∠C有什么关系?
A
B
C
D
由问题1可知∠ABC+∠CBD=180°,
∴∠CBD=180°-∠ABC,
在△ABC中∠A+∠C+∠ABC=180°(三角形内角和定理),
∴∠A+∠C=180°-∠ABC,
故∠CBD=∠A+∠C (等量代换).
结论2:三角形的一个外角等于与它不相邻的两个内角的和.
三、概念剖析
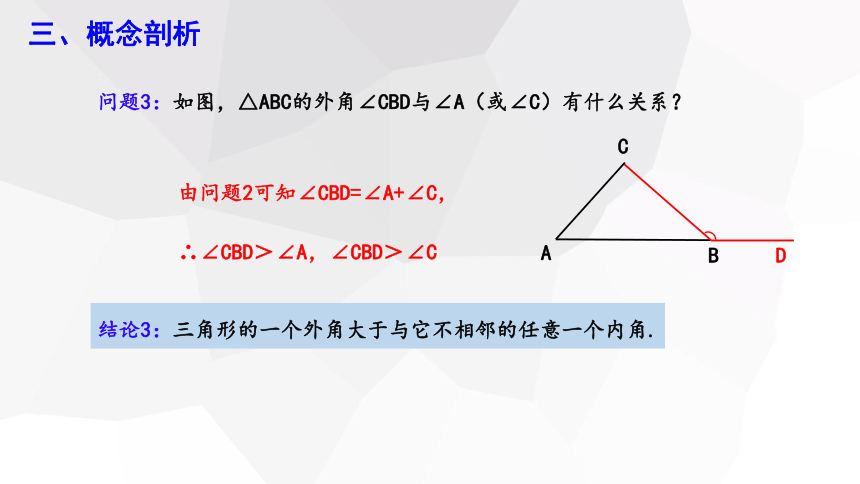
问题3:如图,△ABC的外角∠CBD与∠A(或∠C)有什么关系?
A
B
C
D
由问题2可知∠CBD=∠A+∠C,
∴∠CBD>∠A,∠CBD>∠C
结论3:三角形的一个外角大于与它不相邻的任意一个内角.
问题:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
三个内角都是锐角的三角形
有一个内角是直角的三角形
有一个内角是钝角的三角形
三、概念剖析
(三)三角形外角的分类
锐角三角形
直角三角形
钝角三角形
按是否有边相等分
按内角大小分
三角形
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
三、概念剖析
典型例题
例1.如图, ∠BAE、∠CBF、∠ACD是△ABC的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:
∠BAE= ∠2+ ∠3,∠CBF= ∠1+ ∠3,∠ACD= ∠1+ ∠2
(三角形的一个外角等于与它不相邻的两个内角的和),
∵∠1+ ∠2+ ∠3=180 °,(三角形内角和定理)
∴∠BAE+ ∠CBF+ ∠ACD=2(∠1+ ∠2+ ∠3)=360 °.
典型例题
(
(
(
总结:如图,三角形的三个不同位置的外角和等于360°
(
(
(
【当堂检测】
1.如果三角形三个外角度数之比是3:4:5,则此三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
B
例2. 如图,∠BCD=92°,∠A=27°,∠BED=44°,求
(1) ∠B的度数;
A
C
D
E
B
解:(1) 在△ABC中,
∵∠BCD=∠A+∠B(三角形的一个外角等于与它不相邻的两个内角的和),
∠BCD=92°,∠A=27°,(已知)
∴∠B=∠BCD-∠A=92°-27°=65°;
典型例题
F
(2) 在△BEF中,
∵ ∠BFD=∠B+∠BED(三角形的一个外角等于与它不相邻的两个内角的和),
∠BED=44°(已知),∠B=65°,(已知)
∴∠BFD=44°+65°=109°.
(2) ∠BFD的度数;
典型例题
A
C
D
E
B
F
典型例题
总结:在三角形组合图形问题中,条件中只给出某些角的度数,让我们求一个角的度数.这类题型一般解法就是利用三角形内角和定理以及三角形外角的性质,找出已知角的度数和需要求的角的度数之间的关系.分析时一般先从需要求的角与其他角的关系出发,一步步把所有未知量用已知量表示.
2.如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,(三角形的一个外角等于与它不相邻的两个内角的和)
∵ ∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,(三角形的一个外角等于与它不相邻的两个内角的和)
∵ ∠ABD=28°, ∠BEC=60°,
∴ ∠BFC=88°.
解:
B
C
A
F
E
D
【当堂检测】
3.点O是△ABC内一点,∠A=85°,∠1=15°,∠2=40°,求∠BOC的度数.
【当堂检测】
解:如图,延长BO交AC于D,
D
(
(
A
1
2
0
C
B
答:∠BOC为140°.
∴∠BOC=∠CDO+∠2=140°,(三角形的一个外角等于与它不相邻的 两个内角的和)
又∵∠2=40°,
∴∠CDO=∠1+∠A=100°,(三角形的一个外 角等于与它不相邻的两个内角的和)
∵∠A=85°,∠1=15°,
四、课堂总结
1.三角形的外角的定义:
三角形的一边与另一边的延长线组成的角
2.三角形的外角的性质:
(1)三角形的一个外角等于与它不相邻的两个内角的和
(2)三角形的外角与它相邻的内角互补
3.三角形的外角和:
三角形的三个不同位置的外角和等于360°
4.三角形按内角大小分:
锐角三角形、直角三角形、钝角三角形
第九章 三角形
9.2 三角形的内角和外角
第2课时
1.知道三角形外角的概念,会识别三角形的外角;
2.掌握三角形的外角的有关性质,并能运用这些性质解决简单的问题.(重点)
一、学习目标
二、新课导入
数一数:下面的图形中你能数出多少个角?
A
B
C
D
一共数出4个角,它们分别是∠A,∠C,∠ABC,∠CBD
我们知道∠A,∠C,∠ABC是△ABC的三个内角,那∠CBD和△ABC又
有什么关系呢?
三、概念剖析
A
B
C
D
如图所示,把△ABC的一边AB延长,得到∠CBD;
像这样,三角形的一边与另一边的延长线组成的角,
叫做三角形的外角.
思考:我们知道一个三角形有3个内角,那它外角数是不是也是3个?
(一)三角形外角的概念
三、概念剖析
画一画:先画一个任意三角形,根据三角的定义画出该三角形全部外角.
(
(
(
(
(
(
A
B
C
1
2
3
4
5
6
A
B
如图所示,我们发现
每一个三角形都有6个外角;
每一个顶点相对应的外角都有2个,
且这2个角为对顶角.
三、概念剖析
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
上图中∠CBD是△ABC的一个外角,每一个三角形都有6个外角.
A
B
C
D
归纳总结:
三、概念剖析
(二)三角形外角的性质
那么三角形的外角与三角形的内角有哪些关系呢?
问题1:如图,△ABC的外角∠CBD与其相邻的内角∠ABC有什么关系?
A
B
C
D
BD为AB边延长线所以与AB边共直线,
∴∠ABC+∠CBD=180°,
∴∠ABC与∠CBD互补.
结论1:三角形的外角与它相邻的内角互补.
三、概念剖析
问题2:如图,△ABC的外角∠CBD与其不相邻的两个内角∠A和∠C有什么关系?
A
B
C
D
由问题1可知∠ABC+∠CBD=180°,
∴∠CBD=180°-∠ABC,
在△ABC中∠A+∠C+∠ABC=180°(三角形内角和定理),
∴∠A+∠C=180°-∠ABC,
故∠CBD=∠A+∠C (等量代换).
结论2:三角形的一个外角等于与它不相邻的两个内角的和.
三、概念剖析
问题3:如图,△ABC的外角∠CBD与∠A(或∠C)有什么关系?
A
B
C
D
由问题2可知∠CBD=∠A+∠C,
∴∠CBD>∠A,∠CBD>∠C
结论3:三角形的一个外角大于与它不相邻的任意一个内角.
问题:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
三个内角都是锐角的三角形
有一个内角是直角的三角形
有一个内角是钝角的三角形
三、概念剖析
(三)三角形外角的分类
锐角三角形
直角三角形
钝角三角形
按是否有边相等分
按内角大小分
三角形
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
三、概念剖析
典型例题
例1.如图, ∠BAE、∠CBF、∠ACD是△ABC的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:
∠BAE= ∠2+ ∠3,∠CBF= ∠1+ ∠3,∠ACD= ∠1+ ∠2
(三角形的一个外角等于与它不相邻的两个内角的和),
∵∠1+ ∠2+ ∠3=180 °,(三角形内角和定理)
∴∠BAE+ ∠CBF+ ∠ACD=2(∠1+ ∠2+ ∠3)=360 °.
典型例题
(
(
(
总结:如图,三角形的三个不同位置的外角和等于360°
(
(
(
【当堂检测】
1.如果三角形三个外角度数之比是3:4:5,则此三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
B
例2. 如图,∠BCD=92°,∠A=27°,∠BED=44°,求
(1) ∠B的度数;
A
C
D
E
B
解:(1) 在△ABC中,
∵∠BCD=∠A+∠B(三角形的一个外角等于与它不相邻的两个内角的和),
∠BCD=92°,∠A=27°,(已知)
∴∠B=∠BCD-∠A=92°-27°=65°;
典型例题
F
(2) 在△BEF中,
∵ ∠BFD=∠B+∠BED(三角形的一个外角等于与它不相邻的两个内角的和),
∠BED=44°(已知),∠B=65°,(已知)
∴∠BFD=44°+65°=109°.
(2) ∠BFD的度数;
典型例题
A
C
D
E
B
F
典型例题
总结:在三角形组合图形问题中,条件中只给出某些角的度数,让我们求一个角的度数.这类题型一般解法就是利用三角形内角和定理以及三角形外角的性质,找出已知角的度数和需要求的角的度数之间的关系.分析时一般先从需要求的角与其他角的关系出发,一步步把所有未知量用已知量表示.
2.如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,(三角形的一个外角等于与它不相邻的两个内角的和)
∵ ∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,(三角形的一个外角等于与它不相邻的两个内角的和)
∵ ∠ABD=28°, ∠BEC=60°,
∴ ∠BFC=88°.
解:
B
C
A
F
E
D
【当堂检测】
3.点O是△ABC内一点,∠A=85°,∠1=15°,∠2=40°,求∠BOC的度数.
【当堂检测】
解:如图,延长BO交AC于D,
D
(
(
A
1
2
0
C
B
答:∠BOC为140°.
∴∠BOC=∠CDO+∠2=140°,(三角形的一个外角等于与它不相邻的 两个内角的和)
又∵∠2=40°,
∴∠CDO=∠1+∠A=100°,(三角形的一个外 角等于与它不相邻的两个内角的和)
∵∠A=85°,∠1=15°,
四、课堂总结
1.三角形的外角的定义:
三角形的一边与另一边的延长线组成的角
2.三角形的外角的性质:
(1)三角形的一个外角等于与它不相邻的两个内角的和
(2)三角形的外角与它相邻的内角互补
3.三角形的外角和:
三角形的三个不同位置的外角和等于360°
4.三角形按内角大小分:
锐角三角形、直角三角形、钝角三角形
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
