9.3 三角形的角平分线、中线和高 课件(共16张PPT) 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 9.3 三角形的角平分线、中线和高 课件(共16张PPT) 2023-2024学年初中数学冀教版七年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:49:14 | ||
图片预览





文档简介
(共16张PPT)
第九章 三角形
9.3 三角形的角平分线、中线和高
1.知道三角形的高、中线与角平分线的概念,能熟练地画出任意三角形的高、中线、与角平分线;
一、学习目标
2.能应用三角形的高、中线与角平分线的性质进行简单计算.
二、新课导入
旧知回顾:
2.线段中点的定义:
把一条线段分成两条相等的线段的点.
A
B
O
如图所示,若AO=B0,则0点为线段AB中点.
1.角的平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线,
叫这个角的平分线.
如图所示,射线OB为∠A0C的角平分线,
其中∠A0B=∠B0C.
二、新课导入
旧知回顾:
3.垂线的定义:
两直线相交所成的四个角中,有一个角是直角时,就说这
两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
A
B
C
D
90°
如图所示,直线CD为直线AB的垂线.
三、概念剖析
(一)三角形的角平分线
如图,在△ABC中作∠A的平分线交BC于D点,
注意:△ABC的角平分线有三条,都是线段;角的平分线是射线.
A
B
C
D
三角形一个内角的平分线与它的对边相交,这个角的顶点与交点间的线段叫做三角形的角平分线.
可得∠BAD =∠CAD,
三、概念剖析
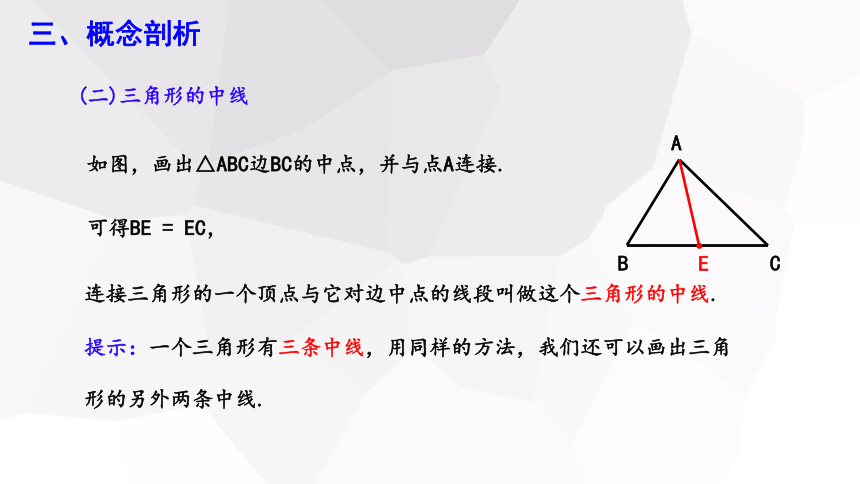
(二)三角形的中线
如图,画出△ABC边BC的中点,并与点A连接.
A
B
C
E
提示:一个三角形有三条中线,用同样的方法,我们还可以画出三角形的另外两条中线.
连接三角形的一个顶点与它对边中点的线段叫做这个三角形的中线.
可得BE = EC,
三、概念剖析
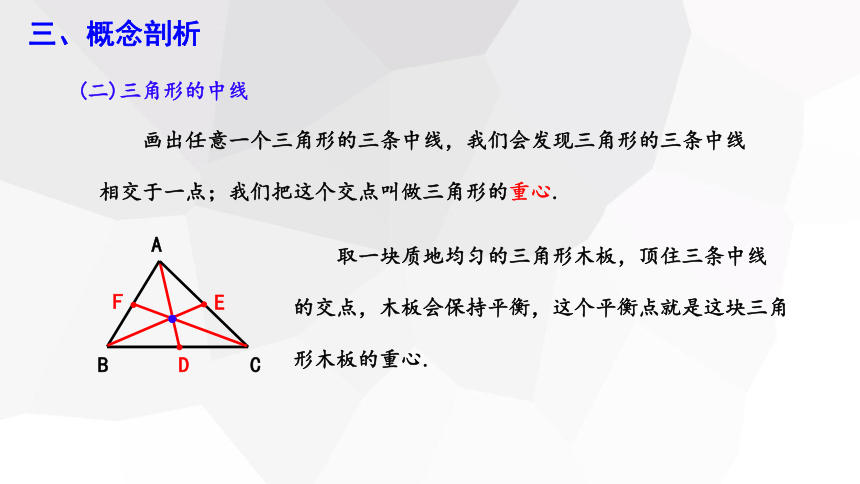
画出任意一个三角形的三条中线,我们会发现三角形的三条中线
相交于一点;我们把这个交点叫做三角形的重心.
(二)三角形的中线
A
B
C
D
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
F
E
三、概念剖析
我们已经学过直线外的一个点该直线的垂线,而且只能画出1条垂线.
那如果在△ABC中,我们也可以过顶点A画出对边BC的垂线,如图:
(三)三角形的高
A
B
C
F
直线AF与直线BC的交点为F,
我们把三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,简称三角形的高.
一个三角形有三条高,用上面一样的方法,我们还可以画出三角形
的另外两条高.
注意:标明垂直的记号和垂足的字母.
例1:如图,(1)(2)(3)中的三个三角形?画出各个△ABC的三条高,并观察概括它们的特点?
典型例题
(1)
(2)
(3)
解:锐角三角形的三条高交于同一点;三条高和三条高的交点都在三角形的内部.
钝角三角形的三条高不相交于一点;三条高所在直线交于一点.
直角三角形的三条高交于直角顶点;有两条高为直角边.
O
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
F
1.画出下列三个角的角平分线,观察概括它们的特点?
【当堂检测】
解:三角形的三条角平分线相交于一点,交点在三角形的内部.
例2.如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小.
典型例题
解: ∵ AD是△ABC的高,
∴∠ADC=90°,
∵ ∠ADC+∠C+∠DAC=180°,
∴ ∠DAC=180°-(∠ADC+∠C)
=180°-90°-40°=50°,
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE= ∠BAC=41°,
∴∠DAE=∠DAC-∠CAE=50°-41°= 9°.
A
B
C
D
E
分析:根据三角形高,角平分线的定义,找出各角度间的隐藏关系,结合三角形的内角和定义可求出角度.
【当堂检测】
2.如图,在△ABC中,∠ABC=62°,BD是角平分线,CE是高,BD与CE交于点O,求∠BOC的大小.
解: ∵ CE是△ABC的高,
∴∠BEC=90°,
∵ ∠BEC+∠ABC+∠BCE=180°,
∴ ∠BCE=180°-(∠BEC+∠ABC)
=180°-90°-62°=28°,
∵BD是△ABC的角平分线,且∠ABC=62°,
∴∠ABD=∠OBC= ∠ABC=31°,
∴∠BOC=180°-∠OBC-∠BCE=121°.
A
B
C
O
E
D
解:△ABD的面积等于△ADC面积.
典型例题
A
B
C
D
例3:在三角形ABC中,AD为BC边上的中线,则△ABD与△ADC面积有什么关系?为什么?
E
总结:三角形的中线平分该三角形的面积.
∴S△ABD=S△ADC .
又∵AD为BC边上的中线,
根据三角形的面积公式可得:S△ABD= (BD×AE),S△ADC= (CD×AE);
如图作△ABC的BC边上的垂线,交BC于点E,
∴D为BC上的中点,BD=CD;
【当堂检测】
3.在△ABC中,CD是中线,已知BC-AC=6cm, △DBC的周长为20cm,求△ADC
的周长.
解:∵CD是△ABC的中线,
△ABC中线CD把原三角形分成的两个三角形的周长差就是BC与AC的差.
A
D
B
C
∴ △ADC的周长=20-6=14(cm).
又∵ △DBC的周长为20cm,
∴ △DBC与△ADC的周长差是6cm;
∴(BC+BD+CD)-(AC+AD+CD)=6cm,
∵BC-AC=6cm,
∴BD=AD ,
4.如图,在△ABC中,∠ABC=90°,把△ABC沿直线AB对折,使点C落在点C'的位置,则线段AB .
(1)是△ACC'的中线.
(2)是△ACC'的高.
(3)是△ACC'的角平分线.
【当堂检测】
(1)(2)(3)
A
B
C
C'
四、课堂总结
三角形
高:三角形的一个顶点到它对边所在直线的垂线段叫做三角形
的高线,简称三角形的高.
角平分线:三角形一个内角的平分线与它的对边相交,这个角
的顶点与交点间的线段叫做三角形的角平分线.
中线:连接三角形的一个顶点与它对边中点的线段叫做这个三
角形的中线.
第九章 三角形
9.3 三角形的角平分线、中线和高
1.知道三角形的高、中线与角平分线的概念,能熟练地画出任意三角形的高、中线、与角平分线;
一、学习目标
2.能应用三角形的高、中线与角平分线的性质进行简单计算.
二、新课导入
旧知回顾:
2.线段中点的定义:
把一条线段分成两条相等的线段的点.
A
B
O
如图所示,若AO=B0,则0点为线段AB中点.
1.角的平分线:
从一个角的顶点出发,把这个角分成相等的两个角的射线,
叫这个角的平分线.
如图所示,射线OB为∠A0C的角平分线,
其中∠A0B=∠B0C.
二、新课导入
旧知回顾:
3.垂线的定义:
两直线相交所成的四个角中,有一个角是直角时,就说这
两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
A
B
C
D
90°
如图所示,直线CD为直线AB的垂线.
三、概念剖析
(一)三角形的角平分线
如图,在△ABC中作∠A的平分线交BC于D点,
注意:△ABC的角平分线有三条,都是线段;角的平分线是射线.
A
B
C
D
三角形一个内角的平分线与它的对边相交,这个角的顶点与交点间的线段叫做三角形的角平分线.
可得∠BAD =∠CAD,
三、概念剖析
(二)三角形的中线
如图,画出△ABC边BC的中点,并与点A连接.
A
B
C
E
提示:一个三角形有三条中线,用同样的方法,我们还可以画出三角形的另外两条中线.
连接三角形的一个顶点与它对边中点的线段叫做这个三角形的中线.
可得BE = EC,
三、概念剖析
画出任意一个三角形的三条中线,我们会发现三角形的三条中线
相交于一点;我们把这个交点叫做三角形的重心.
(二)三角形的中线
A
B
C
D
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
F
E
三、概念剖析
我们已经学过直线外的一个点该直线的垂线,而且只能画出1条垂线.
那如果在△ABC中,我们也可以过顶点A画出对边BC的垂线,如图:
(三)三角形的高
A
B
C
F
直线AF与直线BC的交点为F,
我们把三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,简称三角形的高.
一个三角形有三条高,用上面一样的方法,我们还可以画出三角形
的另外两条高.
注意:标明垂直的记号和垂足的字母.
例1:如图,(1)(2)(3)中的三个三角形?画出各个△ABC的三条高,并观察概括它们的特点?
典型例题
(1)
(2)
(3)
解:锐角三角形的三条高交于同一点;三条高和三条高的交点都在三角形的内部.
钝角三角形的三条高不相交于一点;三条高所在直线交于一点.
直角三角形的三条高交于直角顶点;有两条高为直角边.
O
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
F
1.画出下列三个角的角平分线,观察概括它们的特点?
【当堂检测】
解:三角形的三条角平分线相交于一点,交点在三角形的内部.
例2.如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小.
典型例题
解: ∵ AD是△ABC的高,
∴∠ADC=90°,
∵ ∠ADC+∠C+∠DAC=180°,
∴ ∠DAC=180°-(∠ADC+∠C)
=180°-90°-40°=50°,
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠CAE= ∠BAC=41°,
∴∠DAE=∠DAC-∠CAE=50°-41°= 9°.
A
B
C
D
E
分析:根据三角形高,角平分线的定义,找出各角度间的隐藏关系,结合三角形的内角和定义可求出角度.
【当堂检测】
2.如图,在△ABC中,∠ABC=62°,BD是角平分线,CE是高,BD与CE交于点O,求∠BOC的大小.
解: ∵ CE是△ABC的高,
∴∠BEC=90°,
∵ ∠BEC+∠ABC+∠BCE=180°,
∴ ∠BCE=180°-(∠BEC+∠ABC)
=180°-90°-62°=28°,
∵BD是△ABC的角平分线,且∠ABC=62°,
∴∠ABD=∠OBC= ∠ABC=31°,
∴∠BOC=180°-∠OBC-∠BCE=121°.
A
B
C
O
E
D
解:△ABD的面积等于△ADC面积.
典型例题
A
B
C
D
例3:在三角形ABC中,AD为BC边上的中线,则△ABD与△ADC面积有什么关系?为什么?
E
总结:三角形的中线平分该三角形的面积.
∴S△ABD=S△ADC .
又∵AD为BC边上的中线,
根据三角形的面积公式可得:S△ABD= (BD×AE),S△ADC= (CD×AE);
如图作△ABC的BC边上的垂线,交BC于点E,
∴D为BC上的中点,BD=CD;
【当堂检测】
3.在△ABC中,CD是中线,已知BC-AC=6cm, △DBC的周长为20cm,求△ADC
的周长.
解:∵CD是△ABC的中线,
△ABC中线CD把原三角形分成的两个三角形的周长差就是BC与AC的差.
A
D
B
C
∴ △ADC的周长=20-6=14(cm).
又∵ △DBC的周长为20cm,
∴ △DBC与△ADC的周长差是6cm;
∴(BC+BD+CD)-(AC+AD+CD)=6cm,
∵BC-AC=6cm,
∴BD=AD ,
4.如图,在△ABC中,∠ABC=90°,把△ABC沿直线AB对折,使点C落在点C'的位置,则线段AB .
(1)是△ACC'的中线.
(2)是△ACC'的高.
(3)是△ACC'的角平分线.
【当堂检测】
(1)(2)(3)
A
B
C
C'
四、课堂总结
三角形
高:三角形的一个顶点到它对边所在直线的垂线段叫做三角形
的高线,简称三角形的高.
角平分线:三角形一个内角的平分线与它的对边相交,这个角
的顶点与交点间的线段叫做三角形的角平分线.
中线:连接三角形的一个顶点与它对边中点的线段叫做这个三
角形的中线.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
