11.2 提公因式法 课件(共19张PPT) 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 11.2 提公因式法 课件(共19张PPT) 2023-2024学年初中数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 625.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:56:17 | ||
图片预览






文档简介
(共19张PPT)
第 十一 章 因式分解
11.2 提公因式法
一、学习目标
1.知道公因式及提公因式法的概念;
2.能确定多项式的公因式,并运用提公因式法将多项式分解因式.
(重点)
二、新课导入
知识回顾
填一填
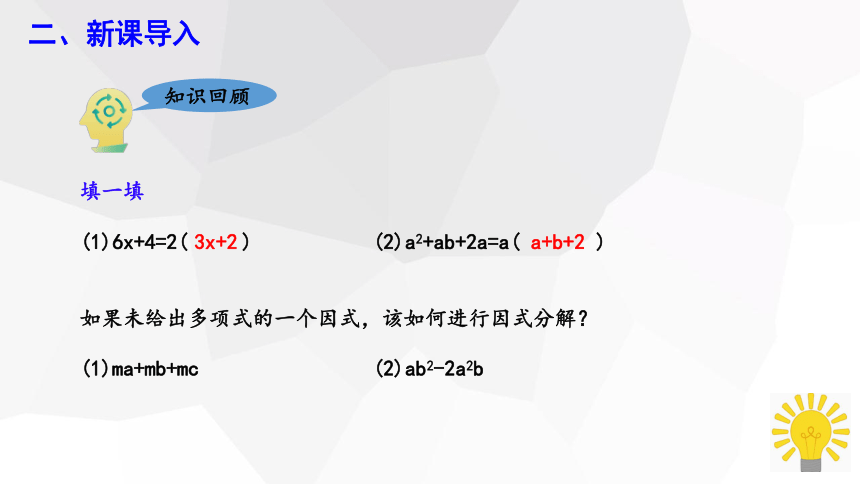
(1)6x+4=2( ) (2)a2+ab+2a=a( )
3x+2
a+b+2
如果未给出多项式的一个因式,该如何进行因式分解?
(1)ma+mb+mc (2)ab2-2a2b
三、概念剖析
1.多项式ma+mb+mc有几项?每一项的因式都有哪些?这些项中有没有公共
的因式?若有,是哪个?
思考
2.多项式ab2-2a2b的两项中,有没有公共的因式?若有,是哪些?
三、概念剖析
实际上,有:
多项式 项 各项的公共因式
ma+mb+mc ma,mb,mc m
ab2-2a2b ab2,-2a2b a,b,ab
一般地,多项式的各项都含有的因式,叫做这个多项式各项的公因式,
简称多项式的公因式.
例如,ma+mb+mc的公因式就是m.
三、概念剖析
逆用乘法对加法的分配律,可以把公因式写在括号外边,作为积的一个因式,
写成下面的形式:
ma+mb+mc=m(a+b+c),
ab2-2a2b=ab(b-2a).
这种将多项式分解因式的方法,叫做提公因式法.
四、典型例题
例1.写出下列多项式因式分解过程中需要提取的公因式:
(1)3a2y - 3ay + 6y;
(2)-27a2b3 + 36a3b2 + 9a2b;
(3)(2a + b)(2a-3b)-8a(2a + b).
3y
-9a2b
2a+b
思考:式(2)中-9ab也是多项式的公因式,为什么不写-9ab?
四、典型例题
一看系数:若各项系数都是整数,应提取各项系数的最大公约数;
归纳总结
找准公因式要“五看”:
二看字母:公因式的字母是各项相同的字母;
8a+4b
4
公因式
18x-12y+6m
6
公因式
ab+ac
a
公因式
abc+abd+abp
ab
公因式
四、典型例题
五看首项符号:若多项式中首项含有负号,则公因式符号为负.
四看整体:如果多项式中含有相同的多项式,应将其看作整体,不要拆开;
三看字母的次数:各相同字母的指数取次数最低的;
ab2+a2b
ab
公因式
ab2c3+a2bc2
abc2
公因式
a(a+c)+b(a+c)
a+c
公因式
-ab2+abc
-ab
公因式
【当堂检测】
1.写出下列多项式因式分解过程中需要提取的公因式:
(1)6x-9x2;
(2)abc+2a;
(3)abc-ab2+2ab;
(4)2x2y+4xy2-6xy.
3x
a
ab
2xy
四、典型例题
例2.因式分解:
(1)-4m3+16m2-4m; (2)2a(b+c)-3(b+c).
解:(1)原式=(-4m)·m2 +(-4m)·(-4m)+(-4m)·1
(2)2a(b+c)-3(b+c)
= -4m(m2 -4m+1).
将b+c看作一个整体“提”出来
=(b+c)(2a-3).
小提示:将结果做整式的乘法运算,可检查因式分解是否正确.
四、典型例题
反思:将多项式4a2b3-3ab2分解因式,小戴的过程如下,你觉得正确吗?
解:4a2b3-3ab2
=ab(4ab2-3b)
分析:结果中的因式4ab2-3b含有公因式b,所以该因式还能继续分解.
因此,小戴的过程不正确.
还能继续分解吗?
改正:4a2b3-3ab2
=ab2(4ab-3)
四、典型例题
分解因式时需注意的事项:
(1)用提公因式法分解因式时,要注意分解彻底;
(2)当某项恰好是公因式时,提取公因式后要在该项的位置上补上“1”;
归纳总结
【当堂检测】
2.把下列各式分解因式.
(1)5a2-7ab (2)4am2-8amn+4a
解:
(2)原式=4a·m2-4a·2mn+4a·1,
=a(5a-7b).
(1)原式=a·5a-a·7b
=4a(m2-2mn+1).
(3)6(m-n)3-12(m-n)2
(3)原式=6(m-n)2·(m-n) - 6(m-n)2·2,
=6(m-n)2(m-n-2).
【当堂检测】
(4)x(a-x)(a-y)-y(x-a)(y-a).
原式=x(a-x)(a-y)-y(a-x)(a-y)
=(a-x)(a-y)(x-y).
提示:含有(b-a)3,(b-a)2等形式的多项式,可将(b-a)3,(b-a)2化成
-(a-b)3,(a-b)2的形式,即指数是奇数时要改变符号,指数是偶数
时不改变符号,简言之:奇变偶不变.
四、典型例题
例3.计算:
29×20.20+72×20.20+13×20.20-14×20.20.
分析:首先提取公因式20.20,进而利用有理数的运算法则求解即可.
解:
原式=20.20×(29+72+13-14)
=20.20×100
=2020.
【当堂检测】
3.用简便方法计算:
(1)1012-101;
(2)2020×2019-2020×2018+2020.
解:
(1)原式=101×(101-1)=101×100=10100;
(2)原式=2020×(2019-2018+1)=2020×2=4040.
五、课堂总结
公因式的概念以及公因式的确定方法
(1)一般地,多项式的各项都含有的因式,叫做这个多项式各项的________.
(2)确定公因式:当多项式的各项系数都是整数时,公因式的系数应取各项
系数的___________,字母应取各项______的字母,且_______字母的指数取
次数________的.
公因式
最大公约数
相同
相同
最低
五、课堂总结
提公因式法分解因式
一般地,如果多项式含有公因式,逆用乘法对加法的________律,可以把
这个公因式写在括号外面,作为积的一个因式,将多项式写成整式乘积的
形式.这种将多项式分解因式的方法,叫做提公因式法.
分配
第 十一 章 因式分解
11.2 提公因式法
一、学习目标
1.知道公因式及提公因式法的概念;
2.能确定多项式的公因式,并运用提公因式法将多项式分解因式.
(重点)
二、新课导入
知识回顾
填一填
(1)6x+4=2( ) (2)a2+ab+2a=a( )
3x+2
a+b+2
如果未给出多项式的一个因式,该如何进行因式分解?
(1)ma+mb+mc (2)ab2-2a2b
三、概念剖析
1.多项式ma+mb+mc有几项?每一项的因式都有哪些?这些项中有没有公共
的因式?若有,是哪个?
思考
2.多项式ab2-2a2b的两项中,有没有公共的因式?若有,是哪些?
三、概念剖析
实际上,有:
多项式 项 各项的公共因式
ma+mb+mc ma,mb,mc m
ab2-2a2b ab2,-2a2b a,b,ab
一般地,多项式的各项都含有的因式,叫做这个多项式各项的公因式,
简称多项式的公因式.
例如,ma+mb+mc的公因式就是m.
三、概念剖析
逆用乘法对加法的分配律,可以把公因式写在括号外边,作为积的一个因式,
写成下面的形式:
ma+mb+mc=m(a+b+c),
ab2-2a2b=ab(b-2a).
这种将多项式分解因式的方法,叫做提公因式法.
四、典型例题
例1.写出下列多项式因式分解过程中需要提取的公因式:
(1)3a2y - 3ay + 6y;
(2)-27a2b3 + 36a3b2 + 9a2b;
(3)(2a + b)(2a-3b)-8a(2a + b).
3y
-9a2b
2a+b
思考:式(2)中-9ab也是多项式的公因式,为什么不写-9ab?
四、典型例题
一看系数:若各项系数都是整数,应提取各项系数的最大公约数;
归纳总结
找准公因式要“五看”:
二看字母:公因式的字母是各项相同的字母;
8a+4b
4
公因式
18x-12y+6m
6
公因式
ab+ac
a
公因式
abc+abd+abp
ab
公因式
四、典型例题
五看首项符号:若多项式中首项含有负号,则公因式符号为负.
四看整体:如果多项式中含有相同的多项式,应将其看作整体,不要拆开;
三看字母的次数:各相同字母的指数取次数最低的;
ab2+a2b
ab
公因式
ab2c3+a2bc2
abc2
公因式
a(a+c)+b(a+c)
a+c
公因式
-ab2+abc
-ab
公因式
【当堂检测】
1.写出下列多项式因式分解过程中需要提取的公因式:
(1)6x-9x2;
(2)abc+2a;
(3)abc-ab2+2ab;
(4)2x2y+4xy2-6xy.
3x
a
ab
2xy
四、典型例题
例2.因式分解:
(1)-4m3+16m2-4m; (2)2a(b+c)-3(b+c).
解:(1)原式=(-4m)·m2 +(-4m)·(-4m)+(-4m)·1
(2)2a(b+c)-3(b+c)
= -4m(m2 -4m+1).
将b+c看作一个整体“提”出来
=(b+c)(2a-3).
小提示:将结果做整式的乘法运算,可检查因式分解是否正确.
四、典型例题
反思:将多项式4a2b3-3ab2分解因式,小戴的过程如下,你觉得正确吗?
解:4a2b3-3ab2
=ab(4ab2-3b)
分析:结果中的因式4ab2-3b含有公因式b,所以该因式还能继续分解.
因此,小戴的过程不正确.
还能继续分解吗?
改正:4a2b3-3ab2
=ab2(4ab-3)
四、典型例题
分解因式时需注意的事项:
(1)用提公因式法分解因式时,要注意分解彻底;
(2)当某项恰好是公因式时,提取公因式后要在该项的位置上补上“1”;
归纳总结
【当堂检测】
2.把下列各式分解因式.
(1)5a2-7ab (2)4am2-8amn+4a
解:
(2)原式=4a·m2-4a·2mn+4a·1,
=a(5a-7b).
(1)原式=a·5a-a·7b
=4a(m2-2mn+1).
(3)6(m-n)3-12(m-n)2
(3)原式=6(m-n)2·(m-n) - 6(m-n)2·2,
=6(m-n)2(m-n-2).
【当堂检测】
(4)x(a-x)(a-y)-y(x-a)(y-a).
原式=x(a-x)(a-y)-y(a-x)(a-y)
=(a-x)(a-y)(x-y).
提示:含有(b-a)3,(b-a)2等形式的多项式,可将(b-a)3,(b-a)2化成
-(a-b)3,(a-b)2的形式,即指数是奇数时要改变符号,指数是偶数
时不改变符号,简言之:奇变偶不变.
四、典型例题
例3.计算:
29×20.20+72×20.20+13×20.20-14×20.20.
分析:首先提取公因式20.20,进而利用有理数的运算法则求解即可.
解:
原式=20.20×(29+72+13-14)
=20.20×100
=2020.
【当堂检测】
3.用简便方法计算:
(1)1012-101;
(2)2020×2019-2020×2018+2020.
解:
(1)原式=101×(101-1)=101×100=10100;
(2)原式=2020×(2019-2018+1)=2020×2=4040.
五、课堂总结
公因式的概念以及公因式的确定方法
(1)一般地,多项式的各项都含有的因式,叫做这个多项式各项的________.
(2)确定公因式:当多项式的各项系数都是整数时,公因式的系数应取各项
系数的___________,字母应取各项______的字母,且_______字母的指数取
次数________的.
公因式
最大公约数
相同
相同
最低
五、课堂总结
提公因式法分解因式
一般地,如果多项式含有公因式,逆用乘法对加法的________律,可以把
这个公因式写在括号外面,作为积的一个因式,将多项式写成整式乘积的
形式.这种将多项式分解因式的方法,叫做提公因式法.
分配
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
