第九章 三角形复习课 课件 21张PPT 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 第九章 三角形复习课 课件 21张PPT 2023-2024学年初中数学冀教版七年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 923.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 11:01:14 | ||
图片预览





文档简介
(共21张PPT)
第九章 三角形
复习课
3.知道三角形的高、中线、角平分线概念,会画三角形的高、中线、角平分线并运用性质计算.
一、学习目标
1.掌握三角形的三边关系,并能运用三角形三边关系解决有关的问题;
2.能应用三角形外角和内角的性质解决问题,了解三角形分类;
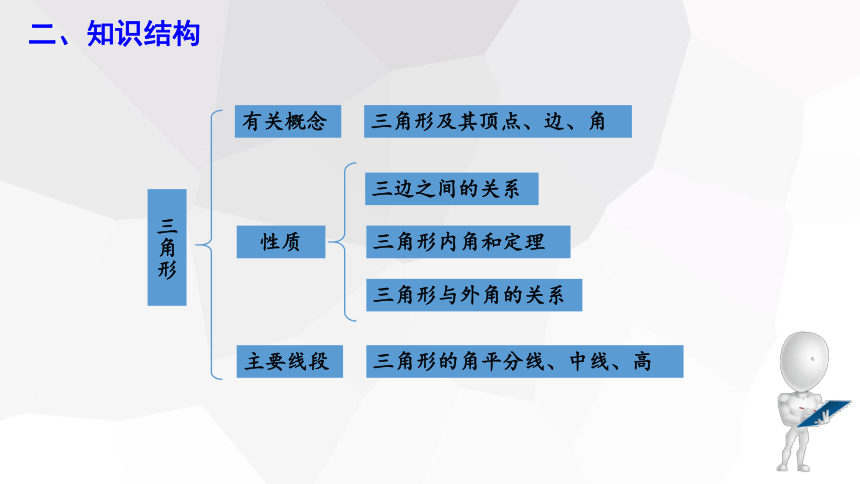
二、知识结构
三角形
性质
三角形及其顶点、边、角
三边之间的关系
三角形内角和定理
三角形的角平分线、中线、高
三角形与外角的关系
有关概念
主要线段
三、知识梳理
三角形:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫 做三角形.
边:组成三角形的三条线段AB,BC,AC叫做三角形的边,
内角:∠A,∠B,∠C叫做三角形的内角.
顶角:点A,B,C叫做三角形的顶点,
1.三角形的有关概念
外角:三角形的一边与另一边的延长线组成的角,
叫做三角形的外角.
A
B
C
边
内角
顶点
D
外角
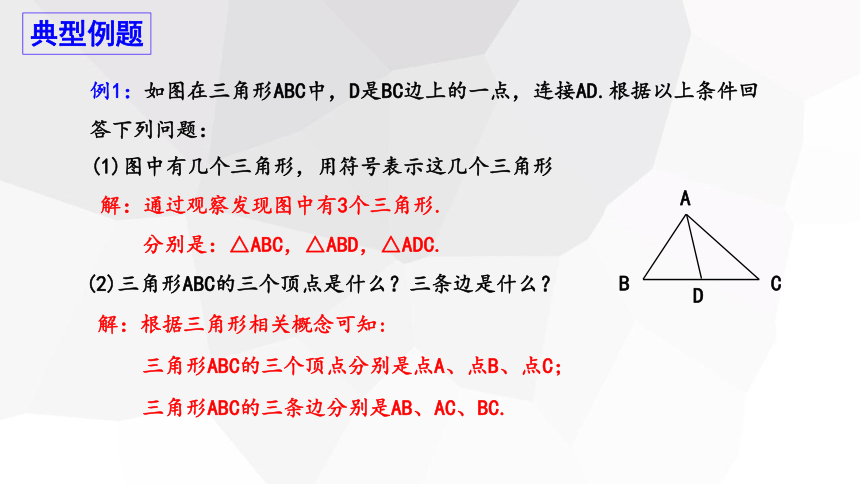
例1:如图在三角形ABC中,D是BC边上的一点,连接AD.根据以上条件回
答下列问题:
典型例题
A
B
C
D
(1)图中有几个三角形,用符号表示这几个三角形
解:通过观察发现图中有3个三角形.
(2)三角形ABC的三个顶点是什么?三条边是什么?
解:根据三角形相关概念可知:
分别是:△ABC,△ABD,△ADC.
三角形ABC的三个顶点分别是点A、点B、点C;
三角形ABC的三条边分别是AB、AC、BC.
典型例题
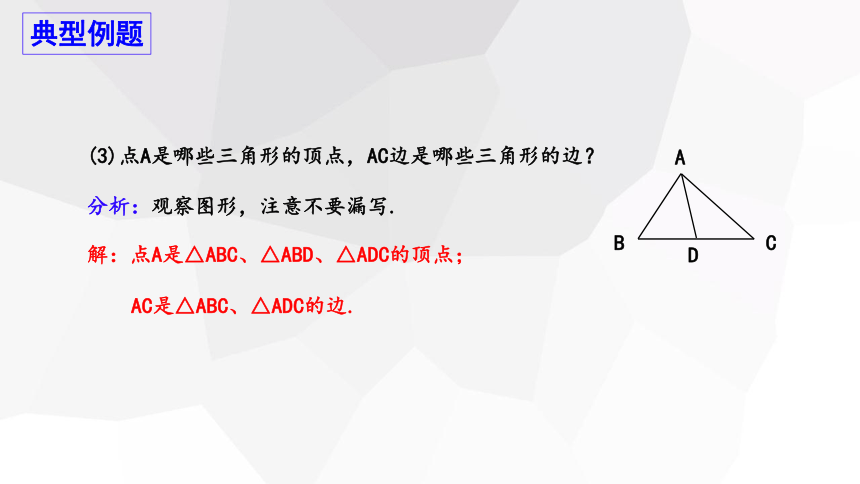
解:点A是△ABC、△ABD、△ADC的顶点;
(3)点A是哪些三角形的顶点,AC边是哪些三角形的边?
分析:观察图形,注意不要漏写.
AC是△ABC、△ADC的边.
A
B
C
D
【当堂检测】
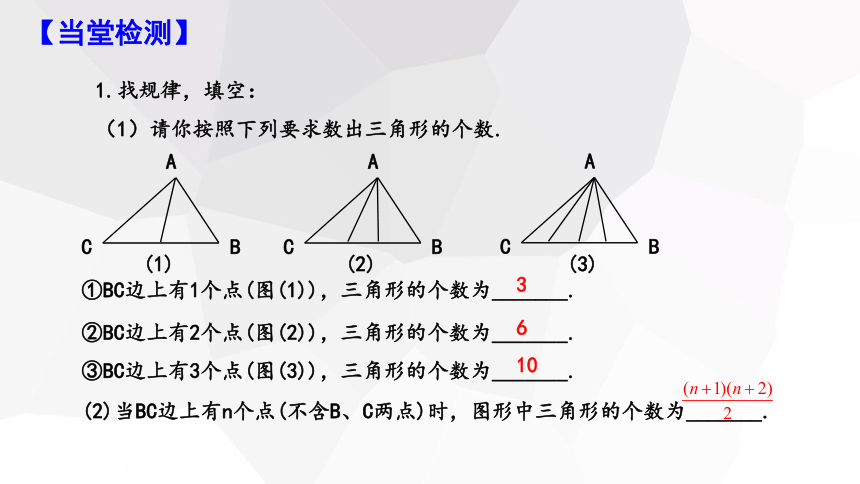
1.找规律,填空:
(1)请你按照下列要求数出三角形的个数.
3
A
B
C
(1)
A
B
C
(2)
A
B
C
(3)
①BC边上有1个点(图(1)),三角形的个数为_______.
②BC边上有2个点(图(2)),三角形的个数为_______.
③BC边上有3个点(图(3)),三角形的个数为_______.
(2)当BC边上有n个点(不含B、C两点)时,图形中三角形的个数为_______.
6
10
三、知识梳理
三角形任意两边的和大于第三边,三角形两边的差小于第三边.
2.三角形三边之间的关系
锐角三角形
直角三角形
钝角三角形
按是否有边相等分类
按内角大小分类
三角形
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
3.三角形的分类
例2:已知两条线段的长分别是3cm、8cm ,要想拼成一个三角形,且第三条线段a的长为奇数,问第三条线段应取多长?
典型例题
分析:根据三角形的三边关系满足8-3得 8-3∴ 5 解:由三角形两边之和大于第三边,两边之差小于第三边,
又∵第三边长为奇数,
∴第三条边长为 7cm或9cm.
【当堂检测】
2.三角形的三条边长都是整数,周长为11,有一边为4,这个三角形可能的最大边长是多少?请说明理由.
4+6+1、4+5+2、4+4+3
∵三角形两边之和大于第三边,
解:3个整数之和为11,可能的组合有:
∴4+6+1排除,
那么最大边长为5.
三角形内角和定理:三角形的内角和等于180 °.
三角形的一个外角等于与它不相邻的两个内角之和.
三角形的一个外角大于与它不相邻的任意一个内角.
三角形的外角和等于360°.
三、知识梳理
4.三角形角的性质
例3:“三角形的外角和等于360°”说明理由.
典型例题
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:∵∠BAE+∠1=180°,
∴∠BAE+∠CBF+∠ACD=540°-180°=360°.
∵△ABC中,∠1+∠2+∠3=180°,(三角形内角和定理)
∴∠BAE+∠CBF+∠ACD=540°-(∠1+∠2+∠3),
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3
=180°×3=540°.
∠CBF+∠2=180°,∠ACD+∠3=180°.
【当堂检测】
3.△ABC的一个内角为40°,∠A=∠B.你能说出△ABC的外角分别是多少度吗?
∠A=∠B=40°,
∠C=180°-∠A-∠B=100°,
解:当∠A=40°时,
当∠C=40°时,
∠A+∠B=180°-40°=140°,
∠A=∠B=70°.
此时三个外角分别为80°、140°、140°;
此时三个外角分别为110°、110°、140°.
三、知识梳理
连接三角形的一个顶点与它对边中点的线段叫做这个三角形的中线.
三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段做三角形的角平分线.
三角形的三条中线相交于一点;我们把这个交点叫做三角形的重心.
5.三角形中主要的线段
我们把三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,简称三角形的高.
三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
(1)过点A画出它的高、过点B作出其中线、过点C作出其角平分线.
例4.如图△ABC的三个顶点分别为A、B、C.
A
B
C
A
B
C
A
B
C
D
AD⊥BC
A0=C0
∠ACE=∠BCE
0
E
典型例题
(2)BO为△ABC中线,已知BC-AB=4cm, △B0C的周长为16cm,求△A0B的周长.
A
B
C
0
解:∵BO是△ABC的中线,
典型例题
∴ △A0B的周长=16-4=12(cm).
又∵ △B0C的周长为16cm,
∴ △B0C与△A0B的周长差是6cm;
∴(BC+BO+CO)-(AB+A0+B0)=6cm,
∵BC-AB=6cm,
∴A0=C0 .
4.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=________.
【当堂检测】
解析:∵点D是AC的中点,∴AD= AC,
∴S△ABD= S△ABC= ×12=6.
∴S△ABE= S△ABC= ×12=4.
2
∴S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)
=S△ADF-S△BEF,
∵EC=2BE,S△ABC=12,
∵S△ABC=12,
5.如图,在△ABC中,AD是BC边上的高线,CE是一条角平分线,且相交
于点P.已知∠APE=55°,∠AEP=80°,∠B的度数是多少?
A
B
C
D
E
P
解:∵AD⊥BC,
【当堂检测】
故∠B的度数是为45°.
∴∠B=80°-35°=45°,
∵∠AEP=∠B+∠ECB,
∴∠PCD=90°-55°=35°,
∵∠CPD=∠APE=55°,
∴∠PDC=90°,
【当堂检测】
6.如图,△ABC中,∠C=45°,∠A=55°,BE是△ABC角平分线,点D在AB
上,且DE∥BC,求∠DEB的度数.
A
B
C
D
E
解:∵∠C=45°,∠A=55°,
∴∠DEB=∠CBE=40°.
∵DE∥BC,
∴∠CBE=40°,
又∵BE平分∠ABC,
∴∠ABC=80°,
7.如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,
已知∠D=29°,则∠1的度数为多少?
【当堂检测】
A
B
C
D
1
(
∴∠1=180°-∠BAC-∠ABC=180°-90°-58°=32°.
∵∠BAC=90°,
∴∠ABC=2∠ABD=58°,
又∵BD平分∠ABC,
∴∠ABD=∠D=29°(两直线平行,内错角相等)
解:∵CD∥AB,∠D=29°,
四、课堂总结
三角形
与三角形有关的线段
三角形内角和:180°
三角形外角和:360°
三角形的边:三边关系定理
高线
中线:把三角形面积平分
角平分线
与三角形有关的角
内角与外角关系
三角形的分类
第九章 三角形
复习课
3.知道三角形的高、中线、角平分线概念,会画三角形的高、中线、角平分线并运用性质计算.
一、学习目标
1.掌握三角形的三边关系,并能运用三角形三边关系解决有关的问题;
2.能应用三角形外角和内角的性质解决问题,了解三角形分类;
二、知识结构
三角形
性质
三角形及其顶点、边、角
三边之间的关系
三角形内角和定理
三角形的角平分线、中线、高
三角形与外角的关系
有关概念
主要线段
三、知识梳理
三角形:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫 做三角形.
边:组成三角形的三条线段AB,BC,AC叫做三角形的边,
内角:∠A,∠B,∠C叫做三角形的内角.
顶角:点A,B,C叫做三角形的顶点,
1.三角形的有关概念
外角:三角形的一边与另一边的延长线组成的角,
叫做三角形的外角.
A
B
C
边
内角
顶点
D
外角
例1:如图在三角形ABC中,D是BC边上的一点,连接AD.根据以上条件回
答下列问题:
典型例题
A
B
C
D
(1)图中有几个三角形,用符号表示这几个三角形
解:通过观察发现图中有3个三角形.
(2)三角形ABC的三个顶点是什么?三条边是什么?
解:根据三角形相关概念可知:
分别是:△ABC,△ABD,△ADC.
三角形ABC的三个顶点分别是点A、点B、点C;
三角形ABC的三条边分别是AB、AC、BC.
典型例题
解:点A是△ABC、△ABD、△ADC的顶点;
(3)点A是哪些三角形的顶点,AC边是哪些三角形的边?
分析:观察图形,注意不要漏写.
AC是△ABC、△ADC的边.
A
B
C
D
【当堂检测】
1.找规律,填空:
(1)请你按照下列要求数出三角形的个数.
3
A
B
C
(1)
A
B
C
(2)
A
B
C
(3)
①BC边上有1个点(图(1)),三角形的个数为_______.
②BC边上有2个点(图(2)),三角形的个数为_______.
③BC边上有3个点(图(3)),三角形的个数为_______.
(2)当BC边上有n个点(不含B、C两点)时,图形中三角形的个数为_______.
6
10
三、知识梳理
三角形任意两边的和大于第三边,三角形两边的差小于第三边.
2.三角形三边之间的关系
锐角三角形
直角三角形
钝角三角形
按是否有边相等分类
按内角大小分类
三角形
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
3.三角形的分类
例2:已知两条线段的长分别是3cm、8cm ,要想拼成一个三角形,且第三条线段a的长为奇数,问第三条线段应取多长?
典型例题
分析:根据三角形的三边关系满足8-3
又∵第三边长为奇数,
∴第三条边长为 7cm或9cm.
【当堂检测】
2.三角形的三条边长都是整数,周长为11,有一边为4,这个三角形可能的最大边长是多少?请说明理由.
4+6+1、4+5+2、4+4+3
∵三角形两边之和大于第三边,
解:3个整数之和为11,可能的组合有:
∴4+6+1排除,
那么最大边长为5.
三角形内角和定理:三角形的内角和等于180 °.
三角形的一个外角等于与它不相邻的两个内角之和.
三角形的一个外角大于与它不相邻的任意一个内角.
三角形的外角和等于360°.
三、知识梳理
4.三角形角的性质
例3:“三角形的外角和等于360°”说明理由.
典型例题
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:∵∠BAE+∠1=180°,
∴∠BAE+∠CBF+∠ACD=540°-180°=360°.
∵△ABC中,∠1+∠2+∠3=180°,(三角形内角和定理)
∴∠BAE+∠CBF+∠ACD=540°-(∠1+∠2+∠3),
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3
=180°×3=540°.
∠CBF+∠2=180°,∠ACD+∠3=180°.
【当堂检测】
3.△ABC的一个内角为40°,∠A=∠B.你能说出△ABC的外角分别是多少度吗?
∠A=∠B=40°,
∠C=180°-∠A-∠B=100°,
解:当∠A=40°时,
当∠C=40°时,
∠A+∠B=180°-40°=140°,
∠A=∠B=70°.
此时三个外角分别为80°、140°、140°;
此时三个外角分别为110°、110°、140°.
三、知识梳理
连接三角形的一个顶点与它对边中点的线段叫做这个三角形的中线.
三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段做三角形的角平分线.
三角形的三条中线相交于一点;我们把这个交点叫做三角形的重心.
5.三角形中主要的线段
我们把三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,简称三角形的高.
三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
(1)过点A画出它的高、过点B作出其中线、过点C作出其角平分线.
例4.如图△ABC的三个顶点分别为A、B、C.
A
B
C
A
B
C
A
B
C
D
AD⊥BC
A0=C0
∠ACE=∠BCE
0
E
典型例题
(2)BO为△ABC中线,已知BC-AB=4cm, △B0C的周长为16cm,求△A0B的周长.
A
B
C
0
解:∵BO是△ABC的中线,
典型例题
∴ △A0B的周长=16-4=12(cm).
又∵ △B0C的周长为16cm,
∴ △B0C与△A0B的周长差是6cm;
∴(BC+BO+CO)-(AB+A0+B0)=6cm,
∵BC-AB=6cm,
∴A0=C0 .
4.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=________.
【当堂检测】
解析:∵点D是AC的中点,∴AD= AC,
∴S△ABD= S△ABC= ×12=6.
∴S△ABE= S△ABC= ×12=4.
2
∴S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)
=S△ADF-S△BEF,
∵EC=2BE,S△ABC=12,
∵S△ABC=12,
5.如图,在△ABC中,AD是BC边上的高线,CE是一条角平分线,且相交
于点P.已知∠APE=55°,∠AEP=80°,∠B的度数是多少?
A
B
C
D
E
P
解:∵AD⊥BC,
【当堂检测】
故∠B的度数是为45°.
∴∠B=80°-35°=45°,
∵∠AEP=∠B+∠ECB,
∴∠PCD=90°-55°=35°,
∵∠CPD=∠APE=55°,
∴∠PDC=90°,
【当堂检测】
6.如图,△ABC中,∠C=45°,∠A=55°,BE是△ABC角平分线,点D在AB
上,且DE∥BC,求∠DEB的度数.
A
B
C
D
E
解:∵∠C=45°,∠A=55°,
∴∠DEB=∠CBE=40°.
∵DE∥BC,
∴∠CBE=40°,
又∵BE平分∠ABC,
∴∠ABC=80°,
7.如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,
已知∠D=29°,则∠1的度数为多少?
【当堂检测】
A
B
C
D
1
(
∴∠1=180°-∠BAC-∠ABC=180°-90°-58°=32°.
∵∠BAC=90°,
∴∠ABC=2∠ABD=58°,
又∵BD平分∠ABC,
∴∠ABD=∠D=29°(两直线平行,内错角相等)
解:∵CD∥AB,∠D=29°,
四、课堂总结
三角形
与三角形有关的线段
三角形内角和:180°
三角形外角和:360°
三角形的边:三边关系定理
高线
中线:把三角形面积平分
角平分线
与三角形有关的角
内角与外角关系
三角形的分类
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
