第七章 相交线与平行线 复习课课件 23张PPT 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 第七章 相交线与平行线 复习课课件 23张PPT 2023-2024学年初中数学冀教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 163.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
第七章 相交线与平行线
复习课
一、学习目标
1.理解命题的概念,会说明一个命题是真命题,会用举反例的方法说明一个命题是假命题.
2.掌握对顶角、垂线的概念和性质.
3.理解同位角、内错角、同旁内角的概念.
4.掌握平行线的概念、性质,会判断两条直线是否平行,能综合运用平行线的性质和判定解决问题.
5.知道平移的概念、性质.
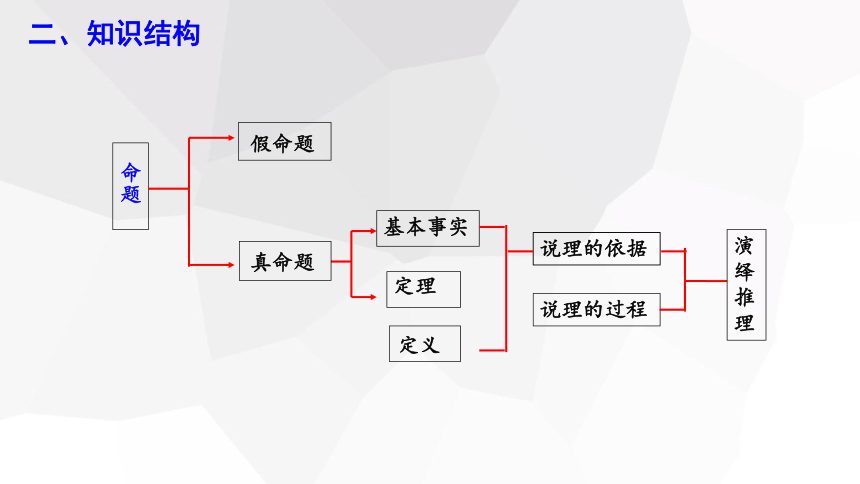
二、知识结构
基本事实
说理的依据
定理
说理的过程
假命题
真命题
命题
定义
演绎推理
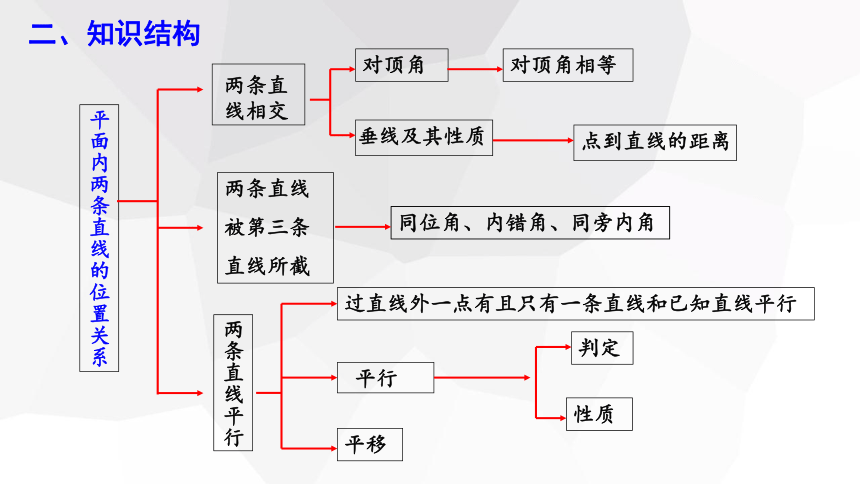
二、知识结构
对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条直线相交
两条直线
被第三条
直线所截
平面内两条直线的位置关系
同位角、内错角、同旁内角
两条直线平行
平行
平移
判定
性质
过直线外一点有且只有一条直线和已知直线平行
三、知识回顾
知识点一 命题
1.能够进行肯定或者否定判断的语句叫做命题.
2. 命题有真有假,其中正确的命题叫做真命题;错误的命题叫做假命题.
3. 要说明一个命题是假命题,只要举出一个符合命题条件,不符合命题结论的例子就可以,像这样的例子称为反例.
4.经过实践验证的真命题称为基本事实.
5.经过演绎推理得到的重要的真命题叫做定理.
(1)两条直线相交所构成的四个角中,有公共顶点但没有公共边的两个角是对顶角.如图
1
2
3
4
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角.
2.对顶角性质:对顶角相等.
两个特征:(1) 具有公共顶点;(2) 角的两边互为反向延长线.
∠1和∠2, ∠3和∠4是对顶角.
1. 对顶角:
知识点二 对顶角
三、知识回顾
1. 垂线的性质:
(1)过一点有且只有一条直线与已知直线垂直.
知识点三 垂线
(2)直线外一点与直线上各点连结的所有线段中,垂线段最短.
简称:垂线段最短.
2.点到直线的距离:
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
三、知识回顾
知识点四 同位角、内错角、同旁内角
同位角的位置特征是: (1)在截线的同旁,(2)被截两直线的同方向.
内错角的位置特征是: (1)在截线的两旁,(2)在被截两直线之间.
同旁内角的位置特征是: (1)在截线的同旁,(2)在被截两直线之间.
三、知识回顾
知识点五 平行线
1.平行线的概念:
在同一平面内,不相交的两条直线叫做平行线.
2. 平行线的基本性质:
(2) 两条平行线之间的距离处处相等.
(1)经过直线外一点,有且只有一条直线与已知直线平行.
三、知识回顾
知识点六 平行线的判定
1.三种角判定(3种方法):
2.在同一平面内,垂直于同一条直线的两条直线平行.
(3)同旁内角互补,两直线平行.
(2)内错角相等,两直线平行;
(1)同位角相等,两直线平行;
三、知识回顾
知识点七 平行线的性质
(1)两直线平行,同位角相等;
(3)两直线平行,同旁内角互补;
(2)两直线平行,内错角相等;
(4)平行于同一条直线的两条直线平行.
三、知识回顾
知识点八 平移
1.平移的概念
(1)平移的两个图形形状和大小完全相同
(2)对应线段平行(或在同一直线上)且相等,对应角相等;
(3)各对应点所连线段平行(或在同一直线上)且相等;
在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动称为平移.
2.平移的性质
三、知识回顾
典型例题
例1.如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么AD=CB”是真命题.
A
C
D
B
理由:∵ AC=DB(已知),
∴ AC+CD=DB+CD(等式的性质),
∴ AD=CB(线段和的定义).
∴ 是真命题.
【当堂检测】
1.如图,AC⊥BC,垂足为点C,∠BCD是∠B的余角.试说明:∠ACD=∠B.
理由:因为AC⊥BC(已知),
所以∠BCD是∠ACD的余角( )
所以∠ACB=90°( )
又因为∠BCD是∠B的余角( 已知 )
所以∠ACD=∠B( )
C
B
D
垂直的定义
余角的定义
等量代换
A
典型例题
例2.如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
解:
∵AB⊥CD,(已知)
∵∠AOE=65°,(已知)
∴∠AOC=90°.(垂直的定义)
∴∠COE=25°(两角差的性质)
又∵∠COE=∠DOF (对顶角相等)
∴∠DOF=25°.(等量代换)
【当堂检测】
2.如图.直线AB、CD相交于点O,OE⊥AB于O,OB平分∠ DOF,∠DOE=50°,求∠AOC、 ∠ EOF、 ∠ COF的度数.
解:∵AB⊥OE (已知)
∵∠DOE= 50°,(已知)
∴ ∠EOB=90°,(垂直的定义)
∴ ∠DOB=40°,(余角的定义)
∴∠AOC= ∠DOB=40°,(对顶角相等)
又∵OB平分∠DOF,(已知)
∠COF=∠COD-∠DOF =180°-80°=100°(两角差的定义)
∴∠BOF= ∠DOB=40°(角平分线性质)
∴∠EOF= ∠EOB+ ∠BOF =90°+40°=130°(两角和的定义)
例3. 如图所示,能表示点到直线(线段)的距离的线段有几条.
解:从图中可以看到共有5条,
B
C
D
A
总结:点到直线的距离容易和两点之间的距离相混淆.当图形复杂不容易分析出是哪条线段时,准确掌握概念,抓住垂直这个关键点,认真分析图形是关键.
C到AD的垂线段CD.
B到AD的垂线段BD,
A到BC的垂线段AD,
典型例题
B到AC的垂线段BA,
C到AB的垂线段CA,
【当堂检测】
3.如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是 cm.
4.8
6
8
例4.如图所示,直线a、b被c、d所截,且c⊥a,c⊥b.∠1与∠2相等吗?
说明理由.
解:∠1与∠2 的度数相等.
理由:∵直线a、b 被c 、d所截,且 c⊥a, c⊥b,
∴ ∠3=∠4=90 (垂直的定义)
∴ a//b(同位角相等,两直线平行)
∴ ∠5=∠2(两直线平行,同位角相等)
∵ ∠5=∠1(对顶角相等)
∴ ∠2=∠1(等量代换)
a
b
c
d
典型例题
【当堂检测】
A
B
C
D
E
F
1
2
3
4.填空:
(1)∵∠A=____, (已知)
AC∥ED ,( )
(2) ∵AB ∥______, (已知)
∠2= ∠4,( )
4
5
(3) ___ ∥___, (已知)
∠B= ∠3. ( )
∠4
同位角相等,两直线平行.
DF
两直线平行, 内错角相等.
AB
DF
两直线平行, 同位角相等.
∴
∴
∴
∵
例5.如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是( )
D
典型例题
【当堂检测】
5.如图所示,△DEF经过平移得到△ABC, 那么∠C的对应角和ED的对应边分别是( )
A.∠F;AC
B.∠BOD;BA
C.∠F;BA
D.∠BOD;AC
C
四、课堂总结
相交线
对顶角相等
过一点有且只有一条直线与已知直线垂直
过直线外一点有且只有一条直线与已知直线平行
平行线
同位角相等,两直线平行
平行线的判定
平行线的性质
两直线平行,同旁内角互补
相交线与平行线
同旁内角互补,两直线平行
内错角相等,两直线平行
两直线平行,同位角相等
两直线平行,内错角相等
平移
第七章 相交线与平行线
复习课
一、学习目标
1.理解命题的概念,会说明一个命题是真命题,会用举反例的方法说明一个命题是假命题.
2.掌握对顶角、垂线的概念和性质.
3.理解同位角、内错角、同旁内角的概念.
4.掌握平行线的概念、性质,会判断两条直线是否平行,能综合运用平行线的性质和判定解决问题.
5.知道平移的概念、性质.
二、知识结构
基本事实
说理的依据
定理
说理的过程
假命题
真命题
命题
定义
演绎推理
二、知识结构
对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条直线相交
两条直线
被第三条
直线所截
平面内两条直线的位置关系
同位角、内错角、同旁内角
两条直线平行
平行
平移
判定
性质
过直线外一点有且只有一条直线和已知直线平行
三、知识回顾
知识点一 命题
1.能够进行肯定或者否定判断的语句叫做命题.
2. 命题有真有假,其中正确的命题叫做真命题;错误的命题叫做假命题.
3. 要说明一个命题是假命题,只要举出一个符合命题条件,不符合命题结论的例子就可以,像这样的例子称为反例.
4.经过实践验证的真命题称为基本事实.
5.经过演绎推理得到的重要的真命题叫做定理.
(1)两条直线相交所构成的四个角中,有公共顶点但没有公共边的两个角是对顶角.如图
1
2
3
4
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角.
2.对顶角性质:对顶角相等.
两个特征:(1) 具有公共顶点;(2) 角的两边互为反向延长线.
∠1和∠2, ∠3和∠4是对顶角.
1. 对顶角:
知识点二 对顶角
三、知识回顾
1. 垂线的性质:
(1)过一点有且只有一条直线与已知直线垂直.
知识点三 垂线
(2)直线外一点与直线上各点连结的所有线段中,垂线段最短.
简称:垂线段最短.
2.点到直线的距离:
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
三、知识回顾
知识点四 同位角、内错角、同旁内角
同位角的位置特征是: (1)在截线的同旁,(2)被截两直线的同方向.
内错角的位置特征是: (1)在截线的两旁,(2)在被截两直线之间.
同旁内角的位置特征是: (1)在截线的同旁,(2)在被截两直线之间.
三、知识回顾
知识点五 平行线
1.平行线的概念:
在同一平面内,不相交的两条直线叫做平行线.
2. 平行线的基本性质:
(2) 两条平行线之间的距离处处相等.
(1)经过直线外一点,有且只有一条直线与已知直线平行.
三、知识回顾
知识点六 平行线的判定
1.三种角判定(3种方法):
2.在同一平面内,垂直于同一条直线的两条直线平行.
(3)同旁内角互补,两直线平行.
(2)内错角相等,两直线平行;
(1)同位角相等,两直线平行;
三、知识回顾
知识点七 平行线的性质
(1)两直线平行,同位角相等;
(3)两直线平行,同旁内角互补;
(2)两直线平行,内错角相等;
(4)平行于同一条直线的两条直线平行.
三、知识回顾
知识点八 平移
1.平移的概念
(1)平移的两个图形形状和大小完全相同
(2)对应线段平行(或在同一直线上)且相等,对应角相等;
(3)各对应点所连线段平行(或在同一直线上)且相等;
在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动称为平移.
2.平移的性质
三、知识回顾
典型例题
例1.如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么AD=CB”是真命题.
A
C
D
B
理由:∵ AC=DB(已知),
∴ AC+CD=DB+CD(等式的性质),
∴ AD=CB(线段和的定义).
∴ 是真命题.
【当堂检测】
1.如图,AC⊥BC,垂足为点C,∠BCD是∠B的余角.试说明:∠ACD=∠B.
理由:因为AC⊥BC(已知),
所以∠BCD是∠ACD的余角( )
所以∠ACB=90°( )
又因为∠BCD是∠B的余角( 已知 )
所以∠ACD=∠B( )
C
B
D
垂直的定义
余角的定义
等量代换
A
典型例题
例2.如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
解:
∵AB⊥CD,(已知)
∵∠AOE=65°,(已知)
∴∠AOC=90°.(垂直的定义)
∴∠COE=25°(两角差的性质)
又∵∠COE=∠DOF (对顶角相等)
∴∠DOF=25°.(等量代换)
【当堂检测】
2.如图.直线AB、CD相交于点O,OE⊥AB于O,OB平分∠ DOF,∠DOE=50°,求∠AOC、 ∠ EOF、 ∠ COF的度数.
解:∵AB⊥OE (已知)
∵∠DOE= 50°,(已知)
∴ ∠EOB=90°,(垂直的定义)
∴ ∠DOB=40°,(余角的定义)
∴∠AOC= ∠DOB=40°,(对顶角相等)
又∵OB平分∠DOF,(已知)
∠COF=∠COD-∠DOF =180°-80°=100°(两角差的定义)
∴∠BOF= ∠DOB=40°(角平分线性质)
∴∠EOF= ∠EOB+ ∠BOF =90°+40°=130°(两角和的定义)
例3. 如图所示,能表示点到直线(线段)的距离的线段有几条.
解:从图中可以看到共有5条,
B
C
D
A
总结:点到直线的距离容易和两点之间的距离相混淆.当图形复杂不容易分析出是哪条线段时,准确掌握概念,抓住垂直这个关键点,认真分析图形是关键.
C到AD的垂线段CD.
B到AD的垂线段BD,
A到BC的垂线段AD,
典型例题
B到AC的垂线段BA,
C到AB的垂线段CA,
【当堂检测】
3.如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是 cm.
4.8
6
8
例4.如图所示,直线a、b被c、d所截,且c⊥a,c⊥b.∠1与∠2相等吗?
说明理由.
解:∠1与∠2 的度数相等.
理由:∵直线a、b 被c 、d所截,且 c⊥a, c⊥b,
∴ ∠3=∠4=90 (垂直的定义)
∴ a//b(同位角相等,两直线平行)
∴ ∠5=∠2(两直线平行,同位角相等)
∵ ∠5=∠1(对顶角相等)
∴ ∠2=∠1(等量代换)
a
b
c
d
典型例题
【当堂检测】
A
B
C
D
E
F
1
2
3
4.填空:
(1)∵∠A=____, (已知)
AC∥ED ,( )
(2) ∵AB ∥______, (已知)
∠2= ∠4,( )
4
5
(3) ___ ∥___, (已知)
∠B= ∠3. ( )
∠4
同位角相等,两直线平行.
DF
两直线平行, 内错角相等.
AB
DF
两直线平行, 同位角相等.
∴
∴
∴
∵
例5.如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是( )
D
典型例题
【当堂检测】
5.如图所示,△DEF经过平移得到△ABC, 那么∠C的对应角和ED的对应边分别是( )
A.∠F;AC
B.∠BOD;BA
C.∠F;BA
D.∠BOD;AC
C
四、课堂总结
相交线
对顶角相等
过一点有且只有一条直线与已知直线垂直
过直线外一点有且只有一条直线与已知直线平行
平行线
同位角相等,两直线平行
平行线的判定
平行线的性质
两直线平行,同旁内角互补
相交线与平行线
同旁内角互补,两直线平行
内错角相等,两直线平行
两直线平行,同位角相等
两直线平行,内错角相等
平移
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
