第十一章 因式分解复习课课件 30张PPT 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 第十一章 因式分解复习课课件 30张PPT 2023-2024学年初中数学冀教版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 200.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 11:37:23 | ||
图片预览











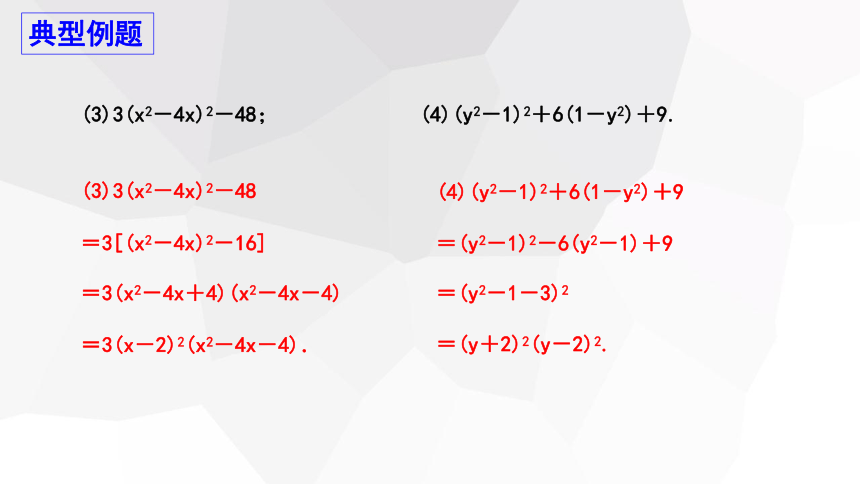
文档简介
(共30张PPT)
第十一章 因式分解
复习课
一、学习目标
1.理解因式分解的概念,并能根据因式分解与整式乘法的关系解题;
2.知道因式分解的方法、步骤,并能熟练应用因式分解的各种方法
进行因式分解;
3.能利用因式分解的方法解决实际问题.
二、知识结构
因式分解
概念:把一个多项式分解成几个整式乘积的形式
提公因式法
方法
公式法
a2-b2=(a+b)(a-b)
a2±2ab+b2=(a±b)2
公因式
整式乘法
三、知识回顾
知识点一 因式分解的概念
1.把一个多项式分解成几个整式乘积的形式,叫做多项式的因式分解.
3.多项式的因式分解是一个恒等变形.
2.因式分解的结果必须是几个整式乘积的形式;
注意:1.等号的左边必须是一个多项式;
2.多项式的因式分解与乘法运算是相反的变形过程.
典型例题
例1.下列各式从左边到右边的变形中,属于因式分解的是( )
A.(x+y)2=x2+2xy+y2 B.2x2-8=2(x+2)(x-2)
C.2x2-2x+1=2x(x-1)+1 D.(x+1)(x-1)=x2-1
B
解析:A项,是整式的乘法,故A不符合题意;B项,把一个多项式化成几个
整式的乘积的形式,故B符合题意;C项,没把一个多项式化成几个整式的
乘积的形式,故C不符合题意;D项,是整式的乘法,故D不符合题意.
典型例题
归纳总结:
(1)因式分解的最后结果是把一个多项式变形为几个整式乘积的形式;
(2)因式分解与整式乘法是两个相反的过程,可以利用整式乘法检验
因式分解是否正确.
【当堂检测】
1.下列变形,是因式分解的是( )
A. a(x+y)=ax+ay
B. x2+4xy+y2-1=x(x+4y)+(y+1)(y-1)
C. am2-a=a(m+1)(m-1)
D. m2-9n2+3=(m+3n)(m-3n)+3.
C
知识点二 因式分解的方法及步骤
三、知识回顾
1.提公因式法分解因式
(1)确定公因式:当多项式的各项系数都是整数时,公因式的系数应取各项
系数的最大公约数,字母应取各项相同的字母,且相同字母的指数取次数
最低的.
(2)把公因式写在括号外面,将多项式写成整式乘积的形式.
三、知识回顾
2.公式法分解因式
(1)因式分解中的平方差公式:a2-b2=(a+b)(a-b);
平方差式的特征:
①可化为两个整式;②两项符号相反;③每一项都是整式的平方.
(2)因式分解中的完全平方公式:a2±2ab+b2=(a±b)2;
完全平方式的特征:(1)可化成三项式;(2)有两项符号相同,能写成两个
整式的平方的形式;(3)另一项是这两整式乘积的±2倍.
典型例题
例2.把下列各式分解因式:
(1)x(y-x)+y(y-x)-(x-y)2; (2)a5-a;
(3)3(x2-4x)2-48; (4)(y2-1)2+6(1-y2)+9.
解析:(1)中(x-y)2=(y-x)2,可直接提取公因式y-x;
(2)(3)先提公因式,再用公式法分解;(4)直接用公式法进行因式分解.
典型例题
解:
(1)x(y-x)+y(y-x)-(x-y)2
=a(a2+1)(a+1)(a-1).
=a(a2+1)(a2-1)
(2)a5-a=a(a4-1)
=2x(y-x).
=(y-x)(x+y-y+x)
=(y-x)[x+y-(y-x)]
=x(y-x)+y(y-x)-(y-x)2
(1)x(y-x)+y(y-x)-(x-y)2; (2)a5-a;
典型例题
(3)3(x2-4x)2-48; (4)(y2-1)2+6(1-y2)+9.
(3)3(x2-4x)2-48
=(y+2)2(y-2)2.
=3(x-2)2(x2-4x-4).
=3(x2-4x+4)(x2-4x-4)
=3[(x2-4x)2-16]
(4)(y2-1)2+6(1-y2)+9
=(y2-1)2-6(y2-1)+9
=(y2-1-3)2
典型例题
归纳总结:
因式分解的步骤是:
一提(提公因式)、二用(用公式法分解)、三检查(检查分解是否彻底).
【当堂检测】
2.分解因式:
(1)a(x-y)-b(x-y)-c(y-x)= ;
(2)(m-n)2-(n-m)(m-2n)= ;
(3)3x3-27xy2= ;
(4)3x2y+12xy2+12y3= .
(x-y)(a-b+c)
(m-n)·(2m-3n)
3x(x+3y)(x-3y)
3y(x+2y)2
【当堂检测】
(1) 18xy2 - 27x2y - 3y3 (2) 4a2- 16(a - 2)2.
3.因式分解(写出步骤).
解:
=-3y(3x-y)2.
(2) 4a2 -16(a - 2)2
(1) 18xy2-27x2y-3y3
=-3y(9x2-6xy+y2)
=(6a-8)(8-2a).
=[2a+4(a-2)][2a-4(a-2)]
=-4(3a-4)(a-4).
【当堂检测】
4.计算:(1)5752×6-4252×6; (2)20192-2018×2020-9992.
解:
(1)原式=6×(5752-4252)
=(1+999)×(1-999)=-998000.
=6×1000×150=900000.
=6×(575+425)×(575-425)
(2)原式=20192-(2019-1)×(2019+1)-9992
=20192-(20192-1)-9992=1-9992
三、知识回顾
问题1: 利用因式分解求代数式的值
代数式求值问题的解题思路是什么?化简代数式的方法有哪些?
典型例题
例3.若a-b=-7,ab=-2,求下列各式的值:
(1)a2b3-a3b2; (2)a3b-2a2b2+ab3.
解:
(1)因为a-b=-7,ab=-2,
=ab(a-b)2=(-2)×(-7)2=-98.
(2)a3b-2a2b2+ab3=ab(a2-2ab+b2)
所以a2b3-a3b2=a2b2(b-a)=(-2)2×7=28.
典型例题
归纳总结:在代数式求值问题中,解题的基本思路是先化简代数式,
把代数式化简至最简后再代入求值.但在不同问题中,化简的方法也不同,
如:利用整式的加减、整式的乘法、分解因式等,因此,应根据具体的题目
特点,灵活选用化简代数式的方法.
【当堂检测】
5.若m-n=0,求(m2+n2)2-4m2n2下的值.
解:
(m2+n2)2-4m2n2=(m2+n2)2-(2mn)2
=(m2+n2+2mn)(m2+n2-2mn)
=(m+n)2(m-n)2
当m-n=0,(m2+n2)2-4m2n2=0.
三、知识回顾
问题2: 与因式分解有关的数学思想
本章中整体思想主要体现在哪些方面?
典型例题
例4.已知a+b=3,ab=5,则代数式a3b+2a2b2+ab3的值为________.
45
解:a3b+2a2b2+ab3=ab(a2+2ab+b2)=ab(a+b)2.
点拨:先提取公因式,再将代数式化成完全平方式的形式,最后整体代入.
把a+b=3,ab=5代入原式,得5×32=45.
整体思想
典型例题
归纳总结:整体思想体现在求代数式的值中,需要把代数式变形成含有
已知代数式的形式;
【当堂检测】
(a+b)(a-b-1)
(x-1)(x2+1)
6.写出下列多项因式分解的结果.
(1)(a+b)(a-b)-a-b= ,
(2)x3-x2+x-1= .
【当堂检测】
7.已知a+b=5,ab=10,求a3b+2a2b2+ab3的值.
解:a3b+2a2b2+ab3=ab(a2+2ab+b2)
=ab(a+b)2
∵a+b=5,ab=10,
∴a3b+2a2b2+ab3=10×52=250.
典型例题
数形结合思想
例5.小戴同学动手剪了若干张如图所示的正方形与长方形纸片.
①拼成如图(b)所示的正方形,根据四张小纸片的面积之和等于大纸片(正方形)的面积,有a2+2ab+b2=(a+b)2,验证了完全平方公式(分解因式);
典型例题
②拼成如图(c)所示的长方形,可得a2+3ab+2b2=
(a+2b)(a+b),多项式a2+3ab+2b2分解因式的结果
表示长方形长、宽的两个整式a+2b与a+b的积.
问题:
(1)自己动手试一试,利用拼图分解因式a2+5ab+6b2= .
(2)猜想面积为2a2+5ab+2b2的长方形的长、宽可能分别为:
.
(a+2b)(a+3b)
a+2b,2a+b或2a+b,a+2b
典型例题
归纳总结:本章中数形结合思想主要体现在用长方形纸片的图形面积来解释
因式分解.利用几何图形的面积可以把整式乘法与因式分解有机地联系起来.
拓展:由整式的乘法得(x+p)(x+q)=x2+(p+q)x+pq;
那么反过来x2+(p+q)x+pq=(x+p)(x+q)也成立,在拼图过程中也验证了该式.
那么除了利用拼图将a2+5ab+6b2分解因式,也可以用如下方法:
a2+5ab+6b2=a2+(2b+3b)a+2b·3b=(a+2b)(a+3b).
【当堂检测】
(1)x2-5x+6; (2)x2﹣6x-7.
(1)原式=x2+[(-2)+(-3)]x+(-2)×(-3)=(x-2)(x-3);
(2)原式=x2+[(-7)+1]+(-7)×1=(x-7)(x+1).
7.因式分解.
四、课堂总结
因式分解
概念
定义:把一个多项式化成几个整式的积的形式.
与整式乘法的关系:互逆关系
因式分解的方法
提公因式法:1.确定公因式 2.提取公因式
公式法
平方差公式:a2-b2=(a+b)(a-b)
完全平方公式:a2±2ab+b2=(a±b)2
第十一章 因式分解
复习课
一、学习目标
1.理解因式分解的概念,并能根据因式分解与整式乘法的关系解题;
2.知道因式分解的方法、步骤,并能熟练应用因式分解的各种方法
进行因式分解;
3.能利用因式分解的方法解决实际问题.
二、知识结构
因式分解
概念:把一个多项式分解成几个整式乘积的形式
提公因式法
方法
公式法
a2-b2=(a+b)(a-b)
a2±2ab+b2=(a±b)2
公因式
整式乘法
三、知识回顾
知识点一 因式分解的概念
1.把一个多项式分解成几个整式乘积的形式,叫做多项式的因式分解.
3.多项式的因式分解是一个恒等变形.
2.因式分解的结果必须是几个整式乘积的形式;
注意:1.等号的左边必须是一个多项式;
2.多项式的因式分解与乘法运算是相反的变形过程.
典型例题
例1.下列各式从左边到右边的变形中,属于因式分解的是( )
A.(x+y)2=x2+2xy+y2 B.2x2-8=2(x+2)(x-2)
C.2x2-2x+1=2x(x-1)+1 D.(x+1)(x-1)=x2-1
B
解析:A项,是整式的乘法,故A不符合题意;B项,把一个多项式化成几个
整式的乘积的形式,故B符合题意;C项,没把一个多项式化成几个整式的
乘积的形式,故C不符合题意;D项,是整式的乘法,故D不符合题意.
典型例题
归纳总结:
(1)因式分解的最后结果是把一个多项式变形为几个整式乘积的形式;
(2)因式分解与整式乘法是两个相反的过程,可以利用整式乘法检验
因式分解是否正确.
【当堂检测】
1.下列变形,是因式分解的是( )
A. a(x+y)=ax+ay
B. x2+4xy+y2-1=x(x+4y)+(y+1)(y-1)
C. am2-a=a(m+1)(m-1)
D. m2-9n2+3=(m+3n)(m-3n)+3.
C
知识点二 因式分解的方法及步骤
三、知识回顾
1.提公因式法分解因式
(1)确定公因式:当多项式的各项系数都是整数时,公因式的系数应取各项
系数的最大公约数,字母应取各项相同的字母,且相同字母的指数取次数
最低的.
(2)把公因式写在括号外面,将多项式写成整式乘积的形式.
三、知识回顾
2.公式法分解因式
(1)因式分解中的平方差公式:a2-b2=(a+b)(a-b);
平方差式的特征:
①可化为两个整式;②两项符号相反;③每一项都是整式的平方.
(2)因式分解中的完全平方公式:a2±2ab+b2=(a±b)2;
完全平方式的特征:(1)可化成三项式;(2)有两项符号相同,能写成两个
整式的平方的形式;(3)另一项是这两整式乘积的±2倍.
典型例题
例2.把下列各式分解因式:
(1)x(y-x)+y(y-x)-(x-y)2; (2)a5-a;
(3)3(x2-4x)2-48; (4)(y2-1)2+6(1-y2)+9.
解析:(1)中(x-y)2=(y-x)2,可直接提取公因式y-x;
(2)(3)先提公因式,再用公式法分解;(4)直接用公式法进行因式分解.
典型例题
解:
(1)x(y-x)+y(y-x)-(x-y)2
=a(a2+1)(a+1)(a-1).
=a(a2+1)(a2-1)
(2)a5-a=a(a4-1)
=2x(y-x).
=(y-x)(x+y-y+x)
=(y-x)[x+y-(y-x)]
=x(y-x)+y(y-x)-(y-x)2
(1)x(y-x)+y(y-x)-(x-y)2; (2)a5-a;
典型例题
(3)3(x2-4x)2-48; (4)(y2-1)2+6(1-y2)+9.
(3)3(x2-4x)2-48
=(y+2)2(y-2)2.
=3(x-2)2(x2-4x-4).
=3(x2-4x+4)(x2-4x-4)
=3[(x2-4x)2-16]
(4)(y2-1)2+6(1-y2)+9
=(y2-1)2-6(y2-1)+9
=(y2-1-3)2
典型例题
归纳总结:
因式分解的步骤是:
一提(提公因式)、二用(用公式法分解)、三检查(检查分解是否彻底).
【当堂检测】
2.分解因式:
(1)a(x-y)-b(x-y)-c(y-x)= ;
(2)(m-n)2-(n-m)(m-2n)= ;
(3)3x3-27xy2= ;
(4)3x2y+12xy2+12y3= .
(x-y)(a-b+c)
(m-n)·(2m-3n)
3x(x+3y)(x-3y)
3y(x+2y)2
【当堂检测】
(1) 18xy2 - 27x2y - 3y3 (2) 4a2- 16(a - 2)2.
3.因式分解(写出步骤).
解:
=-3y(3x-y)2.
(2) 4a2 -16(a - 2)2
(1) 18xy2-27x2y-3y3
=-3y(9x2-6xy+y2)
=(6a-8)(8-2a).
=[2a+4(a-2)][2a-4(a-2)]
=-4(3a-4)(a-4).
【当堂检测】
4.计算:(1)5752×6-4252×6; (2)20192-2018×2020-9992.
解:
(1)原式=6×(5752-4252)
=(1+999)×(1-999)=-998000.
=6×1000×150=900000.
=6×(575+425)×(575-425)
(2)原式=20192-(2019-1)×(2019+1)-9992
=20192-(20192-1)-9992=1-9992
三、知识回顾
问题1: 利用因式分解求代数式的值
代数式求值问题的解题思路是什么?化简代数式的方法有哪些?
典型例题
例3.若a-b=-7,ab=-2,求下列各式的值:
(1)a2b3-a3b2; (2)a3b-2a2b2+ab3.
解:
(1)因为a-b=-7,ab=-2,
=ab(a-b)2=(-2)×(-7)2=-98.
(2)a3b-2a2b2+ab3=ab(a2-2ab+b2)
所以a2b3-a3b2=a2b2(b-a)=(-2)2×7=28.
典型例题
归纳总结:在代数式求值问题中,解题的基本思路是先化简代数式,
把代数式化简至最简后再代入求值.但在不同问题中,化简的方法也不同,
如:利用整式的加减、整式的乘法、分解因式等,因此,应根据具体的题目
特点,灵活选用化简代数式的方法.
【当堂检测】
5.若m-n=0,求(m2+n2)2-4m2n2下的值.
解:
(m2+n2)2-4m2n2=(m2+n2)2-(2mn)2
=(m2+n2+2mn)(m2+n2-2mn)
=(m+n)2(m-n)2
当m-n=0,(m2+n2)2-4m2n2=0.
三、知识回顾
问题2: 与因式分解有关的数学思想
本章中整体思想主要体现在哪些方面?
典型例题
例4.已知a+b=3,ab=5,则代数式a3b+2a2b2+ab3的值为________.
45
解:a3b+2a2b2+ab3=ab(a2+2ab+b2)=ab(a+b)2.
点拨:先提取公因式,再将代数式化成完全平方式的形式,最后整体代入.
把a+b=3,ab=5代入原式,得5×32=45.
整体思想
典型例题
归纳总结:整体思想体现在求代数式的值中,需要把代数式变形成含有
已知代数式的形式;
【当堂检测】
(a+b)(a-b-1)
(x-1)(x2+1)
6.写出下列多项因式分解的结果.
(1)(a+b)(a-b)-a-b= ,
(2)x3-x2+x-1= .
【当堂检测】
7.已知a+b=5,ab=10,求a3b+2a2b2+ab3的值.
解:a3b+2a2b2+ab3=ab(a2+2ab+b2)
=ab(a+b)2
∵a+b=5,ab=10,
∴a3b+2a2b2+ab3=10×52=250.
典型例题
数形结合思想
例5.小戴同学动手剪了若干张如图所示的正方形与长方形纸片.
①拼成如图(b)所示的正方形,根据四张小纸片的面积之和等于大纸片(正方形)的面积,有a2+2ab+b2=(a+b)2,验证了完全平方公式(分解因式);
典型例题
②拼成如图(c)所示的长方形,可得a2+3ab+2b2=
(a+2b)(a+b),多项式a2+3ab+2b2分解因式的结果
表示长方形长、宽的两个整式a+2b与a+b的积.
问题:
(1)自己动手试一试,利用拼图分解因式a2+5ab+6b2= .
(2)猜想面积为2a2+5ab+2b2的长方形的长、宽可能分别为:
.
(a+2b)(a+3b)
a+2b,2a+b或2a+b,a+2b
典型例题
归纳总结:本章中数形结合思想主要体现在用长方形纸片的图形面积来解释
因式分解.利用几何图形的面积可以把整式乘法与因式分解有机地联系起来.
拓展:由整式的乘法得(x+p)(x+q)=x2+(p+q)x+pq;
那么反过来x2+(p+q)x+pq=(x+p)(x+q)也成立,在拼图过程中也验证了该式.
那么除了利用拼图将a2+5ab+6b2分解因式,也可以用如下方法:
a2+5ab+6b2=a2+(2b+3b)a+2b·3b=(a+2b)(a+3b).
【当堂检测】
(1)x2-5x+6; (2)x2﹣6x-7.
(1)原式=x2+[(-2)+(-3)]x+(-2)×(-3)=(x-2)(x-3);
(2)原式=x2+[(-7)+1]+(-7)×1=(x-7)(x+1).
7.因式分解.
四、课堂总结
因式分解
概念
定义:把一个多项式化成几个整式的积的形式.
与整式乘法的关系:互逆关系
因式分解的方法
提公因式法:1.确定公因式 2.提取公因式
公式法
平方差公式:a2-b2=(a+b)(a-b)
完全平方公式:a2±2ab+b2=(a±b)2
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
