5.2.1 平行线 课件(共14张PPT) 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 5.2.1 平行线 课件(共14张PPT) 2023-2024学年初中数学人教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 11:09:04 | ||
图片预览





文档简介
(共14张PPT)
5.2 平行线及其判定
5.2.1 平行线
第五章 相交线与平行线
1.理解平行线的概念,探索并掌握平行公理及推论.
任务:理解平行线的概念,探索并掌握平行公理及推论
活动1:如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
问题1:顺时针转动a,直线a与直线b的交点位置将发生什么变化
a
b
c
问题2:在这个过程中, 有没有直线a与b不相交的位置
在同一平面内,不相交的两条直线叫做平行线.
新知生成
表示方法:平行用符号“∥”表示,
如直线a与直线b平行,记作:a∥b,读作“a平行于b”.
a
b
c
在同一平面内,两条直线有几种位置关系?动手画一画?
思考
归纳
在同一平面内,两直线的位置关系有平行与相交两种.
练一练
下列说法中正确的有: .
(1)在同一平面内不相交的两条线段必平行;
(2)在同一平面内不相交的两条直线必平行;
(3)在同一平面内不平行的两条线段必相交;
(4)在同一平面内不平行的两条直线必相交;
(5)在同一平面内,两条直线的位置关系有三种:平行、相交和垂直.
(2)(4)
平行线画法
1、放;2、靠;3、推;4、画.
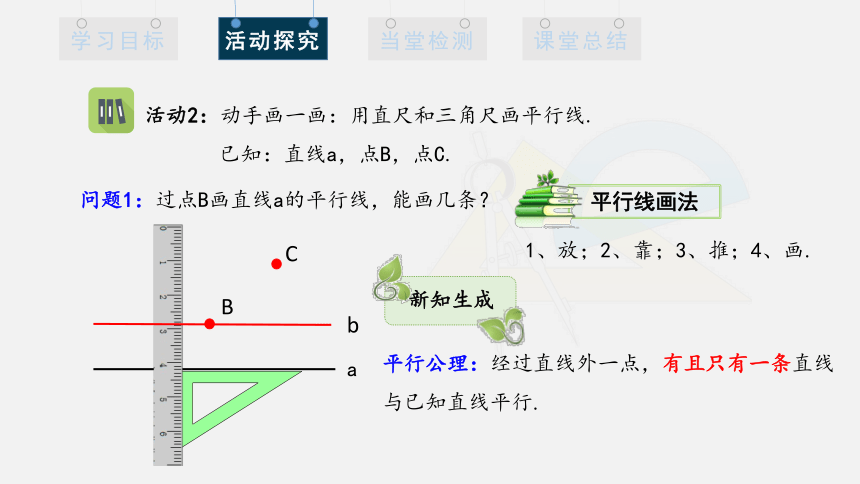
活动2:动手画一画:用直尺和三角尺画平行线.
已知:直线a,点B,点C.
问题1:过点B画直线a的平行线,能画几条?
B
C
a
b
平行公理:经过直线外一点,有且只有一条直线与已知直线平行.
新知生成
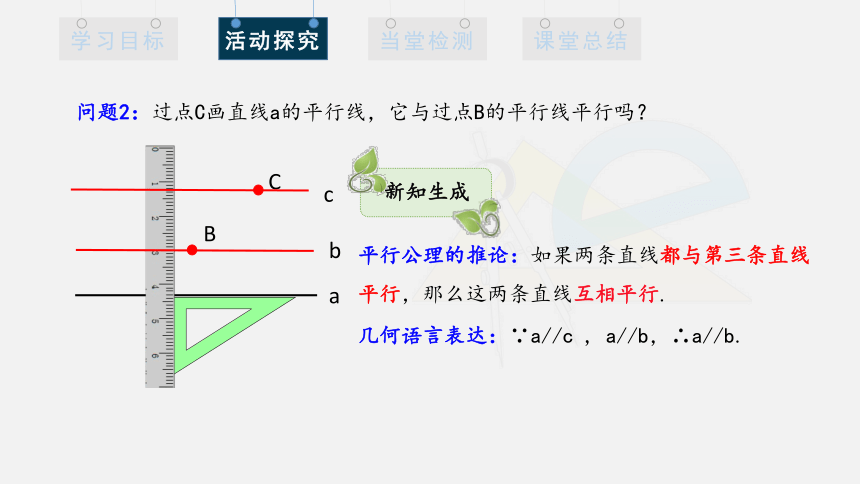
问题2:过点C画直线a的平行线,它与过点B的平行线平行吗?
B
C
b
a
c
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线互相平行.
新知生成
几何语言表达:∵a//c , a//b,∴a//b.
练一练
1.四条直线a,b,c,d互不重合,如果a∥b,b∥c,c∥d,那么直线a,d的位置关系为 .
a∥d
2.直线AB,CD是相交直线,点P是直线AB,CD外的一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E.
A
B
C
D
P
E
1.下列说法不正确的是( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
A
2.判断正误:
(1)在同一平面内,两条不平行的直线是相交线( )
(2)与同一条直线平行的两条直线必平行( )
(3)与同一条直线相交的两条直线必相交( )
(4)过直线外一点有且只有一条直线与已知直线平行( )
×
√
√
√
3.在同一平面内的两条直线a,b,根据下列的条件,写出a,b的位置关系.
(1)如果它们没有公共点,则________.
(2)如果它们都平行于第三条直线,则________.
(3)如果它们有且只有一个公共点,则__________.
(4)过平面内的同一点画它们的平行线,能画出两条,则__________.
a∥b
a和b相交
a和b相交
a∥b
4.如图,AD∥BC,在AB上取一点M,过M画MN∥BC交CD于N,并说明MN与AD的位置关系,为什么?
解:MN∥AD.
理由:因为AD∥BC,MN∥BC,所以MN∥AD.
本课关键词:
1.平行线;
3.平行公理的推论.
2.平行公理;
用自己的话,说一说今天我们学习了哪些知识?
5.2 平行线及其判定
5.2.1 平行线
第五章 相交线与平行线
1.理解平行线的概念,探索并掌握平行公理及推论.
任务:理解平行线的概念,探索并掌握平行公理及推论
活动1:如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
问题1:顺时针转动a,直线a与直线b的交点位置将发生什么变化
a
b
c
问题2:在这个过程中, 有没有直线a与b不相交的位置
在同一平面内,不相交的两条直线叫做平行线.
新知生成
表示方法:平行用符号“∥”表示,
如直线a与直线b平行,记作:a∥b,读作“a平行于b”.
a
b
c
在同一平面内,两条直线有几种位置关系?动手画一画?
思考
归纳
在同一平面内,两直线的位置关系有平行与相交两种.
练一练
下列说法中正确的有: .
(1)在同一平面内不相交的两条线段必平行;
(2)在同一平面内不相交的两条直线必平行;
(3)在同一平面内不平行的两条线段必相交;
(4)在同一平面内不平行的两条直线必相交;
(5)在同一平面内,两条直线的位置关系有三种:平行、相交和垂直.
(2)(4)
平行线画法
1、放;2、靠;3、推;4、画.
活动2:动手画一画:用直尺和三角尺画平行线.
已知:直线a,点B,点C.
问题1:过点B画直线a的平行线,能画几条?
B
C
a
b
平行公理:经过直线外一点,有且只有一条直线与已知直线平行.
新知生成
问题2:过点C画直线a的平行线,它与过点B的平行线平行吗?
B
C
b
a
c
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线互相平行.
新知生成
几何语言表达:∵a//c , a//b,∴a//b.
练一练
1.四条直线a,b,c,d互不重合,如果a∥b,b∥c,c∥d,那么直线a,d的位置关系为 .
a∥d
2.直线AB,CD是相交直线,点P是直线AB,CD外的一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E.
A
B
C
D
P
E
1.下列说法不正确的是( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
A
2.判断正误:
(1)在同一平面内,两条不平行的直线是相交线( )
(2)与同一条直线平行的两条直线必平行( )
(3)与同一条直线相交的两条直线必相交( )
(4)过直线外一点有且只有一条直线与已知直线平行( )
×
√
√
√
3.在同一平面内的两条直线a,b,根据下列的条件,写出a,b的位置关系.
(1)如果它们没有公共点,则________.
(2)如果它们都平行于第三条直线,则________.
(3)如果它们有且只有一个公共点,则__________.
(4)过平面内的同一点画它们的平行线,能画出两条,则__________.
a∥b
a和b相交
a和b相交
a∥b
4.如图,AD∥BC,在AB上取一点M,过M画MN∥BC交CD于N,并说明MN与AD的位置关系,为什么?
解:MN∥AD.
理由:因为AD∥BC,MN∥BC,所以MN∥AD.
本课关键词:
1.平行线;
3.平行公理的推论.
2.平行公理;
用自己的话,说一说今天我们学习了哪些知识?
