2023-2024学年初中数学人教版八年级下册17.1 勾股定理 第2课时课件(共29张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册17.1 勾股定理 第2课时课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 11:46:30 | ||
图片预览





文档简介
(共29张PPT)
第十七章 勾股定理
17.1 勾股定理
第2课时
1.会通过建立直角三角形模型,运用直角三角形的性质(勾股定理)
求线段长度、解决一些简单的实际问题.
活动探究
学习目标
当堂检测
课堂总结
(1)如图,电工师傅准备从电线杆离地面8m处的A点向地面拉一条钢索来稳固电线杆,已知这条钢索在地面的固定点B距离电线杆底部C点6m,问:地面,电线杆,钢索构成了怎样的图形?电工师傅至少应准备多长的钢索呢?
A
B
C
任务:利用勾股定理求线段长、解决简单的实际问题
活动1:请尝试解答下列问题,说说你的解题思路或方法.
解:地面,电线杆,钢索构成了一个直角三角形,
由勾股定理可得,
AB2=AC2+BC2,
则 (m)
因此,电工师傅至少应准备10 m长的钢索.
活动探究
学习目标
当堂检测
课堂总结
活动探究
学习目标
当堂检测
课堂总结
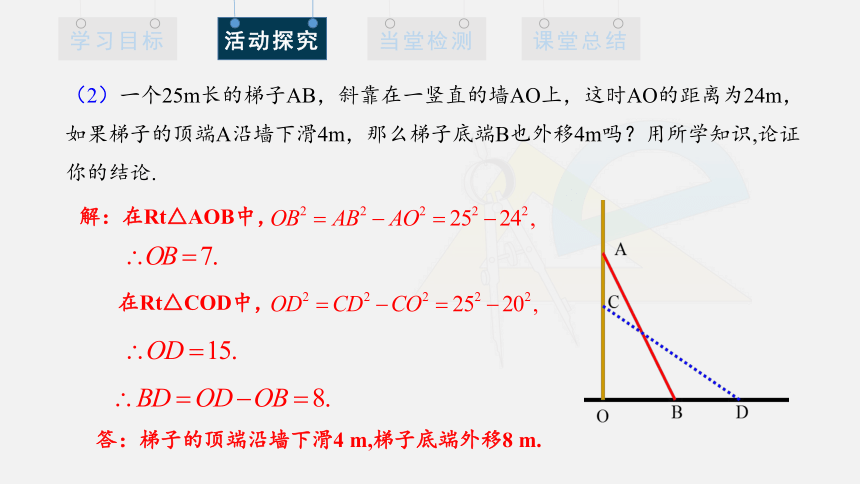
(2)一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为24m,
如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4m吗?用所学知识,论证
你的结论.
答:梯子的顶端沿墙下滑4 m,梯子底端外移8 m.
解:在Rt△AOB中,
在Rt△COD中,
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知量、未知量间的关系;
(2)构造直角三角形;
(3)利用勾股定理解答,确定实际问题的答案.
活动小结
活动探究
学习目标
当堂检测
课堂总结
活动探究
学习目标
当堂检测
课堂总结
练一练
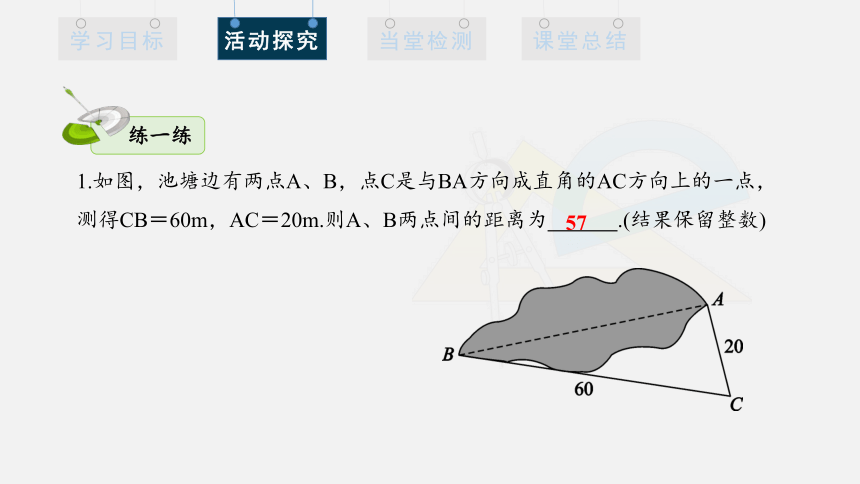
1.如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,
测得CB=60m,AC=20m.则A、B两点间的距离为 .(结果保留整数)
57
活动探究
学习目标
当堂检测
课堂总结
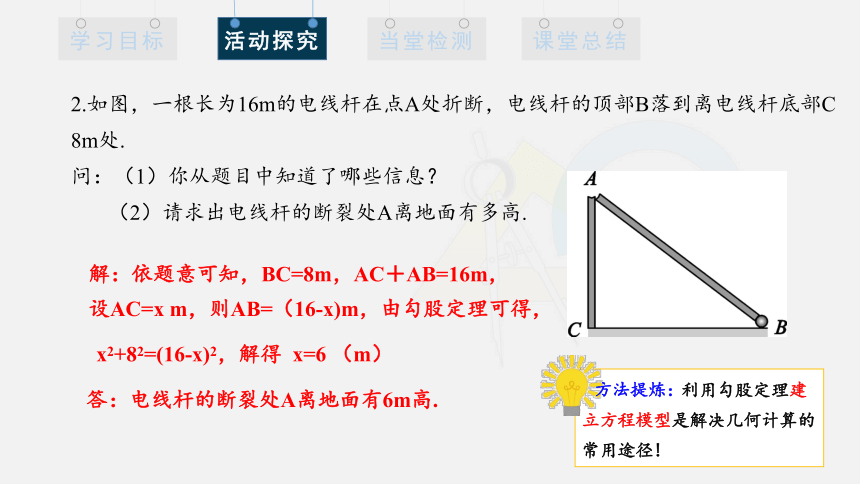
2.如图,一根长为16m的电线杆在点A处折断,电线杆的顶部B落到离电线杆底部C 8m处.
问:(1)你从题目中知道了哪些信息?
(2)请求出电线杆的断裂处A离地面有多高.
解:依题意可知,BC=8m,AC+AB=16m,
设AC=x m,则AB=(16-x)m,由勾股定理可得,
x2+82=(16-x)2,解得 x=6 (m)
答:电线杆的断裂处A离地面有6m高.
利用勾股定理建立方程模型是解决几何计算的常用途径!
方法提炼:
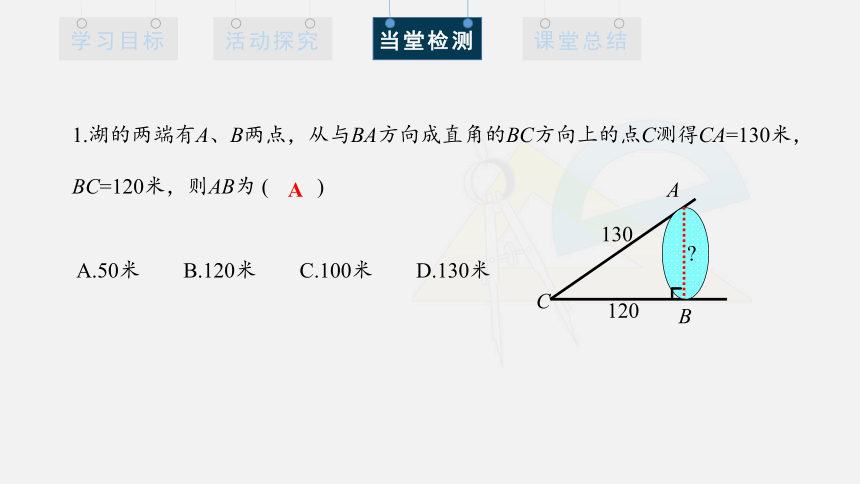
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,BC=120米,则AB为 ( )
A.50米 B.120米 C.100米 D.130米
A
B
C
130
120
A
2.如图,有两棵树,一棵高8米,另一棵2米,两棵树相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
解:如图,过点A作AC⊥BC于点C.
答:小鸟至少飞行10米.
由题意得AC=8米,BC=8-2=6(米),
=10(米)
3.如图,有一个高1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分是0.5米,问这根铁棒的长在什么范围内
当最短时:x=1.5,即伸入油桶中最短的长度是1.5+0.5=2(米).
解:设伸入油桶中的长度为x米,则应求最长时和最短时的值.
当最长时:x2=1.52 + 22,
即x2=6.25,
解得 x=2.5,
所以伸入油桶中最长的长度是2.5+0.5=3(米).
答:这根铁棒的长应在2~3米之间(包含2米、3米).
本节课主要解决了什么问题,你能说一说你学到了哪些知识或方法吗?
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
第十七章 勾股定理
17.1 勾股定理
第3课时
1.掌握利用勾股定理证明“HL”的方法
2.经历探索用勾股定理在数轴上表示无理数的过程,掌握在数轴上
(或网格中)表示无理数的方法.
3.能用勾股定理解决在直角坐标系或网格中求线段长度等问题.
活动探究
学习目标
当堂检测
课堂总结
活动探究
学习目标
当堂检测
课堂总结
任务一:掌握利用勾股定理证明“HL”的方法
活动:我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.请画出图形,写出已知、求证,并用勾股定理证明这一定理.
已知:如图,在Rt△ABC和Rt△A'B'C'中,
∠C=∠C'=90°,AB=A'B',AC=A'C',
求证:△ABC≌△A'B'C'.
活动探究
学习目标
当堂检测
课堂总结
A
B
C
A
B
C′
′
′
证明:在Rt△ABC和Rt△A'B'C'中,
∠C=∠C'=90°,根据勾股定理,得:
又 AB=A'B',AC=A'C',
∴BC=B'C'.
∴△ABC≌△A'B'C'(SSS).
活动探究
学习目标
当堂检测
课堂总结
任务二:探究并掌握在数轴上表示无理数的方法
活动:用所学知识,解答下列问题:
(1) 请求出下列直角三角形的斜边,并在数轴上表示出这些边长的点.(说说你的作法,保留作图痕迹)
(2)观察右下角的“海螺型”图案,与同伴交流,尝试
分析这个“海螺型”图案是如何形成的.
2
1
2
3
1
.
1
.
.
活动探究
学习目标
当堂检测
课堂总结
0
1
2
3
4
作图步骤:(以 为例):
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以确定C点.
活动探究
学习目标
当堂检测
课堂总结
类似地,利用勾股定理可以作出长为 …的线段(如图1),同样,
可以在数轴上作出表示 …的点(如图2).
-1 0 1 2 3
图1
图2
活动探究
学习目标
当堂检测
课堂总结
在数轴上表示无理数的方法:
1.利用勾股定理把要表示的无理数中根号下的整数,拆分成两个整数的平方和的
形式,即可得出哪两条线段长的平方和等于所画线段(斜边)长的平方.
2.以数轴原点为直角三角形一条直角边的顶点,在数轴的正半轴上找到表示其中
较大整数的点作为直角顶点,过这点作数轴的垂线,构造直角三角形,找出斜边;
3.以数轴原点为圆心,以斜边长为半径画弧,即可在数轴上找到表示该无理数的点.
活动小结
活动探究
学习目标
当堂检测
课堂总结
练一练
1.在数轴上表示 的点在表示两个连续整数 的点之间.
4和5
2.在数轴上作出表示 的点.(不写作法,保留作图痕迹)
如下图所示,
2
l
0
1
2
3
4
解:长为 的线段可以看成是直角边长为正整数4,2的直角三角形的斜边.
活动探究
学习目标
当堂检测
课堂总结
任务三:用勾股定理解决在直角坐标系或网格中求线段长度等问题
活动:解答下列问题,小组整理、归纳解答中遇到的问题或注意事项.
(1)如图1,数轴上点A所表示的数为a,则a=________.
(2)如图2,正方形网格中,每个小正方形的边长为1,
求网格上的三角形ABC的面积和周长.
图1
图2
活动探究
学习目标
当堂检测
课堂总结
∴点A所表示的数为 .
解:(1)∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
(1)如图1,数轴上点A所表示的数为a,则a=________.
活动探究
学习目标
当堂检测
课堂总结
所以,△ABC的周长为
由勾股定理得
(2)如图2,正方形网格中,每个小正方形的边长为1,求网格上的三角形ABC的
面积和周长.
(2)S△ABC =
图2
活动探究
学习目标
当堂检测
课堂总结
(1)求数轴上点所表示的数时要注意观察画弧的起点是否是原点,准确确定斜边长.
(2)在网格的求线段长时,通常是把线段放在与网格构成的直角三角形中,再利用勾股定理求其长度.
活动小结
活动探究
学习目标
当堂检测
课堂总结
如图,点A表示的实数是 .
练一练
1.如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
C
2.如图,正方形网格中的每个小正方形的边长都是1,每个顶点叫做格点.
在图中以格点为顶点画一个面积为8的正方形;
解:如图所示,
面积为8的正方形的边长为 .
3.如图,网格中小正方形的边长均为1.你在网格中画出一个△ABC,要求:顶点都在格点(即小正方形的顶点)上;三边长满足AB= ,BC= ,AC= ,并求出该三角形的面积.
则S△ABC =
解:如图,△ABC即为所求:
A
B
C
本节课我们用勾股定理解决了哪些问题呢,说一说你都学到了哪些知识?
利用勾股定理
作图或计算
把一个无理数表示成直角边是两个正整数的直角三角形的斜边,再在数轴上(或网格线中)表示出该无理数
解决在坐标系或网格中求线段长度等问题
利用勾股定理
证明“HL”定理
第十七章 勾股定理
17.1 勾股定理
第2课时
1.会通过建立直角三角形模型,运用直角三角形的性质(勾股定理)
求线段长度、解决一些简单的实际问题.
活动探究
学习目标
当堂检测
课堂总结
(1)如图,电工师傅准备从电线杆离地面8m处的A点向地面拉一条钢索来稳固电线杆,已知这条钢索在地面的固定点B距离电线杆底部C点6m,问:地面,电线杆,钢索构成了怎样的图形?电工师傅至少应准备多长的钢索呢?
A
B
C
任务:利用勾股定理求线段长、解决简单的实际问题
活动1:请尝试解答下列问题,说说你的解题思路或方法.
解:地面,电线杆,钢索构成了一个直角三角形,
由勾股定理可得,
AB2=AC2+BC2,
则 (m)
因此,电工师傅至少应准备10 m长的钢索.
活动探究
学习目标
当堂检测
课堂总结
活动探究
学习目标
当堂检测
课堂总结
(2)一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为24m,
如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4m吗?用所学知识,论证
你的结论.
答:梯子的顶端沿墙下滑4 m,梯子底端外移8 m.
解:在Rt△AOB中,
在Rt△COD中,
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知量、未知量间的关系;
(2)构造直角三角形;
(3)利用勾股定理解答,确定实际问题的答案.
活动小结
活动探究
学习目标
当堂检测
课堂总结
活动探究
学习目标
当堂检测
课堂总结
练一练
1.如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,
测得CB=60m,AC=20m.则A、B两点间的距离为 .(结果保留整数)
57
活动探究
学习目标
当堂检测
课堂总结
2.如图,一根长为16m的电线杆在点A处折断,电线杆的顶部B落到离电线杆底部C 8m处.
问:(1)你从题目中知道了哪些信息?
(2)请求出电线杆的断裂处A离地面有多高.
解:依题意可知,BC=8m,AC+AB=16m,
设AC=x m,则AB=(16-x)m,由勾股定理可得,
x2+82=(16-x)2,解得 x=6 (m)
答:电线杆的断裂处A离地面有6m高.
利用勾股定理建立方程模型是解决几何计算的常用途径!
方法提炼:
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,BC=120米,则AB为 ( )
A.50米 B.120米 C.100米 D.130米
A
B
C
130
120
A
2.如图,有两棵树,一棵高8米,另一棵2米,两棵树相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
解:如图,过点A作AC⊥BC于点C.
答:小鸟至少飞行10米.
由题意得AC=8米,BC=8-2=6(米),
=10(米)
3.如图,有一个高1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分是0.5米,问这根铁棒的长在什么范围内
当最短时:x=1.5,即伸入油桶中最短的长度是1.5+0.5=2(米).
解:设伸入油桶中的长度为x米,则应求最长时和最短时的值.
当最长时:x2=1.52 + 22,
即x2=6.25,
解得 x=2.5,
所以伸入油桶中最长的长度是2.5+0.5=3(米).
答:这根铁棒的长应在2~3米之间(包含2米、3米).
本节课主要解决了什么问题,你能说一说你学到了哪些知识或方法吗?
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
解决
第十七章 勾股定理
17.1 勾股定理
第3课时
1.掌握利用勾股定理证明“HL”的方法
2.经历探索用勾股定理在数轴上表示无理数的过程,掌握在数轴上
(或网格中)表示无理数的方法.
3.能用勾股定理解决在直角坐标系或网格中求线段长度等问题.
活动探究
学习目标
当堂检测
课堂总结
活动探究
学习目标
当堂检测
课堂总结
任务一:掌握利用勾股定理证明“HL”的方法
活动:我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.请画出图形,写出已知、求证,并用勾股定理证明这一定理.
已知:如图,在Rt△ABC和Rt△A'B'C'中,
∠C=∠C'=90°,AB=A'B',AC=A'C',
求证:△ABC≌△A'B'C'.
活动探究
学习目标
当堂检测
课堂总结
A
B
C
A
B
C′
′
′
证明:在Rt△ABC和Rt△A'B'C'中,
∠C=∠C'=90°,根据勾股定理,得:
又 AB=A'B',AC=A'C',
∴BC=B'C'.
∴△ABC≌△A'B'C'(SSS).
活动探究
学习目标
当堂检测
课堂总结
任务二:探究并掌握在数轴上表示无理数的方法
活动:用所学知识,解答下列问题:
(1) 请求出下列直角三角形的斜边,并在数轴上表示出这些边长的点.(说说你的作法,保留作图痕迹)
(2)观察右下角的“海螺型”图案,与同伴交流,尝试
分析这个“海螺型”图案是如何形成的.
2
1
2
3
1
.
1
.
.
活动探究
学习目标
当堂检测
课堂总结
0
1
2
3
4
作图步骤:(以 为例):
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以确定C点.
活动探究
学习目标
当堂检测
课堂总结
类似地,利用勾股定理可以作出长为 …的线段(如图1),同样,
可以在数轴上作出表示 …的点(如图2).
-1 0 1 2 3
图1
图2
活动探究
学习目标
当堂检测
课堂总结
在数轴上表示无理数的方法:
1.利用勾股定理把要表示的无理数中根号下的整数,拆分成两个整数的平方和的
形式,即可得出哪两条线段长的平方和等于所画线段(斜边)长的平方.
2.以数轴原点为直角三角形一条直角边的顶点,在数轴的正半轴上找到表示其中
较大整数的点作为直角顶点,过这点作数轴的垂线,构造直角三角形,找出斜边;
3.以数轴原点为圆心,以斜边长为半径画弧,即可在数轴上找到表示该无理数的点.
活动小结
活动探究
学习目标
当堂检测
课堂总结
练一练
1.在数轴上表示 的点在表示两个连续整数 的点之间.
4和5
2.在数轴上作出表示 的点.(不写作法,保留作图痕迹)
如下图所示,
2
l
0
1
2
3
4
解:长为 的线段可以看成是直角边长为正整数4,2的直角三角形的斜边.
活动探究
学习目标
当堂检测
课堂总结
任务三:用勾股定理解决在直角坐标系或网格中求线段长度等问题
活动:解答下列问题,小组整理、归纳解答中遇到的问题或注意事项.
(1)如图1,数轴上点A所表示的数为a,则a=________.
(2)如图2,正方形网格中,每个小正方形的边长为1,
求网格上的三角形ABC的面积和周长.
图1
图2
活动探究
学习目标
当堂检测
课堂总结
∴点A所表示的数为 .
解:(1)∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
(1)如图1,数轴上点A所表示的数为a,则a=________.
活动探究
学习目标
当堂检测
课堂总结
所以,△ABC的周长为
由勾股定理得
(2)如图2,正方形网格中,每个小正方形的边长为1,求网格上的三角形ABC的
面积和周长.
(2)S△ABC =
图2
活动探究
学习目标
当堂检测
课堂总结
(1)求数轴上点所表示的数时要注意观察画弧的起点是否是原点,准确确定斜边长.
(2)在网格的求线段长时,通常是把线段放在与网格构成的直角三角形中,再利用勾股定理求其长度.
活动小结
活动探究
学习目标
当堂检测
课堂总结
如图,点A表示的实数是 .
练一练
1.如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴于点M,则点M表示的数为( )
C
2.如图,正方形网格中的每个小正方形的边长都是1,每个顶点叫做格点.
在图中以格点为顶点画一个面积为8的正方形;
解:如图所示,
面积为8的正方形的边长为 .
3.如图,网格中小正方形的边长均为1.你在网格中画出一个△ABC,要求:顶点都在格点(即小正方形的顶点)上;三边长满足AB= ,BC= ,AC= ,并求出该三角形的面积.
则S△ABC =
解:如图,△ABC即为所求:
A
B
C
本节课我们用勾股定理解决了哪些问题呢,说一说你都学到了哪些知识?
利用勾股定理
作图或计算
把一个无理数表示成直角边是两个正整数的直角三角形的斜边,再在数轴上(或网格线中)表示出该无理数
解决在坐标系或网格中求线段长度等问题
利用勾股定理
证明“HL”定理
