2023-2024学年初中数学人教版八年级下册17.2 勾股定理的逆定理课件(共19张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册17.2 勾股定理的逆定理课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 11:49:18 | ||
图片预览






文档简介
(共19张PPT)
第十七章 勾股定理
17.2 勾股定理的逆定理
1.理解原命题、逆命题、逆定理的概念及关系.
2.会用勾股定理的逆定理判断直角三角形,会应用勾股定理及其
逆定理解决问题
活动探究
学习目标
当堂检测
课堂总结
任务一:理解原命题、逆命题、逆定理的概念及关系
活动探究
学习目标
当堂检测
课堂总结
活动1:下面有四组数分别是一个三角形的三边长a, b, c:
①4、7、9 ; ②5、12、13; ③7、24、25; 8、15、17.
(1)分别以每组数为三边长作出三角形,用量角器量一量,看看它们是否
都是直角三角形.
(2)观察确定为直角三角形的每组数据,找出它们的三边在数量关系上
有什么相同点,据此写出你的猜想.
④
活动探究
学习目标
当堂检测
课堂总结
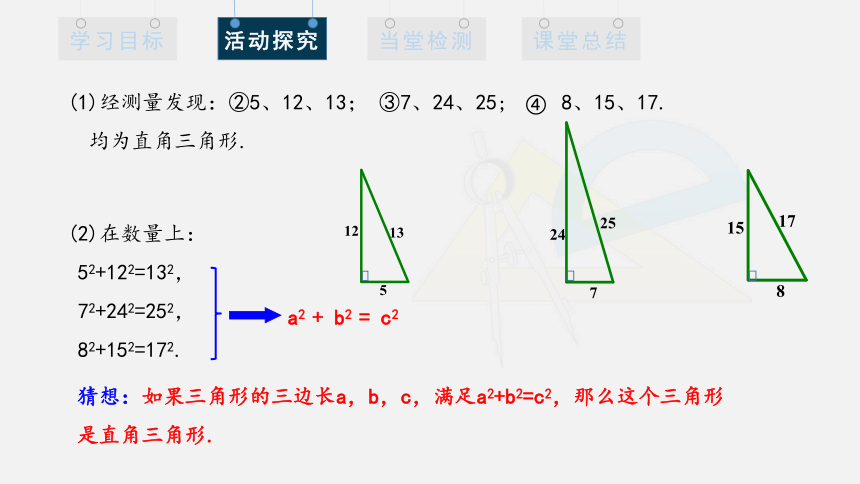
(1)经测量发现:②5、12、13; ③7、24、25; 8、15、17.
均为直角三角形.
④
(2)在数量上:
52+122=132,
72+242=252,
82+152=172.
a2 + b2 = c2
猜想:如果三角形的三边长a,b,c,满足a2+b2=c2,那么这个三角形
是直角三角形.
活动2:找出下面两个命题的题设与结论,说说两个命题之间有什么关系.
命题1:如果一个三角形是直角三角形,两直角边长为a,b,斜边长为c,那么
a2+b2=c2.(勾股定理)
命题2:如果三角形的三边长a,b,c,满足a2+b2=c2,那么这个三角形是
直角三角形.
活动探究
学习目标
当堂检测
课堂总结
题设和结论正好相反的两个命题叫做互逆命题.
如果把其中一个叫做原命题,那么另一个就是它的逆命题.
新知生成
活动探究
学习目标
当堂检测
课堂总结
1.请举出互逆命题的例子.
2.如果原命题正确,那么逆命题也正确吗 举例说明.
合作交流
3. 结合你判断直角三角形的经验,尝试说明命题2的真假性.
命题2:如果三角形的三边长a,b,c,满足a2+b2=c2,那么
这个三角形是直角三角形.
A
B
C
a
b
c
活动探究
学习目标
当堂检测
课堂总结
A
B
C
a
b
c
则A'B'2=B'C'2+A'C'2=a2+b2
∵a2 + b2 = c2,
∴A'B'2 = c2,A'B' = c
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS),
∴∠C=∠C'=90°,即△ABC是直角三角形.
证明:
作Rt△A'B'C',使∠C'=90°,A'C'=b,B'C'=a,
活动探究
学习目标
当堂检测
课堂总结
(1)如果三角形的三边长是a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形,是真命题,可以用来判定直角三角形,我们把它称为勾股定理的逆定理.
活动小结
(2)一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理“互为逆定理”.
活动探究
学习目标
当堂检测
课堂总结
1.关于定理“对顶角相等”的说法正确的为( )
A.它是逆定理 B.它有逆定理
C.它有逆命题 D.它没有逆命题
2.“角的内部到角的两边距离相等的点在角的平分线上”的逆定理是
.
练一练
角平分线上的点到角的两边的距离相等
C
活动探究
学习目标
当堂检测
课堂总结
任务二:运用勾股定理的逆定理、勾股定理解决问题
活动:一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为
直角,工人师傅量得这个零件各边的尺寸:DA=4,AB=3,BC=13,BD=5,CD=12.
(1) 这个零件符合要求吗 请验证你的结论.
(2) 求这个零件的面积.
(要求:请说说你的判断方法,谈谈你的收获)
D
A
B
C
活动探究
学习目标
当堂检测
课堂总结
D
A
B
C
4
3
5
13
12
所以△BCD 是直角三角形,∠DBC是直角.
解:(1)在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
在△BCD中,
因此,这个零件符合要求.
(1) 这个零件符合要求吗 请验证你的结论.
活动探究
学习目标
当堂检测
课堂总结
(2)这个零件的面积=△ABD的面积+△BDC的面积
=3×4÷2+5×12÷2
=6+30
=36
故这个零件的面积是36 .
D
A
B
C
4
3
5
13
12
(2) 求这个零件的面积.
活动探究
学习目标
当堂检测
课堂总结
利用勾股定理的逆定理判断三条线段能否构成直角三角形的方法如下:
1.排序:把三条线段按由小到大排列;
2.计算:看较小两条线段边的平方和是否等于最大线段的平方;
3.结论:判断能否构成直角三角形.(最长边所对应的角为直角)
活动小结
知识点拨:像3,4,5这样能够成为直角三角形的三条边长的三个正整数,称为勾股数.
活动探究
学习目标
当堂检测
课堂总结
下列由线段a,b,c组成的三角形是直角三角形有 ,其中a,b,c
是勾股数的有 .(填序号)
①a=6,b=8,c=10 ; ②a=1.5,b=2,c=2.5 .
练一练
①②
①
1.下列条件中,不能判断一个三角形是直角三角形的是 ( )
A.三条边的比为1∶2∶3
B.三条边满足关系a2=b2-c2
C.三条边的比为1∶1∶
D.三个角满足关系∠B+∠C=∠A
A
①a=13,b=14,c=15; ②a= ,b= ,c=1;③a=7,b=24,c=25;
(1)下列三组数中,是勾股数有 .(填序号)
(2)“如果两个实数相等,那么它们的绝对值相等.”的逆命题是:
,它是 命题.
③
2.填一填:
如果两个实数的绝对值相等,那么这两个实数相等
假
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组
也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时
A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:∵出发2小时,A组行进了12×2=24(km),
B组行进了9×2=18(km),
又∵A,B两组相距30km,
且有242+182=302,
∴A,B两组行进的方向成直角.
回顾本课所学知识,回答下列问题:
1.什么是原命题、逆命题、逆定理?
2.勾股定理的逆定理内容是什么?什么是勾股数?
3.勾股定理及其逆定理的应用有哪些?
应用
判定直角三角形
解决实际问题等
应用
第十七章 勾股定理
17.2 勾股定理的逆定理
1.理解原命题、逆命题、逆定理的概念及关系.
2.会用勾股定理的逆定理判断直角三角形,会应用勾股定理及其
逆定理解决问题
活动探究
学习目标
当堂检测
课堂总结
任务一:理解原命题、逆命题、逆定理的概念及关系
活动探究
学习目标
当堂检测
课堂总结
活动1:下面有四组数分别是一个三角形的三边长a, b, c:
①4、7、9 ; ②5、12、13; ③7、24、25; 8、15、17.
(1)分别以每组数为三边长作出三角形,用量角器量一量,看看它们是否
都是直角三角形.
(2)观察确定为直角三角形的每组数据,找出它们的三边在数量关系上
有什么相同点,据此写出你的猜想.
④
活动探究
学习目标
当堂检测
课堂总结
(1)经测量发现:②5、12、13; ③7、24、25; 8、15、17.
均为直角三角形.
④
(2)在数量上:
52+122=132,
72+242=252,
82+152=172.
a2 + b2 = c2
猜想:如果三角形的三边长a,b,c,满足a2+b2=c2,那么这个三角形
是直角三角形.
活动2:找出下面两个命题的题设与结论,说说两个命题之间有什么关系.
命题1:如果一个三角形是直角三角形,两直角边长为a,b,斜边长为c,那么
a2+b2=c2.(勾股定理)
命题2:如果三角形的三边长a,b,c,满足a2+b2=c2,那么这个三角形是
直角三角形.
活动探究
学习目标
当堂检测
课堂总结
题设和结论正好相反的两个命题叫做互逆命题.
如果把其中一个叫做原命题,那么另一个就是它的逆命题.
新知生成
活动探究
学习目标
当堂检测
课堂总结
1.请举出互逆命题的例子.
2.如果原命题正确,那么逆命题也正确吗 举例说明.
合作交流
3. 结合你判断直角三角形的经验,尝试说明命题2的真假性.
命题2:如果三角形的三边长a,b,c,满足a2+b2=c2,那么
这个三角形是直角三角形.
A
B
C
a
b
c
活动探究
学习目标
当堂检测
课堂总结
A
B
C
a
b
c
则A'B'2=B'C'2+A'C'2=a2+b2
∵a2 + b2 = c2,
∴A'B'2 = c2,A'B' = c
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS),
∴∠C=∠C'=90°,即△ABC是直角三角形.
证明:
作Rt△A'B'C',使∠C'=90°,A'C'=b,B'C'=a,
活动探究
学习目标
当堂检测
课堂总结
(1)如果三角形的三边长是a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形,是真命题,可以用来判定直角三角形,我们把它称为勾股定理的逆定理.
活动小结
(2)一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理“互为逆定理”.
活动探究
学习目标
当堂检测
课堂总结
1.关于定理“对顶角相等”的说法正确的为( )
A.它是逆定理 B.它有逆定理
C.它有逆命题 D.它没有逆命题
2.“角的内部到角的两边距离相等的点在角的平分线上”的逆定理是
.
练一练
角平分线上的点到角的两边的距离相等
C
活动探究
学习目标
当堂检测
课堂总结
任务二:运用勾股定理的逆定理、勾股定理解决问题
活动:一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为
直角,工人师傅量得这个零件各边的尺寸:DA=4,AB=3,BC=13,BD=5,CD=12.
(1) 这个零件符合要求吗 请验证你的结论.
(2) 求这个零件的面积.
(要求:请说说你的判断方法,谈谈你的收获)
D
A
B
C
活动探究
学习目标
当堂检测
课堂总结
D
A
B
C
4
3
5
13
12
所以△BCD 是直角三角形,∠DBC是直角.
解:(1)在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
在△BCD中,
因此,这个零件符合要求.
(1) 这个零件符合要求吗 请验证你的结论.
活动探究
学习目标
当堂检测
课堂总结
(2)这个零件的面积=△ABD的面积+△BDC的面积
=3×4÷2+5×12÷2
=6+30
=36
故这个零件的面积是36 .
D
A
B
C
4
3
5
13
12
(2) 求这个零件的面积.
活动探究
学习目标
当堂检测
课堂总结
利用勾股定理的逆定理判断三条线段能否构成直角三角形的方法如下:
1.排序:把三条线段按由小到大排列;
2.计算:看较小两条线段边的平方和是否等于最大线段的平方;
3.结论:判断能否构成直角三角形.(最长边所对应的角为直角)
活动小结
知识点拨:像3,4,5这样能够成为直角三角形的三条边长的三个正整数,称为勾股数.
活动探究
学习目标
当堂检测
课堂总结
下列由线段a,b,c组成的三角形是直角三角形有 ,其中a,b,c
是勾股数的有 .(填序号)
①a=6,b=8,c=10 ; ②a=1.5,b=2,c=2.5 .
练一练
①②
①
1.下列条件中,不能判断一个三角形是直角三角形的是 ( )
A.三条边的比为1∶2∶3
B.三条边满足关系a2=b2-c2
C.三条边的比为1∶1∶
D.三个角满足关系∠B+∠C=∠A
A
①a=13,b=14,c=15; ②a= ,b= ,c=1;③a=7,b=24,c=25;
(1)下列三组数中,是勾股数有 .(填序号)
(2)“如果两个实数相等,那么它们的绝对值相等.”的逆命题是:
,它是 命题.
③
2.填一填:
如果两个实数的绝对值相等,那么这两个实数相等
假
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组
也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时
A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:∵出发2小时,A组行进了12×2=24(km),
B组行进了9×2=18(km),
又∵A,B两组相距30km,
且有242+182=302,
∴A,B两组行进的方向成直角.
回顾本课所学知识,回答下列问题:
1.什么是原命题、逆命题、逆定理?
2.勾股定理的逆定理内容是什么?什么是勾股数?
3.勾股定理及其逆定理的应用有哪些?
应用
判定直角三角形
解决实际问题等
应用
