18.1.1 平行四边形的性质 (第2课时 ) 课件 13张PPT 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 18.1.1 平行四边形的性质 (第2课时 ) 课件 13张PPT 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
第十八章 平行四边形
18.1.1 平行四边形的性质
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解平行四边形对角线互相平分的性质.
2.综合运用平行四边形的性质进行有关的论证和计算.
活动探究
学习目标
当堂检测
课堂总结
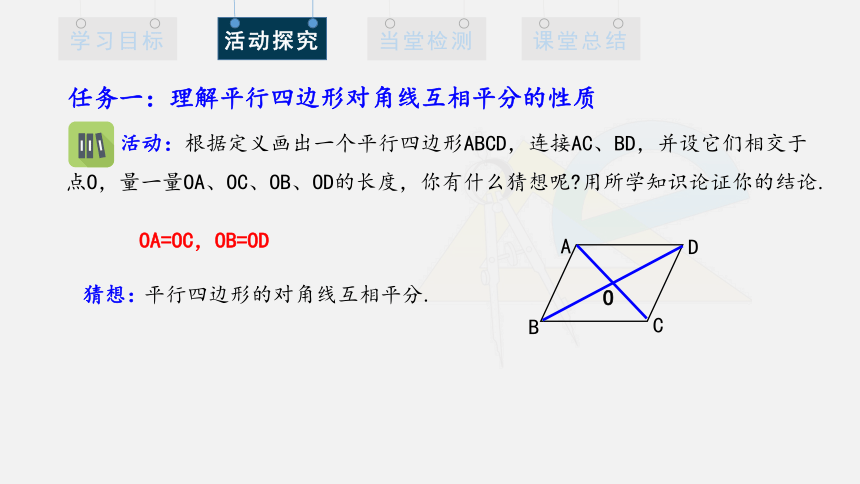
任务一:理解平行四边形对角线互相平分的性质
活动:根据定义画出一个平行四边形ABCD,连接AC、BD,并设它们相交于
点O,量一量OA、OC、OB、OD的长度,你有什么猜想呢 用所学知识论证你的结论.
A
B
D
C
O
OA=OC,OB=OD
猜想:
平行四边形的对角线互相平分.
活动探究
学习目标
当堂检测
课堂总结
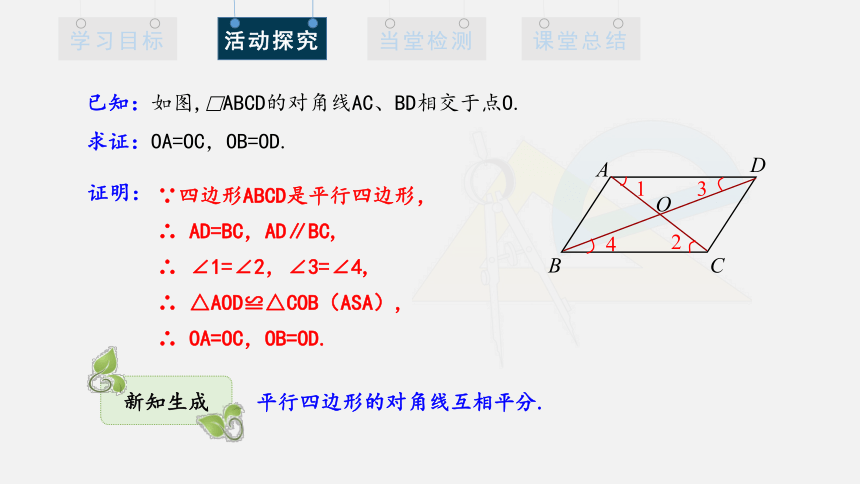
已知:如图,□ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
新知生成
平行四边形的对角线互相平分.
活动探究
学习目标
当堂检测
课堂总结
活动:请解决下列问题.(要求:写出解答过程,
小组归纳做题时遇到的问题、用到的性质或方法)
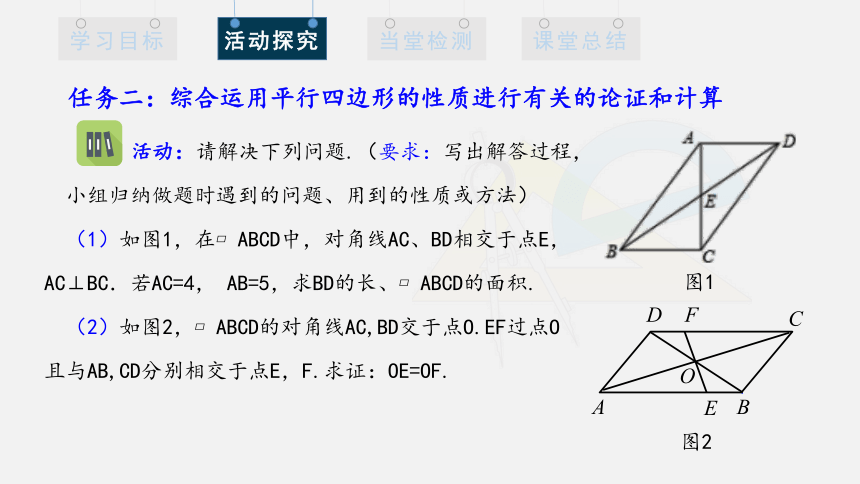
(1)如图1,在 ABCD中,对角线AC、BD相交于点E,
AC⊥BC.若AC=4, AB=5,求BD的长、 ABCD的面积.
(2)如图2, ABCD的对角线AC,BD交于点O.EF过点O
且与AB,CD分别相交于点E,F.求证:OE=OF.
任务二:综合运用平行四边形的性质进行有关的论证和计算
图1
图2
A
B
C
D
F
E
O
活动探究
学习目标
当堂检测
课堂总结
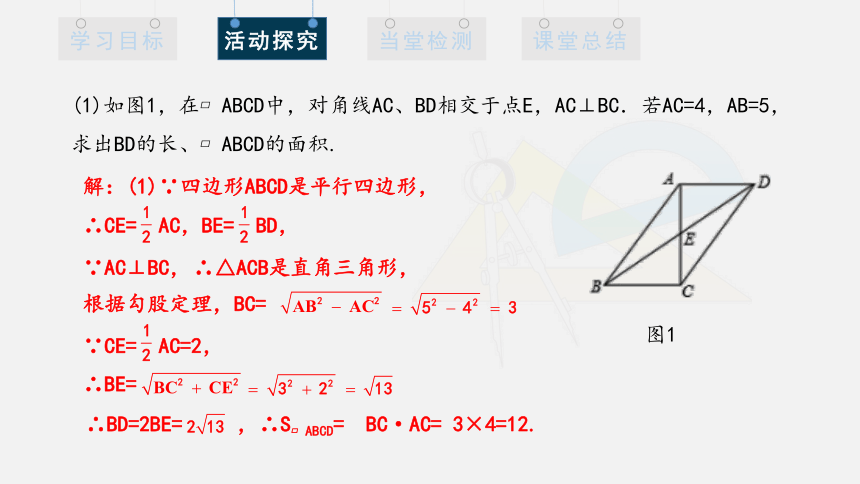
(1)如图1,在 ABCD中,对角线AC、BD相交于点E,AC⊥BC.若AC=4,AB=5,
求出BD的长、 ABCD的面积.
解:(1)∵四边形ABCD是平行四边形,
∵AC⊥BC,
∴△ACB是直角三角形,
∴CE= AC,BE= BD,
根据勾股定理,BC=
∵CE= AC=2,
∴BE=
∴BD=2BE= ,
∴S ABCD= BC·AC= 3×4=12.
图1
活动探究
学习目标
当堂检测
课堂总结
(2)如图2, ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.
求证:OE=OF.
图2
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD, OD=OB,
∴OE=OF.
活动探究
学习目标
当堂检测
课堂总结
活动小结
勾股定理与判定三角形全等是解决平行四边形中线段的计算或证明边、角
关系的的重要方法,要注意结合图形灵活运用平行四边形的性质,如对边平行
且相等、对角相等、两邻角互补、对角线互相平分,先找出边、角的关系,再
进行相关计算或证明.
活动探究
学习目标
当堂检测
课堂总结
练一练
如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则BD的长是 .
1.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OBC的周长为 ( )
A.26 B.34
C.40 D.52
B
2.如图,在 ABCD中,∠ODA=90°,AC=10,BD=6,则AD的长为 .
4
3.如图,在平行四边形ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
BE=DF,BE∥DF.
∴BE∥DF.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
∴OE=OF.
在△EOB和△FOD中
∴△EOB≌△FOD,
∴BE=DF,∠FDB=∠EBD,
∴BE=DF,BE∥DF.
4.一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了
一块平行四边形的土地,由于年迈体弱,他决定按照如下方法将这块土地分给
他的四个孩子,他的分法是否公平,请通过计算说明.
老大
老二
老三
老四
B
C
D
A
O
∵四边形ABCD是平行四边形,
∴OA=OC,
∵△AOB与△BOC的边OA,OC上的高相同,
∴S△AOB=S△BOC.
同理可得 S△BOC=S△COD,S△COD=S△DOA,
S△DOA= S△AOB
故S△AOB=S△BOC=S△COD=S△DOA.
知识点拨:
平行四边形的对角线分平
行四边形为四个面积相等
的三角形,且都等于平行
四边形面积的四分之一.
解:公平,理由如下(方法不唯一):
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.平行四边形的性质
2.平行四边形的性质的综合应用
解决求线段,周长、求证边、角关系等问题
第十八章 平行四边形
18.1.1 平行四边形的性质
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解平行四边形对角线互相平分的性质.
2.综合运用平行四边形的性质进行有关的论证和计算.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解平行四边形对角线互相平分的性质
活动:根据定义画出一个平行四边形ABCD,连接AC、BD,并设它们相交于
点O,量一量OA、OC、OB、OD的长度,你有什么猜想呢 用所学知识论证你的结论.
A
B
D
C
O
OA=OC,OB=OD
猜想:
平行四边形的对角线互相平分.
活动探究
学习目标
当堂检测
课堂总结
已知:如图,□ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC,
∴ ∠1=∠2,∠3=∠4,
∴ △AOD≌△COB(ASA),
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
新知生成
平行四边形的对角线互相平分.
活动探究
学习目标
当堂检测
课堂总结
活动:请解决下列问题.(要求:写出解答过程,
小组归纳做题时遇到的问题、用到的性质或方法)
(1)如图1,在 ABCD中,对角线AC、BD相交于点E,
AC⊥BC.若AC=4, AB=5,求BD的长、 ABCD的面积.
(2)如图2, ABCD的对角线AC,BD交于点O.EF过点O
且与AB,CD分别相交于点E,F.求证:OE=OF.
任务二:综合运用平行四边形的性质进行有关的论证和计算
图1
图2
A
B
C
D
F
E
O
活动探究
学习目标
当堂检测
课堂总结
(1)如图1,在 ABCD中,对角线AC、BD相交于点E,AC⊥BC.若AC=4,AB=5,
求出BD的长、 ABCD的面积.
解:(1)∵四边形ABCD是平行四边形,
∵AC⊥BC,
∴△ACB是直角三角形,
∴CE= AC,BE= BD,
根据勾股定理,BC=
∵CE= AC=2,
∴BE=
∴BD=2BE= ,
∴S ABCD= BC·AC= 3×4=12.
图1
活动探究
学习目标
当堂检测
课堂总结
(2)如图2, ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.
求证:OE=OF.
图2
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD, OD=OB,
∴OE=OF.
活动探究
学习目标
当堂检测
课堂总结
活动小结
勾股定理与判定三角形全等是解决平行四边形中线段的计算或证明边、角
关系的的重要方法,要注意结合图形灵活运用平行四边形的性质,如对边平行
且相等、对角相等、两邻角互补、对角线互相平分,先找出边、角的关系,再
进行相关计算或证明.
活动探究
学习目标
当堂检测
课堂总结
练一练
如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则BD的长是 .
1.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OBC的周长为 ( )
A.26 B.34
C.40 D.52
B
2.如图,在 ABCD中,∠ODA=90°,AC=10,BD=6,则AD的长为 .
4
3.如图,在平行四边形ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
BE=DF,BE∥DF.
∴BE∥DF.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
∴OE=OF.
在△EOB和△FOD中
∴△EOB≌△FOD,
∴BE=DF,∠FDB=∠EBD,
∴BE=DF,BE∥DF.
4.一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了
一块平行四边形的土地,由于年迈体弱,他决定按照如下方法将这块土地分给
他的四个孩子,他的分法是否公平,请通过计算说明.
老大
老二
老三
老四
B
C
D
A
O
∵四边形ABCD是平行四边形,
∴OA=OC,
∵△AOB与△BOC的边OA,OC上的高相同,
∴S△AOB=S△BOC.
同理可得 S△BOC=S△COD,S△COD=S△DOA,
S△DOA= S△AOB
故S△AOB=S△BOC=S△COD=S△DOA.
知识点拨:
平行四边形的对角线分平
行四边形为四个面积相等
的三角形,且都等于平行
四边形面积的四分之一.
解:公平,理由如下(方法不唯一):
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.平行四边形的性质
2.平行四边形的性质的综合应用
解决求线段,周长、求证边、角关系等问题
