2023-2024学年初中数学人教版八年级下册17.1 勾股定理 第1课时课件(共18张PPT)
文档属性
| 名称 | 2023-2024学年初中数学人教版八年级下册17.1 勾股定理 第1课时课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 11:51:26 | ||
图片预览



文档简介
(共18张PPT)
第十七章 勾股定理
17.1 勾股定理
第1课时
活动探究
学习目标
当堂检测
课堂总结
1.经历探究勾股定理的过程,掌握勾股定理的证明.
2.会用勾股定理进行简单的计算.
活动探究
学习目标
当堂检测
课堂总结
任务一:探索勾股定理,掌握勾股定理的证明
活动1:阅读材料,尝试解答下列三个问题,简要说说你的方法.
相传2500多年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
(1)观察发现正方形A、B、C的面积之间满足数量关系:
.
A
B
C
(2)三个正方形中间的等腰直角三角形的三边
之间满足数量关系:
.
S正方形A + S正方形B = S正方形C
一直角边2 +另一直角边2 =斜边2
活动探究
学习目标
当堂检测
课堂总结
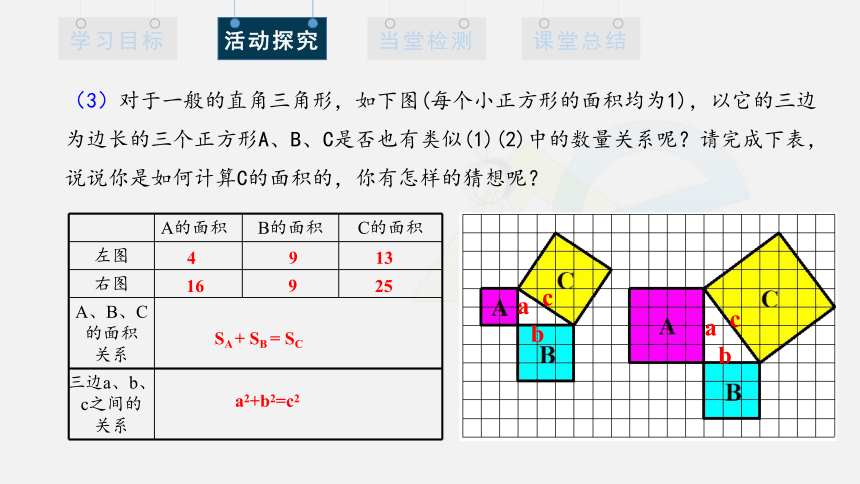
(3)对于一般的直角三角形,如下图(每个小正方形的面积均为1),以它的三边为边长的三个正方形A、B、C是否也有类似(1)(2)中的数量关系呢?请完成下表,说说你是如何计算C的面积的,你有怎样的猜想呢?
A的面积 B的面积 C的面积
左图
右图
A、B、C 的面积
关系
三边a、b、c之间的
关系
a
b
c
a
b
c
16
9
25
4
9
13
SA + SB = SC
a2+b2=c2
活动探究
学习目标
当堂检测
课堂总结
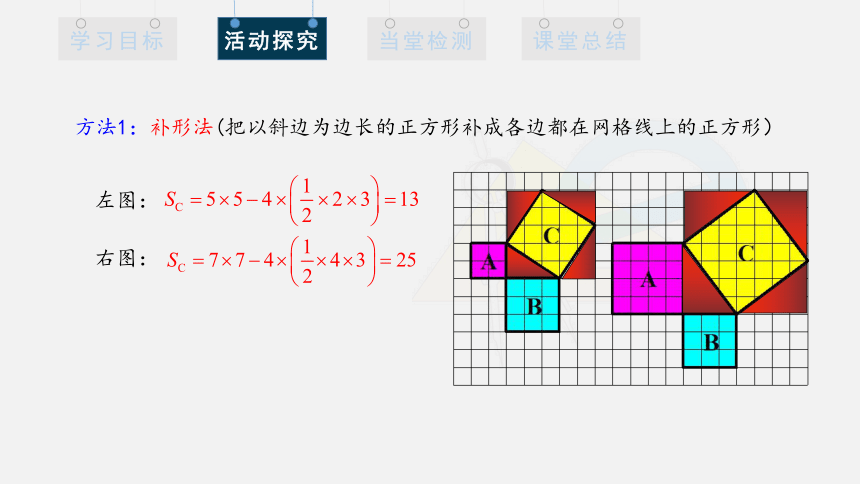
方法1:补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形)
左图:
右图:
活动探究
学习目标
当堂检测
课堂总结
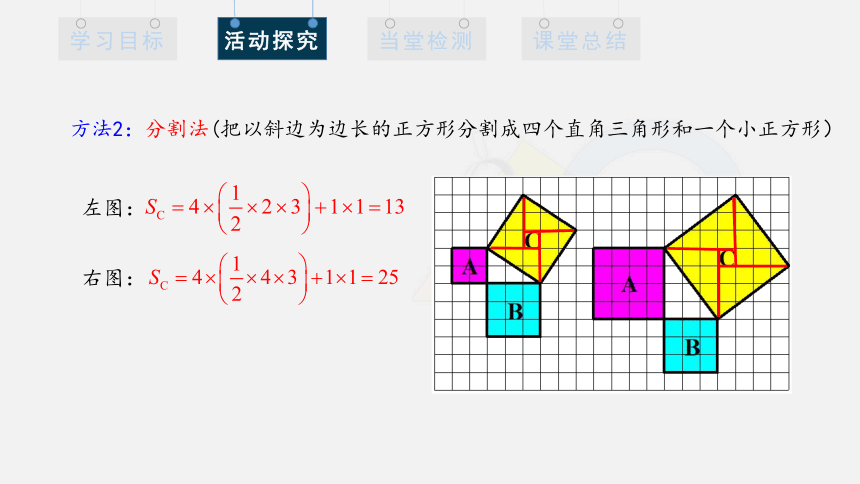
方法2:分割法(把以斜边为边长的正方形分割成四个直角三角形和一个小正方形)
左图:
右图:
活动探究
学习目标
当堂检测
课堂总结
A
B
C
a
b
c
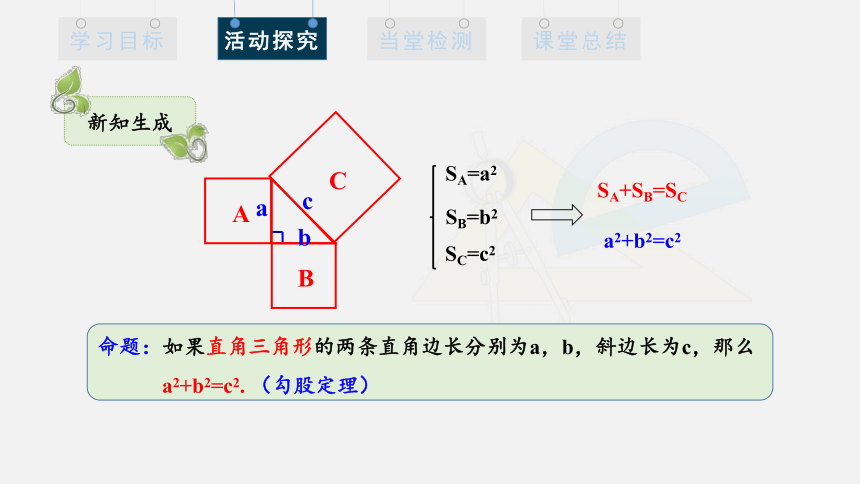
SA=a2
SB=b2
SC=c2
a2+b2=c2
SA+SB=SC
命题:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么
a2+b2=c2. (勾股定理)
新知生成
活动探究
学习目标
当堂检测
课堂总结
活动2:结合教材23-24页的内容,观察下面“赵爽弦图”的形成过程,尝试用所拼成的图形证明勾股定理.
b
b
c
a
b
c
a
a
活动探究
学习目标
当堂检测
课堂总结
a
b
c
b-a
赵爽弦图
证明:
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4S直角三角形+S小正方形,
即 直角三角形的两直角边的平方和等于斜边的平方.
活动探究
学习目标
当堂检测
课堂总结
练一练
1.以一个直角三角形的三边为边向外部作三个正方形,最大的正方形的面积
为25,则两个较小的正方形的面积之和为 .
4
2.如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个正方形的面积分别为26和10,则正方形A的边长是 .
25
活动探究
学习目标
当堂检测
课堂总结
活动:比一比,看谁做的又对又快!(要求:简要写出解答过程,小组讨论、归纳在解答过程遇到的问题或注意事项,整理提交.)
任务二:利用勾股定理进行计算
(2)在Rt△ABC中,若a=3,c=5,求b.
(1)如图1,在Rt△ABC中,∠C=90°.若a=b=5,求c;
C
A
B
图1
活动探究
学习目标
当堂检测
课堂总结
(2)当b是直角边时,由勾股定理得,
当b是斜边时,由勾股定理得,
所以b的值是4或 .
解:
(1)根据勾股定理得,
C
A
B
图1
活动探究
学习目标
当堂检测
课堂总结
在直角三角形中,当已知其任意两边长,可利用勾股定理求第三边长.一般先确定哪个角是直角、明确直角边和斜边,再利用勾股定理实现边的转化.(数形结合)
活动小结
a
b
c
常用公式:
(a、b、c为正数)
活动探究
学习目标
当堂检测
课堂总结
练一练
在Rt△ABC中,∠C=90°,如果a=5,c=13,求b的值.
解:由勾股定理得,
所以b的值是12.
1.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
2.在△ABC中,∠C=90°.
(1)若a=6,b=8,则c= .
(2)若c=13,b=12,则a= .
10
5
3.用两个完全相同的直角三角形(直角边为a、b,斜边为c,点B、C、E在同一直线上)构成如图所示的梯形.
b
a+b
下底
(1)填空:如图,梯形的上底为a,下底为 ,
高为 .
所以梯形的面积= ×(上底+ )×高= ×(a+ )×( ).
b
a+b
由“梯形面积等于三个直角三角形面积之和”可得梯形的面积为:
.
(2)利用此梯形面积的两种不同的求法来证明勾股定理.
解:
∴
即
针对本课的关键词“勾股定理”,你能说一说你都学到了哪些知识吗?
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2
证明
赵爽利用“弦图”,通过切割、拼接的
方法,以面积为等量关系,证明勾股定理
计算
确定直角,利用勾股定理实现边的转化
第十七章 勾股定理
17.1 勾股定理
第1课时
活动探究
学习目标
当堂检测
课堂总结
1.经历探究勾股定理的过程,掌握勾股定理的证明.
2.会用勾股定理进行简单的计算.
活动探究
学习目标
当堂检测
课堂总结
任务一:探索勾股定理,掌握勾股定理的证明
活动1:阅读材料,尝试解答下列三个问题,简要说说你的方法.
相传2500多年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
(1)观察发现正方形A、B、C的面积之间满足数量关系:
.
A
B
C
(2)三个正方形中间的等腰直角三角形的三边
之间满足数量关系:
.
S正方形A + S正方形B = S正方形C
一直角边2 +另一直角边2 =斜边2
活动探究
学习目标
当堂检测
课堂总结
(3)对于一般的直角三角形,如下图(每个小正方形的面积均为1),以它的三边为边长的三个正方形A、B、C是否也有类似(1)(2)中的数量关系呢?请完成下表,说说你是如何计算C的面积的,你有怎样的猜想呢?
A的面积 B的面积 C的面积
左图
右图
A、B、C 的面积
关系
三边a、b、c之间的
关系
a
b
c
a
b
c
16
9
25
4
9
13
SA + SB = SC
a2+b2=c2
活动探究
学习目标
当堂检测
课堂总结
方法1:补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形)
左图:
右图:
活动探究
学习目标
当堂检测
课堂总结
方法2:分割法(把以斜边为边长的正方形分割成四个直角三角形和一个小正方形)
左图:
右图:
活动探究
学习目标
当堂检测
课堂总结
A
B
C
a
b
c
SA=a2
SB=b2
SC=c2
a2+b2=c2
SA+SB=SC
命题:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么
a2+b2=c2. (勾股定理)
新知生成
活动探究
学习目标
当堂检测
课堂总结
活动2:结合教材23-24页的内容,观察下面“赵爽弦图”的形成过程,尝试用所拼成的图形证明勾股定理.
b
b
c
a
b
c
a
a
活动探究
学习目标
当堂检测
课堂总结
a
b
c
b-a
赵爽弦图
证明:
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4S直角三角形+S小正方形,
即 直角三角形的两直角边的平方和等于斜边的平方.
活动探究
学习目标
当堂检测
课堂总结
练一练
1.以一个直角三角形的三边为边向外部作三个正方形,最大的正方形的面积
为25,则两个较小的正方形的面积之和为 .
4
2.如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个正方形的面积分别为26和10,则正方形A的边长是 .
25
活动探究
学习目标
当堂检测
课堂总结
活动:比一比,看谁做的又对又快!(要求:简要写出解答过程,小组讨论、归纳在解答过程遇到的问题或注意事项,整理提交.)
任务二:利用勾股定理进行计算
(2)在Rt△ABC中,若a=3,c=5,求b.
(1)如图1,在Rt△ABC中,∠C=90°.若a=b=5,求c;
C
A
B
图1
活动探究
学习目标
当堂检测
课堂总结
(2)当b是直角边时,由勾股定理得,
当b是斜边时,由勾股定理得,
所以b的值是4或 .
解:
(1)根据勾股定理得,
C
A
B
图1
活动探究
学习目标
当堂检测
课堂总结
在直角三角形中,当已知其任意两边长,可利用勾股定理求第三边长.一般先确定哪个角是直角、明确直角边和斜边,再利用勾股定理实现边的转化.(数形结合)
活动小结
a
b
c
常用公式:
(a、b、c为正数)
活动探究
学习目标
当堂检测
课堂总结
练一练
在Rt△ABC中,∠C=90°,如果a=5,c=13,求b的值.
解:由勾股定理得,
所以b的值是12.
1.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
2.在△ABC中,∠C=90°.
(1)若a=6,b=8,则c= .
(2)若c=13,b=12,则a= .
10
5
3.用两个完全相同的直角三角形(直角边为a、b,斜边为c,点B、C、E在同一直线上)构成如图所示的梯形.
b
a+b
下底
(1)填空:如图,梯形的上底为a,下底为 ,
高为 .
所以梯形的面积= ×(上底+ )×高= ×(a+ )×( ).
b
a+b
由“梯形面积等于三个直角三角形面积之和”可得梯形的面积为:
.
(2)利用此梯形面积的两种不同的求法来证明勾股定理.
解:
∴
即
针对本课的关键词“勾股定理”,你能说一说你都学到了哪些知识吗?
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2
证明
赵爽利用“弦图”,通过切割、拼接的
方法,以面积为等量关系,证明勾股定理
计算
确定直角,利用勾股定理实现边的转化
