18.2.1 矩形 第2课时 课件(共14张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 18.2.1 矩形 第2课时 课件(共14张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 16:45:01 | ||
图片预览





文档简介
(共14张PPT)
第十八章 平行四边形
18.2.1 矩形
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解并掌握矩形的判定方法,会用矩形定义及判定定理判定一个
四边形是否为矩形.
2.能综合应用矩形的判定及性质进行有关计算与论证.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解并掌握矩形的判定方法,会判定一个四边形是否为矩形.
活动1:小组合作完成下列问题,整理归纳矩形的判定方法.
情境:小华用两根长度相等的短木板和两根长度相等的长木板,做了一个矩形
像框(如图所示),有什么办法可以检测这个像框是矩形呢?
(1)结合所学的矩形、平行四边形的知识,说说你的方法.
(2)若该相框的四个角都是直角,能否说明它是矩形?至少
要满足几个角是直角呢?(画图说明)
(3)结合(1)(2)写出你的猜想,并进行证明.
活动探究
学习目标
当堂检测
课堂总结
定义法:有一个角是直角的平行四边形是矩形.
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
对角线相等的平行四边形是矩形.
猜想1:
有三个角是直角的四边形是矩形.
猜想2:
活动探究
学习目标
当堂检测
课堂总结
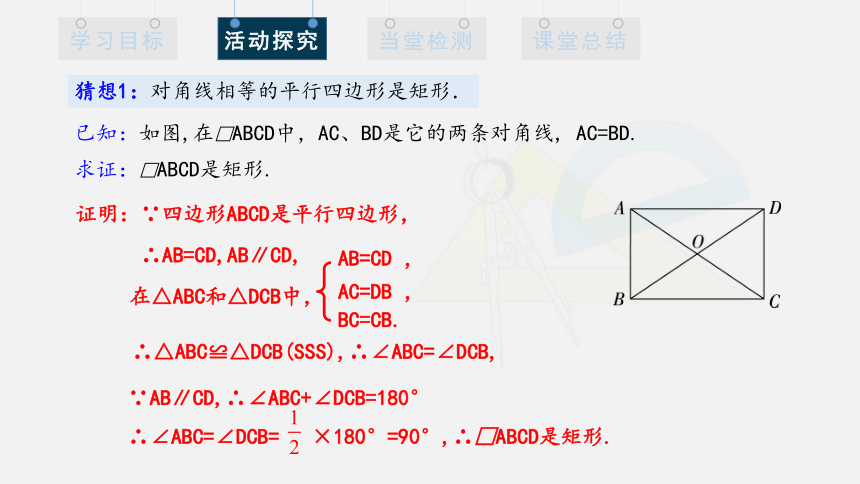
已知:如图,在□ABCD中,AC、BD是它的两条对角线, AC=BD.
求证:□ABCD是矩形.
猜想1:对角线相等的平行四边形是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
在△ABC和△DCB中,
AB=CD ,
BC=CB.
AC=DB ,
∴△ABC≌△DCB(SSS),∴∠ABC=∠DCB,
∵AB∥CD,∴∠ABC+∠DCB=180°
∴∠ABC=∠DCB= ×180°=90°,∴□ABCD是矩形.
活动探究
学习目标
当堂检测
课堂总结
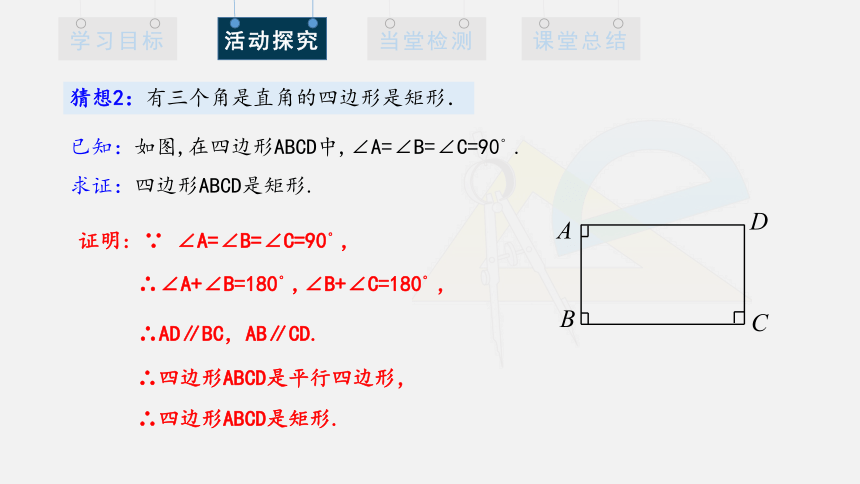
猜想2:有三个角是直角的四边形是矩形.
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
证明: ∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
活动探究
学习目标
当堂检测
课堂总结
活动小结
矩形的判定方法:
(1)定义法:有一个角是直角的平行四边形是矩形.
(2)判定定理:对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
基本思路: ①是平行四边形,并且有一个是直角→矩形
②是平行四边形,并且两条对角线相等→矩形
③四边形,有三个角是直角→矩形
活动探究
学习目标
当堂检测
课堂总结
活动2:下列判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形; ( )
(2)有四个角是直角的四边形是矩形; ( )
(3)四个角都相等的四边形是矩形; ( )
(4)对角线相等的四边形是矩形; ( )
(5)对角线互相平分且相等的四边形是矩形; ( )
(6)对角线相等,且有一个角是直角的四边形是矩形; ( )
(7)一组邻边垂直,一组对边平行且相等的四边形是矩形; ( )
(8)两组对边分别平行,且对角线相等的四边形是矩形. ( )
×
×
√
√
√
×
√
√
活动探究
学习目标
当堂检测
课堂总结
任务二:掌握矩形的判定及性质的综合应用.
活动:如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.
求∠OAB的度数.(要求:写出解答过程,简要说说你用到了哪些的性质或方法)
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,
OB=OD= BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
活动探究
学习目标
当堂检测
课堂总结
练一练
如图,已知在四边形ABCD中,AB=DC,AD=BC,连接AC,BD,AC与BD交于点O,若AO=BO,AD=3,AB=2,求四边形ABCD的面积.
解:∵AB=DC,AD=BC,
∴四边形ABCD为平行四边形,
∴AO=OC,BO=DO,
∵AO=BO,
∴AC=BD,
∴四边形ABCD为矩形,
∵AD=3,AB=2,
∴四边形ABCD的面积为:AD AB=2×3=6.
1.在判断“一个四边形门框是否为矩形”的数学活动课上,一个合作学习小组的4位同学分别拟定了如下的方案,其中正确的是( )
A.测量对角线是否相等
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量其中三个角是否都为直角
D
2.如图,□ ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠DAB+∠ABC=180°.
∵AH,BH分别平分∠DAB与∠ABC.
∴∠HAB= ∠DAB,∠HBA= ∠ABC.
∴∠HAB+∠HBA= (∠DAB+∠ABC) =90°.
∴∠H=90°,同理∠HEF=∠F=90°,
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
3.已知□ ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,
求这个平行四边形的面积.
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,
OB=OD= BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
在Rt△ABC中,
∵AB=4cm,AC=2AO=8cm,
∴BC= (cm).
∴S□ ABCD=AB·BC= 4×4 (cm2).
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.矩形的判定方法
2.矩形的判定定理及性质的综合运用
计算与论证
第十八章 平行四边形
18.2.1 矩形
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解并掌握矩形的判定方法,会用矩形定义及判定定理判定一个
四边形是否为矩形.
2.能综合应用矩形的判定及性质进行有关计算与论证.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解并掌握矩形的判定方法,会判定一个四边形是否为矩形.
活动1:小组合作完成下列问题,整理归纳矩形的判定方法.
情境:小华用两根长度相等的短木板和两根长度相等的长木板,做了一个矩形
像框(如图所示),有什么办法可以检测这个像框是矩形呢?
(1)结合所学的矩形、平行四边形的知识,说说你的方法.
(2)若该相框的四个角都是直角,能否说明它是矩形?至少
要满足几个角是直角呢?(画图说明)
(3)结合(1)(2)写出你的猜想,并进行证明.
活动探究
学习目标
当堂检测
课堂总结
定义法:有一个角是直角的平行四边形是矩形.
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
对角线相等的平行四边形是矩形.
猜想1:
有三个角是直角的四边形是矩形.
猜想2:
活动探究
学习目标
当堂检测
课堂总结
已知:如图,在□ABCD中,AC、BD是它的两条对角线, AC=BD.
求证:□ABCD是矩形.
猜想1:对角线相等的平行四边形是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
在△ABC和△DCB中,
AB=CD ,
BC=CB.
AC=DB ,
∴△ABC≌△DCB(SSS),∴∠ABC=∠DCB,
∵AB∥CD,∴∠ABC+∠DCB=180°
∴∠ABC=∠DCB= ×180°=90°,∴□ABCD是矩形.
活动探究
学习目标
当堂检测
课堂总结
猜想2:有三个角是直角的四边形是矩形.
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
证明: ∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
活动探究
学习目标
当堂检测
课堂总结
活动小结
矩形的判定方法:
(1)定义法:有一个角是直角的平行四边形是矩形.
(2)判定定理:对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
基本思路: ①是平行四边形,并且有一个是直角→矩形
②是平行四边形,并且两条对角线相等→矩形
③四边形,有三个角是直角→矩形
活动探究
学习目标
当堂检测
课堂总结
活动2:下列判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形; ( )
(2)有四个角是直角的四边形是矩形; ( )
(3)四个角都相等的四边形是矩形; ( )
(4)对角线相等的四边形是矩形; ( )
(5)对角线互相平分且相等的四边形是矩形; ( )
(6)对角线相等,且有一个角是直角的四边形是矩形; ( )
(7)一组邻边垂直,一组对边平行且相等的四边形是矩形; ( )
(8)两组对边分别平行,且对角线相等的四边形是矩形. ( )
×
×
√
√
√
×
√
√
活动探究
学习目标
当堂检测
课堂总结
任务二:掌握矩形的判定及性质的综合应用.
活动:如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.
求∠OAB的度数.(要求:写出解答过程,简要说说你用到了哪些的性质或方法)
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,
OB=OD= BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
活动探究
学习目标
当堂检测
课堂总结
练一练
如图,已知在四边形ABCD中,AB=DC,AD=BC,连接AC,BD,AC与BD交于点O,若AO=BO,AD=3,AB=2,求四边形ABCD的面积.
解:∵AB=DC,AD=BC,
∴四边形ABCD为平行四边形,
∴AO=OC,BO=DO,
∵AO=BO,
∴AC=BD,
∴四边形ABCD为矩形,
∵AD=3,AB=2,
∴四边形ABCD的面积为:AD AB=2×3=6.
1.在判断“一个四边形门框是否为矩形”的数学活动课上,一个合作学习小组的4位同学分别拟定了如下的方案,其中正确的是( )
A.测量对角线是否相等
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量其中三个角是否都为直角
D
2.如图,□ ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠DAB+∠ABC=180°.
∵AH,BH分别平分∠DAB与∠ABC.
∴∠HAB= ∠DAB,∠HBA= ∠ABC.
∴∠HAB+∠HBA= (∠DAB+∠ABC) =90°.
∴∠H=90°,同理∠HEF=∠F=90°,
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
3.已知□ ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,
求这个平行四边形的面积.
解:∵四边形ABCD是平行四边形,
∴OA=OC= AC,
OB=OD= BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
在Rt△ABC中,
∵AB=4cm,AC=2AO=8cm,
∴BC= (cm).
∴S□ ABCD=AB·BC= 4×4 (cm2).
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.矩形的判定方法
2.矩形的判定定理及性质的综合运用
计算与论证
