18.2.2 菱形 第2课时 课件(共16张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 18.2.2 菱形 第2课时 课件(共16张PPT) 2023-2024学年初中数学人教版八年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 11:54:57 | ||
图片预览




文档简介
(共16张PPT)
第十八章 平行四边形
18.2.2 菱形
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解并掌握菱形的定义及其它两个判定方法.
2.运用菱形的判定方法进行有关的论证和计算.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解并掌握菱形的定义及其它两个判定方法.
活动1:请解决下列问题,整理归纳菱形的判定方法.
(1)运用菱形的定义进行菱形的判定,应具备哪几个条件?
(2)菱形的性质定理有哪些?写出它们所对应的逆命题,判断这些逆命题
是否成立.(写出已知、求证、画出图形并证明)
1.对角线互相垂直的平行四边形是菱形.
2.四条边相等的四边形是菱形.
逆命题:
定义:有一组邻边相等的平行四边形是菱形.
活动探究
学习目标
当堂检测
课堂总结
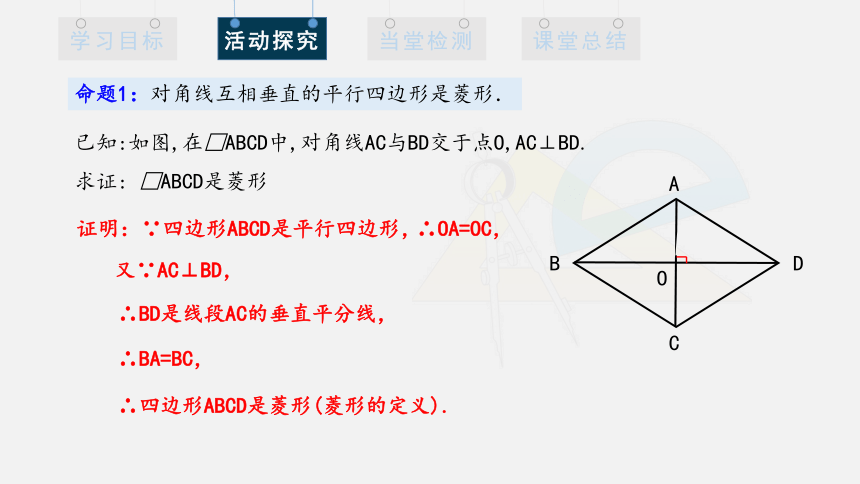
命题1:对角线互相垂直的平行四边形是菱形.
已知:如图,在□ABCD中,对角线AC与BD交于点O,AC⊥BD.
求证: □ABCD是菱形
证明:∵四边形ABCD是平行四边形,
∴OA=OC,
又∵AC⊥BD,
∴BD是线段AC的垂直平分线,
∴BA=BC,
∴四边形ABCD是菱形(菱形的定义).
A
B
C
D
O
活动探究
学习目标
当堂检测
课堂总结
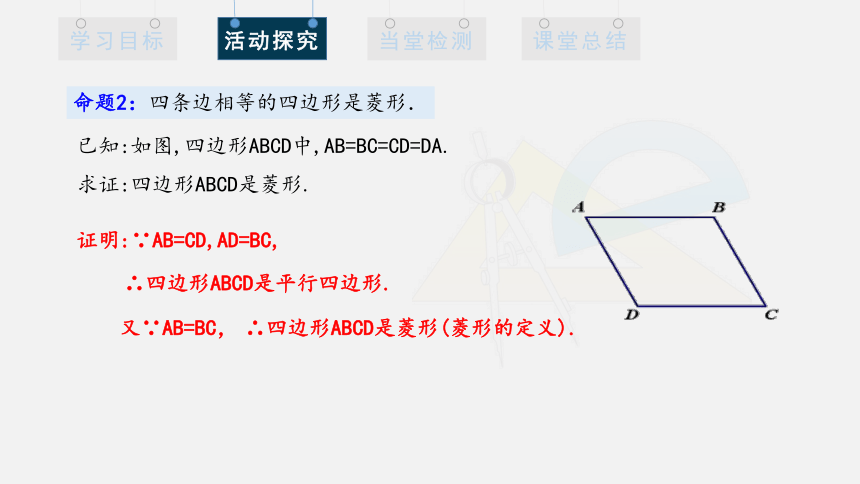
命题2:四条边相等的四边形是菱形.
已知:如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形(菱形的定义).
活动探究
学习目标
当堂检测
课堂总结
活动小结
菱形的判定方法如下:
(2)判定定理:
对角线互相垂直的平行四边形是菱形.
四条边相等的四边形是菱形.
有一组邻边相等的平行四边形是菱形.
(1)定义法:
活动探究
学习目标
当堂检测
课堂总结
练一练
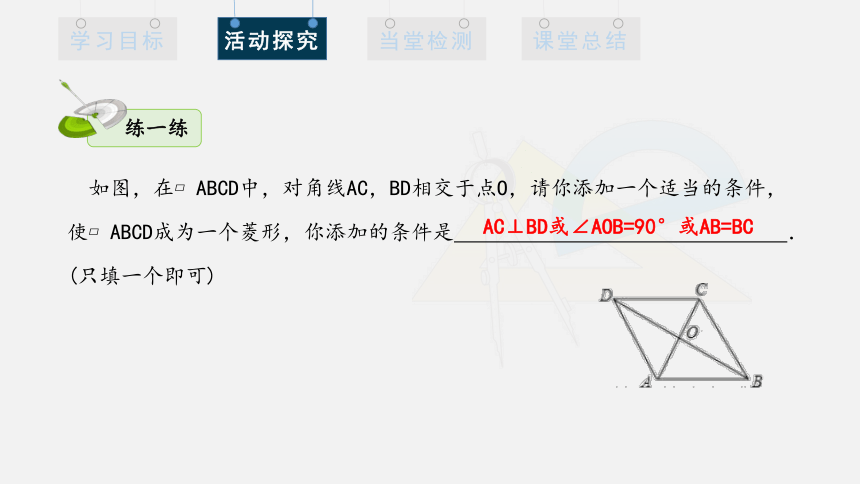
如图,在 ABCD中,对角线AC,BD相交于点O,请你添加一个适当的条件,
使 ABCD成为一个菱形,你添加的条件是 .
(只填一个即可)
AC⊥BD或∠AOB=90°或AB=BC
活动探究
学习目标
当堂检测
课堂总结
任务二:运用菱形的判定方法进行有关的论证和计算.
活动:请解答下列问题.(要求:简要说说证明或求解
的思路,小组整理归纳求解过程中用到的性质和方法)
(1)如图1, ABCD的两条对角线AC,BD相交于点O,
AB=5,AC=8,DB=6.求证:四边形ABCD是菱形.
(2)如图2,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,求∠AOF的度数.
图1
图2
活动探究
学习目标
当堂检测
课堂总结
(1)如图1, ABCD的两条对角线AC,BD相交于点O,AB=5,AC=8,DB=6.求证:四边形ABCD是菱形.
A
B
C
D
O
证明:∵四边形ABCD是平行四边形,
∴OA=OC=4,OB=OD=3.
又∵AB=5,则32+42=52,即OA2+OB2=AB2,
∴∠AOB=90°,即AC⊥BD,
∴四边形ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)
活动探究
学习目标
当堂检测
课堂总结
(2)如图2,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD
交EF于O,求∠AOF的度数.
图2
解:∵DE∥AC,DF∥AB,∴四边形AEDF为平行四边形,
∴OA=OD,OE=OF,∠2=∠3,
∵AD是△ABC的角平分线,∠1=∠2,
∴∠1=∠3,∴AE=DE
∴ AEDF为菱形 (菱形的定义),
∴AD⊥EF,即∠AOF=90°
活动探究
学习目标
当堂检测
课堂总结
活动小结
判定菱形的一般思路:
当涉及菱形的论证和计算时,要根据已知条件灵活选择判定方法,结合等腰
三角形、直角三角形的相关性质,三角形的全等判定等进行计算或证明.
活动探究
学习目标
当堂检测
课堂总结
练一练
一个平行四边形的一条边长是9,两条对角线的长分别是12和6,这是一个
特殊的平行四边形吗?为什么?求出它的面积.
解:∵平行四边形的两条对角线的长分别是12和 ,
∴两条对角线的长的一半分别是6和 ,
∵62+( )2=81=92,
∴两对角线的一半与边长构成的三角形是直角三角形,
∴此平行四边形是菱形,面积= ×12 × = .
1.如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD是否
是一个菱形 (填“是”或“不是”),理由是:
.
四边相等的四边形是菱形
是
2.如图,在 ABCD中,AC平分∠DAB,AB=2,求 ABCD的周长.
解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,
又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACB=∠BAC,
∴平行四边形ABCD为菱形,
又∵AB=2,
∴AD∥BC,
∴AB=BC,
∴四边形ABCD的周长=4×2=8.
3.已知:如图, ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
证明:∵四边形ABCD是平行四边形,
∴AE∥FC,∴∠EAC=∠FCA.
又∠AOE=∠COF,AO=CO,
∴△AOE≌△COF(ASA).∴EO=FO.
∴四边形AFCE是平行四边形.
又EF⊥AC,
∴AFCE是菱形(对角线互相垂直的平行四边形是菱形).
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.菱形的判定方法
2.菱形的判定方法的运用
计算与论证
第十八章 平行四边形
18.2.2 菱形
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解并掌握菱形的定义及其它两个判定方法.
2.运用菱形的判定方法进行有关的论证和计算.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解并掌握菱形的定义及其它两个判定方法.
活动1:请解决下列问题,整理归纳菱形的判定方法.
(1)运用菱形的定义进行菱形的判定,应具备哪几个条件?
(2)菱形的性质定理有哪些?写出它们所对应的逆命题,判断这些逆命题
是否成立.(写出已知、求证、画出图形并证明)
1.对角线互相垂直的平行四边形是菱形.
2.四条边相等的四边形是菱形.
逆命题:
定义:有一组邻边相等的平行四边形是菱形.
活动探究
学习目标
当堂检测
课堂总结
命题1:对角线互相垂直的平行四边形是菱形.
已知:如图,在□ABCD中,对角线AC与BD交于点O,AC⊥BD.
求证: □ABCD是菱形
证明:∵四边形ABCD是平行四边形,
∴OA=OC,
又∵AC⊥BD,
∴BD是线段AC的垂直平分线,
∴BA=BC,
∴四边形ABCD是菱形(菱形的定义).
A
B
C
D
O
活动探究
学习目标
当堂检测
课堂总结
命题2:四条边相等的四边形是菱形.
已知:如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形(菱形的定义).
活动探究
学习目标
当堂检测
课堂总结
活动小结
菱形的判定方法如下:
(2)判定定理:
对角线互相垂直的平行四边形是菱形.
四条边相等的四边形是菱形.
有一组邻边相等的平行四边形是菱形.
(1)定义法:
活动探究
学习目标
当堂检测
课堂总结
练一练
如图,在 ABCD中,对角线AC,BD相交于点O,请你添加一个适当的条件,
使 ABCD成为一个菱形,你添加的条件是 .
(只填一个即可)
AC⊥BD或∠AOB=90°或AB=BC
活动探究
学习目标
当堂检测
课堂总结
任务二:运用菱形的判定方法进行有关的论证和计算.
活动:请解答下列问题.(要求:简要说说证明或求解
的思路,小组整理归纳求解过程中用到的性质和方法)
(1)如图1, ABCD的两条对角线AC,BD相交于点O,
AB=5,AC=8,DB=6.求证:四边形ABCD是菱形.
(2)如图2,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,求∠AOF的度数.
图1
图2
活动探究
学习目标
当堂检测
课堂总结
(1)如图1, ABCD的两条对角线AC,BD相交于点O,AB=5,AC=8,DB=6.求证:四边形ABCD是菱形.
A
B
C
D
O
证明:∵四边形ABCD是平行四边形,
∴OA=OC=4,OB=OD=3.
又∵AB=5,则32+42=52,即OA2+OB2=AB2,
∴∠AOB=90°,即AC⊥BD,
∴四边形ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)
活动探究
学习目标
当堂检测
课堂总结
(2)如图2,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD
交EF于O,求∠AOF的度数.
图2
解:∵DE∥AC,DF∥AB,∴四边形AEDF为平行四边形,
∴OA=OD,OE=OF,∠2=∠3,
∵AD是△ABC的角平分线,∠1=∠2,
∴∠1=∠3,∴AE=DE
∴ AEDF为菱形 (菱形的定义),
∴AD⊥EF,即∠AOF=90°
活动探究
学习目标
当堂检测
课堂总结
活动小结
判定菱形的一般思路:
当涉及菱形的论证和计算时,要根据已知条件灵活选择判定方法,结合等腰
三角形、直角三角形的相关性质,三角形的全等判定等进行计算或证明.
活动探究
学习目标
当堂检测
课堂总结
练一练
一个平行四边形的一条边长是9,两条对角线的长分别是12和6,这是一个
特殊的平行四边形吗?为什么?求出它的面积.
解:∵平行四边形的两条对角线的长分别是12和 ,
∴两条对角线的长的一半分别是6和 ,
∵62+( )2=81=92,
∴两对角线的一半与边长构成的三角形是直角三角形,
∴此平行四边形是菱形,面积= ×12 × = .
1.如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD是否
是一个菱形 (填“是”或“不是”),理由是:
.
四边相等的四边形是菱形
是
2.如图,在 ABCD中,AC平分∠DAB,AB=2,求 ABCD的周长.
解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,
又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACB=∠BAC,
∴平行四边形ABCD为菱形,
又∵AB=2,
∴AD∥BC,
∴AB=BC,
∴四边形ABCD的周长=4×2=8.
3.已知:如图, ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
证明:∵四边形ABCD是平行四边形,
∴AE∥FC,∴∠EAC=∠FCA.
又∠AOE=∠COF,AO=CO,
∴△AOE≌△COF(ASA).∴EO=FO.
∴四边形AFCE是平行四边形.
又EF⊥AC,
∴AFCE是菱形(对角线互相垂直的平行四边形是菱形).
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.菱形的判定方法
2.菱形的判定方法的运用
计算与论证
