18.2.3 正方形课件 19张PPT 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 18.2.3 正方形课件 19张PPT 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
第十八章 平行四边形
18.2.3 正方形
活动探究
学习目标
当堂检测
课堂总结
1.理解正方形的概念、通过探索掌握正方形性质和判定方法.
2.理解正方形与平行四边形、矩形、菱形的关系.
3.能运用正方形性质和判定方法进行有关的证明和计算.
活动探究
学习目标
当堂检测
课堂总结
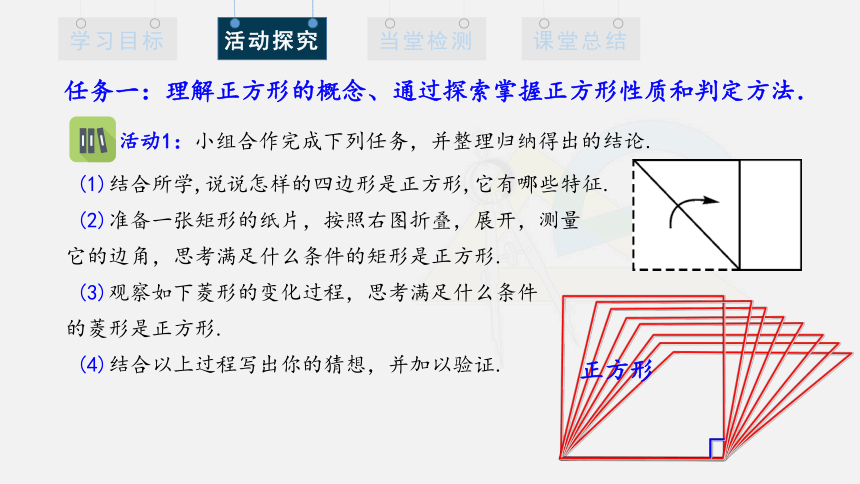
任务一:理解正方形的概念、通过探索掌握正方形性质和判定方法.
活动1:小组合作完成下列任务,并整理归纳得出的结论.
(1)结合所学,说说怎样的四边形是正方形,它有哪些特征.
(2)准备一张矩形的纸片,按照右图折叠,展开,测量
它的边角,思考满足什么条件的矩形是正方形.
(3)观察如下菱形的变化过程,思考满足什么条件
的菱形是正方形.
(4)结合以上过程写出你的猜想,并加以验证.
正方形
活动探究
学习目标
当堂检测
课堂总结
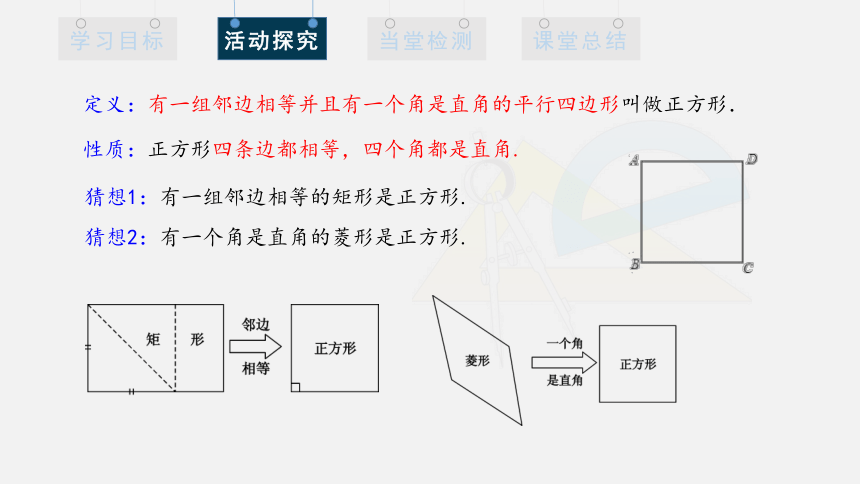
性质:正方形四条边都相等,四个角都是直角.
猜想1:有一组邻边相等的矩形是正方形.
猜想2:有一个角是直角的菱形是正方形.
定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
活动探究
学习目标
当堂检测
课堂总结
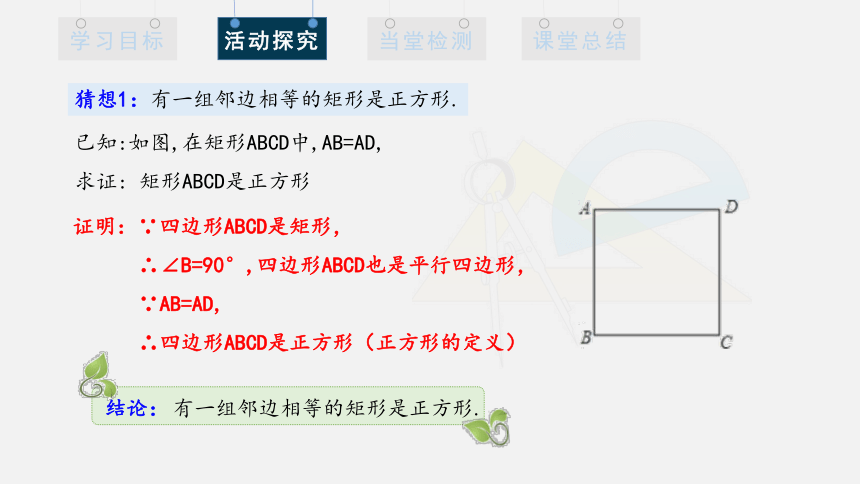
猜想1:有一组邻边相等的矩形是正方形.
已知:如图,在矩形ABCD中,AB=AD,
求证: 矩形ABCD是正方形
证明:∵四边形ABCD是矩形,
∴∠B=90°,四边形ABCD也是平行四边形,
∵AB=AD,
∴四边形ABCD是正方形(正方形的定义)
结论:
有一组邻边相等的矩形是正方形.
活动探究
学习目标
当堂检测
课堂总结
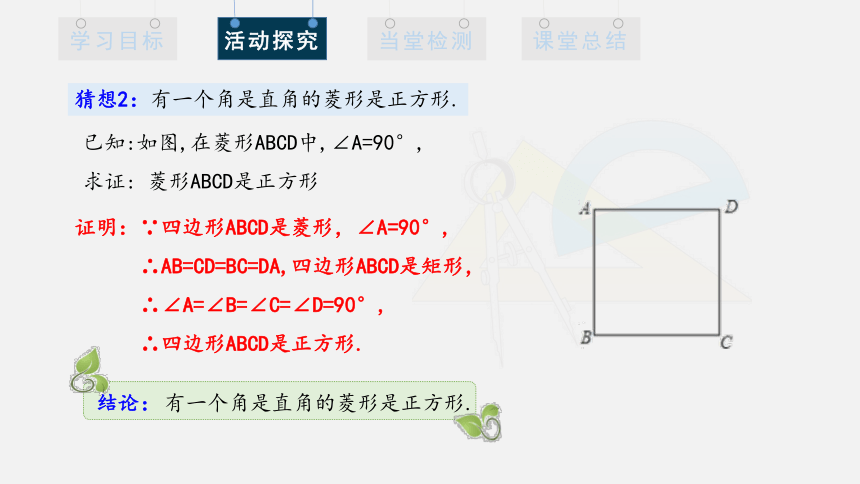
猜想2:有一个角是直角的菱形是正方形.
已知:如图,在菱形ABCD中,∠A=90°,
求证: 菱形ABCD是正方形
证明:∵四边形ABCD是菱形,∠A=90°,
∴AB=CD=BC=DA,四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD是正方形.
结论:
有一个角是直角的菱形是正方形.
活动探究
学习目标
当堂检测
课堂总结
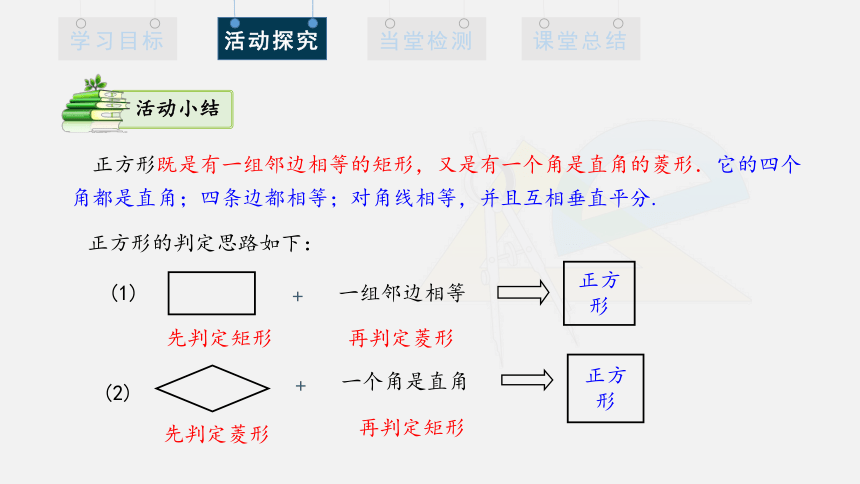
活动小结
正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.它的四个角都是直角;四条边都相等;对角线相等,并且互相垂直平分.
正方形
+
先判定菱形
再判定矩形
(2)
一个角是直角
正方形的判定思路如下:
正方形
+
先判定矩形
再判定菱形
(1)
一组邻边相等
活动探究
学习目标
当堂检测
课堂总结
思考
正方形是轴对称图形吗?若是,它的对称轴是什么?请画出它的所有对称轴.
正方形是轴对称图形,它有4条对称轴
(如图),分别是对边中点的连线以及两条对角线所在的直线.
活动探究
学习目标
当堂检测
课堂总结
活动2:与小组内同学讨论四边形、平行四边形、矩形、菱形、正方形的
从属关系,试完成下面的关系图.
四边形
平行四边形
菱形
矩形
正方形
活动探究
学习目标
当堂检测
课堂总结
1.菱形、矩形、正方形都具有的性质是( )
A.对角线相等且互相平分
B.对角线相等且垂直平分
C.对角线互相平分
D.四边相等,四个角相等
C
练一练
活动探究
学习目标
当堂检测
课堂总结
练一练
2.从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD,选两个作为补充条件,使 ABCD为正方形(如图).现有下列四种选法,其中错误的是( )
A.①② B.②③
C.①③ D.②④
B
活动探究
学习目标
当堂检测
课堂总结
任务二:能运用正方形性质和判定方法进行有关的证明和计算.
活动:小组合作解决下列问题,简要说说求解过程中用到的性质.
(1)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的
等腰直角三角形.
(2)右图中共有 个等腰直角三角形.
活动探究
学习目标
当堂检测
课堂总结
(1)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明:(1) ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形
∴△ABO≌ △BCO ≌ △CDO ≌ △DAO.
又∵ AD=CD=BC=AB
(2)右图中共有8个等腰直角三角形.
活动探究
学习目标
当堂检测
课堂总结
练一练
如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD= ,面积为AD2=8.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2,
D
1.下列命题中,正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线相等的菱形是正方形
2.如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
解:由題意知:EC=30m,EB=10m,
∴BC=302-102= ,
正方形的面积为( )2=800 m2,
对角线的长为 =40 m.
3.△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
证明:(1)∵点O为AB的中点,∴BO=AO,
又∵OE=OD,∴四边形AEBD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,∴∠ADB=90°,
∴平行四边形AEBD是矩形.
3.△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
(2)当∠BAC=90°时,矩形AEBD是正方形,理由如下:
∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD.
∵由(1)知四边形AEBD是矩形,
∴矩形AEBD是正方形.
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.正方形的定义及性质
2.正方形的判定方法
第十八章 平行四边形
18.2.3 正方形
活动探究
学习目标
当堂检测
课堂总结
1.理解正方形的概念、通过探索掌握正方形性质和判定方法.
2.理解正方形与平行四边形、矩形、菱形的关系.
3.能运用正方形性质和判定方法进行有关的证明和计算.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解正方形的概念、通过探索掌握正方形性质和判定方法.
活动1:小组合作完成下列任务,并整理归纳得出的结论.
(1)结合所学,说说怎样的四边形是正方形,它有哪些特征.
(2)准备一张矩形的纸片,按照右图折叠,展开,测量
它的边角,思考满足什么条件的矩形是正方形.
(3)观察如下菱形的变化过程,思考满足什么条件
的菱形是正方形.
(4)结合以上过程写出你的猜想,并加以验证.
正方形
活动探究
学习目标
当堂检测
课堂总结
性质:正方形四条边都相等,四个角都是直角.
猜想1:有一组邻边相等的矩形是正方形.
猜想2:有一个角是直角的菱形是正方形.
定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
活动探究
学习目标
当堂检测
课堂总结
猜想1:有一组邻边相等的矩形是正方形.
已知:如图,在矩形ABCD中,AB=AD,
求证: 矩形ABCD是正方形
证明:∵四边形ABCD是矩形,
∴∠B=90°,四边形ABCD也是平行四边形,
∵AB=AD,
∴四边形ABCD是正方形(正方形的定义)
结论:
有一组邻边相等的矩形是正方形.
活动探究
学习目标
当堂检测
课堂总结
猜想2:有一个角是直角的菱形是正方形.
已知:如图,在菱形ABCD中,∠A=90°,
求证: 菱形ABCD是正方形
证明:∵四边形ABCD是菱形,∠A=90°,
∴AB=CD=BC=DA,四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD是正方形.
结论:
有一个角是直角的菱形是正方形.
活动探究
学习目标
当堂检测
课堂总结
活动小结
正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.它的四个角都是直角;四条边都相等;对角线相等,并且互相垂直平分.
正方形
+
先判定菱形
再判定矩形
(2)
一个角是直角
正方形的判定思路如下:
正方形
+
先判定矩形
再判定菱形
(1)
一组邻边相等
活动探究
学习目标
当堂检测
课堂总结
思考
正方形是轴对称图形吗?若是,它的对称轴是什么?请画出它的所有对称轴.
正方形是轴对称图形,它有4条对称轴
(如图),分别是对边中点的连线以及两条对角线所在的直线.
活动探究
学习目标
当堂检测
课堂总结
活动2:与小组内同学讨论四边形、平行四边形、矩形、菱形、正方形的
从属关系,试完成下面的关系图.
四边形
平行四边形
菱形
矩形
正方形
活动探究
学习目标
当堂检测
课堂总结
1.菱形、矩形、正方形都具有的性质是( )
A.对角线相等且互相平分
B.对角线相等且垂直平分
C.对角线互相平分
D.四边相等,四个角相等
C
练一练
活动探究
学习目标
当堂检测
课堂总结
练一练
2.从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD,选两个作为补充条件,使 ABCD为正方形(如图).现有下列四种选法,其中错误的是( )
A.①② B.②③
C.①③ D.②④
B
活动探究
学习目标
当堂检测
课堂总结
任务二:能运用正方形性质和判定方法进行有关的证明和计算.
活动:小组合作解决下列问题,简要说说求解过程中用到的性质.
(1)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的
等腰直角三角形.
(2)右图中共有 个等腰直角三角形.
活动探究
学习目标
当堂检测
课堂总结
(1)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明:(1) ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形
∴△ABO≌ △BCO ≌ △CDO ≌ △DAO.
又∵ AD=CD=BC=AB
(2)右图中共有8个等腰直角三角形.
活动探究
学习目标
当堂检测
课堂总结
练一练
如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
在Rt△AOD中,由勾股定理,得
∴正方形的周长为4AD= ,面积为AD2=8.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2,
D
1.下列命题中,正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线相等的菱形是正方形
2.如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
解:由題意知:EC=30m,EB=10m,
∴BC=302-102= ,
正方形的面积为( )2=800 m2,
对角线的长为 =40 m.
3.△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
证明:(1)∵点O为AB的中点,∴BO=AO,
又∵OE=OD,∴四边形AEBD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,∴∠ADB=90°,
∴平行四边形AEBD是矩形.
3.△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
(2)当∠BAC=90°时,矩形AEBD是正方形,理由如下:
∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD.
∵由(1)知四边形AEBD是矩形,
∴矩形AEBD是正方形.
针对本课的以下关键词,你能说一说你都学到了哪些知识吗?
1.正方形的定义及性质
2.正方形的判定方法
