19.1.2 函数的图象 第2课时 课件(共16张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 19.1.2 函数的图象 第2课时 课件(共16张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第十九章 一次函数
19.1.2 函数的图象
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解函数的三种表示方法及其优缺点.
2.能用适当的方式表示实际问题中的变量之间的函数关系,解决与函数相关的简单问题.
活动探究
学习目标
当堂检测
课堂总结
任务一:结合具体实例,理解函数的三种表示方法及其优缺点.
活动1:请解决下列问题:
(1)阅读教材79页练习后的一段话,说一说表示函数的方法有哪些.
新知生成
表示函数的方法有以下三种:解析式法、列表法、图象法.它们分别
从数和形的角度反映了函数的本质.
活动探究
学习目标
当堂检测
课堂总结
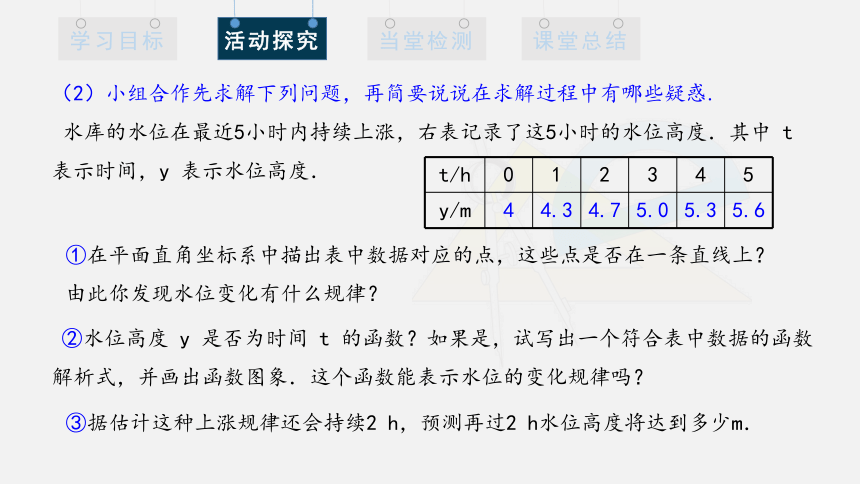
(2)小组合作先求解下列问题,再简要说说在求解过程中有哪些疑惑.
水库的水位在最近5小时内持续上涨,右表记录了这5小时的水位高度.其中 t 表示时间,y 表示水位高度.
t/h 0 1 2 3 4 5
y/m 4 4.3 4.7 5.0 5.3 5.6
①在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
②水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数
解析式,并画出函数图象.这个函数能表示水位的变化规律吗?
③据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
活动探究
学习目标
当堂检测
课堂总结
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
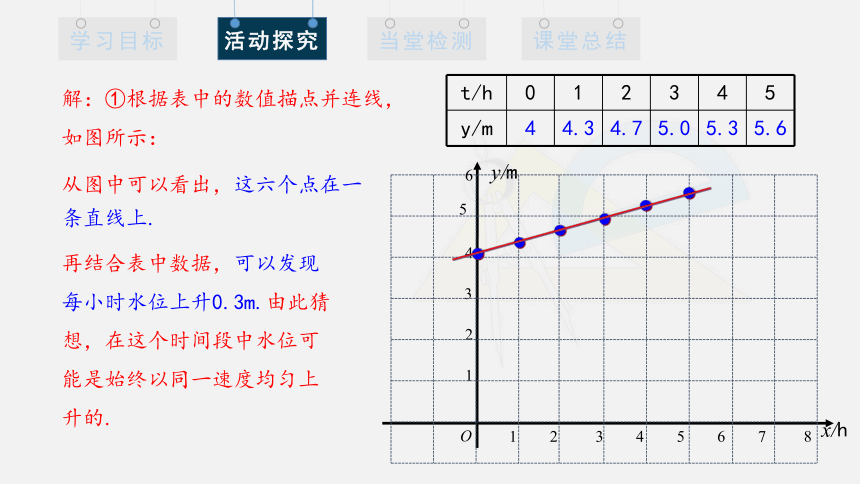
解:①根据表中的数值描点并连线,
如图所示:
从图中可以看出,这六个点在一条直线上.
再结合表中数据,可以发现每小时水位上升0.3m.由此猜想,在这个时间段中水位可能是始终以同一速度均匀上升的.
6
t/h 0 1 2 3 4 5
y/m 4 4.3 4.7 5.0 5.3 5.6
活动探究
学习目标
当堂检测
课堂总结
②由于水位在最近5 h内持续上涨,对于时间t的每一个确定的值,水位高度y都有唯一的值与其对应,所以y是t的函数.
开始水位高度为3 m,以后每小时水位上升0.3 m.所以函数解析式为:
y=0.3t+4(0≤t≤5)
②水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数
解析式,并画出函数图象.这个函数能表示水位的变化规律吗?
t/h 0 1 2 3 4 5
y/m 4 4.3 4.7 5.0 5.3 5.6
活动探究
学习目标
当堂检测
课堂总结
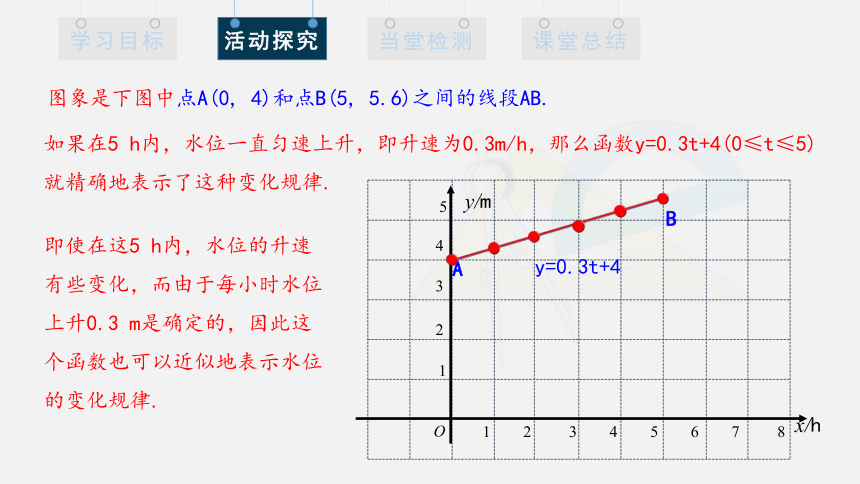
图象是下图中点A(0, 4)和点B(5, 5.6)之间的线段AB.
A
B
如果在5 h内,水位一直匀速上升,即升速为0.3m/h,那么函数y=0.3t+4(0≤t≤5)就精确地表示了这种变化规律.
即使在这5 h内,水位的升速有些变化,而由于每小时水位上升0.3 m是确定的,因此这个函数也可以近似地表示水位的变化规律.
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
y=0.3t+4
活动探究
学习目标
当堂检测
课堂总结
③据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
解:如果水位的变化规律不变,
按上述函数预测,再持续2小时,
即t=5+2=7(h)时,水位高度
y=0.3×7+4=6.1(m)
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
A
B
此时函数图象(线段AB)向右
延伸到对应的位置,这时水位
高度约为6.1m.
活动探究
学习目标
当堂检测
课堂总结
小组讨论
1.在表示“水位上涨”问题中水位高度 y 和时间 t 之间的函数关系时,用到了哪些方法?在预测2小时后的水位高度时,通过图象估算和通过解析式求出哪种方法比较好?
2.函数的三种表示方法各有什么优势或特点?它们之间是否可以转化?你能结合水位上涨问题说说你的看法吗
活动探究
学习目标
当堂检测
课堂总结
活动小结
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系.
3.图象法:直观地反映了函数随自变量的变化而变化的规律.
三种表示函数的方法的特点:
表达函数时,要根据具体情况选择适当的方法,有时为全面地认识问题,需要同时使用几种方法.
活动探究
学习目标
当堂检测
课堂总结
任务二:运用函数的三种表示方法解决相关问题
活动:如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,请求出它们的函数解析式,并写出自变量
的取值范围.
(2)当x的值分别为1,2,3,4,5,6时,
请填写右表,并画出函数的图象.
x
x/m 1 2 3 4 5 6
y/m
活动探究
学习目标
当堂检测
课堂总结
则 y =2(x + )
解:(1)周长=[(面积÷一边长)+另一边长]×2
x
面积为12 m2
周长为 y m
(1)变量 y 是变量 x 的函数吗?如果是,请求出它们的函数解析式,并写出
自变量的取值范围.
(2)当x的值分别为1,2,3,4,5,6时,请列表
表示变量之间的对应关系,并画出函数的图象.
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
(2)填表、作图如下:
40
35
30
25
20
15
10
5
5
10
O
x
y
y =2(x + )
(其中x>0)
1.用解析式法与图象法表示等边三角形的周长l是边长a的函数.
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为l=3a(a>0).
用描点法画函数l=3a的图象.
a … 1 2 3 4 …
l … …
描点、连线:
3
6
9
12
O
2
x
y
1
2
3
4
5
8
6
4
10
12
l=3a
2.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离s是时间t的函数吗?如果是,写出函数的解析式,并画出函数图象,如果船速不变,多长时间到达码头?
解:小船与码头的距离是时间的函数,小船每前进2min,与码头的
距离就减少50m,据此可得表达式为:
s = 200-25t(0≤t≤8)
s = 200-25t
① 列表:
t/min 0 2 4 6 8
s/m 200 150 100 50 0
② 描点:
③ 连线:
s = 200-25t
由函数解析式(或图象)可得,当船速不变,8min后船到达码头.
针对本节课的关键词“函数的表示方法”,说说你都学到了哪些知识?
第十九章 一次函数
19.1.2 函数的图象
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解函数的三种表示方法及其优缺点.
2.能用适当的方式表示实际问题中的变量之间的函数关系,解决与函数相关的简单问题.
活动探究
学习目标
当堂检测
课堂总结
任务一:结合具体实例,理解函数的三种表示方法及其优缺点.
活动1:请解决下列问题:
(1)阅读教材79页练习后的一段话,说一说表示函数的方法有哪些.
新知生成
表示函数的方法有以下三种:解析式法、列表法、图象法.它们分别
从数和形的角度反映了函数的本质.
活动探究
学习目标
当堂检测
课堂总结
(2)小组合作先求解下列问题,再简要说说在求解过程中有哪些疑惑.
水库的水位在最近5小时内持续上涨,右表记录了这5小时的水位高度.其中 t 表示时间,y 表示水位高度.
t/h 0 1 2 3 4 5
y/m 4 4.3 4.7 5.0 5.3 5.6
①在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
②水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数
解析式,并画出函数图象.这个函数能表示水位的变化规律吗?
③据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
活动探究
学习目标
当堂检测
课堂总结
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
解:①根据表中的数值描点并连线,
如图所示:
从图中可以看出,这六个点在一条直线上.
再结合表中数据,可以发现每小时水位上升0.3m.由此猜想,在这个时间段中水位可能是始终以同一速度均匀上升的.
6
t/h 0 1 2 3 4 5
y/m 4 4.3 4.7 5.0 5.3 5.6
活动探究
学习目标
当堂检测
课堂总结
②由于水位在最近5 h内持续上涨,对于时间t的每一个确定的值,水位高度y都有唯一的值与其对应,所以y是t的函数.
开始水位高度为3 m,以后每小时水位上升0.3 m.所以函数解析式为:
y=0.3t+4(0≤t≤5)
②水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数
解析式,并画出函数图象.这个函数能表示水位的变化规律吗?
t/h 0 1 2 3 4 5
y/m 4 4.3 4.7 5.0 5.3 5.6
活动探究
学习目标
当堂检测
课堂总结
图象是下图中点A(0, 4)和点B(5, 5.6)之间的线段AB.
A
B
如果在5 h内,水位一直匀速上升,即升速为0.3m/h,那么函数y=0.3t+4(0≤t≤5)就精确地表示了这种变化规律.
即使在这5 h内,水位的升速有些变化,而由于每小时水位上升0.3 m是确定的,因此这个函数也可以近似地表示水位的变化规律.
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
y=0.3t+4
活动探究
学习目标
当堂检测
课堂总结
③据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
解:如果水位的变化规律不变,
按上述函数预测,再持续2小时,
即t=5+2=7(h)时,水位高度
y=0.3×7+4=6.1(m)
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
A
B
此时函数图象(线段AB)向右
延伸到对应的位置,这时水位
高度约为6.1m.
活动探究
学习目标
当堂检测
课堂总结
小组讨论
1.在表示“水位上涨”问题中水位高度 y 和时间 t 之间的函数关系时,用到了哪些方法?在预测2小时后的水位高度时,通过图象估算和通过解析式求出哪种方法比较好?
2.函数的三种表示方法各有什么优势或特点?它们之间是否可以转化?你能结合水位上涨问题说说你的看法吗
活动探究
学习目标
当堂检测
课堂总结
活动小结
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系.
3.图象法:直观地反映了函数随自变量的变化而变化的规律.
三种表示函数的方法的特点:
表达函数时,要根据具体情况选择适当的方法,有时为全面地认识问题,需要同时使用几种方法.
活动探究
学习目标
当堂检测
课堂总结
任务二:运用函数的三种表示方法解决相关问题
活动:如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,请求出它们的函数解析式,并写出自变量
的取值范围.
(2)当x的值分别为1,2,3,4,5,6时,
请填写右表,并画出函数的图象.
x
x/m 1 2 3 4 5 6
y/m
活动探究
学习目标
当堂检测
课堂总结
则 y =2(x + )
解:(1)周长=[(面积÷一边长)+另一边长]×2
x
面积为12 m2
周长为 y m
(1)变量 y 是变量 x 的函数吗?如果是,请求出它们的函数解析式,并写出
自变量的取值范围.
(2)当x的值分别为1,2,3,4,5,6时,请列表
表示变量之间的对应关系,并画出函数的图象.
x/m 1 2 3 4 5 6
y/m
26
16
14
14
14.8
16
(2)填表、作图如下:
40
35
30
25
20
15
10
5
5
10
O
x
y
y =2(x + )
(其中x>0)
1.用解析式法与图象法表示等边三角形的周长l是边长a的函数.
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为l=3a(a>0).
用描点法画函数l=3a的图象.
a … 1 2 3 4 …
l … …
描点、连线:
3
6
9
12
O
2
x
y
1
2
3
4
5
8
6
4
10
12
l=3a
2.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离s是时间t的函数吗?如果是,写出函数的解析式,并画出函数图象,如果船速不变,多长时间到达码头?
解:小船与码头的距离是时间的函数,小船每前进2min,与码头的
距离就减少50m,据此可得表达式为:
s = 200-25t(0≤t≤8)
s = 200-25t
① 列表:
t/min 0 2 4 6 8
s/m 200 150 100 50 0
② 描点:
③ 连线:
s = 200-25t
由函数解析式(或图象)可得,当船速不变,8min后船到达码头.
针对本节课的关键词“函数的表示方法”,说说你都学到了哪些知识?
