四年级数学下册人教版10.3 总复习 观察图形、三角形、图形的运动课件(34张PPT)
文档属性
| 名称 | 四年级数学下册人教版10.3 总复习 观察图形、三角形、图形的运动课件(34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览



文档简介
(共34张PPT)
第10单元 总复习
观察图形、三角形、图形的运动
这学期学过哪些与图形有关的知识?
说一说
观察图形
三角形
图形的运动
辨认从不同位置观察一个用正方体搭成的物体所看到的图形
观
察
物
体
从同一位置观察由相同个数的正方体摆成的不同形状的物体
两点间的距离
三
角
形
三角形的定义
三角形三边的关系
三角形的高
三角形的特性
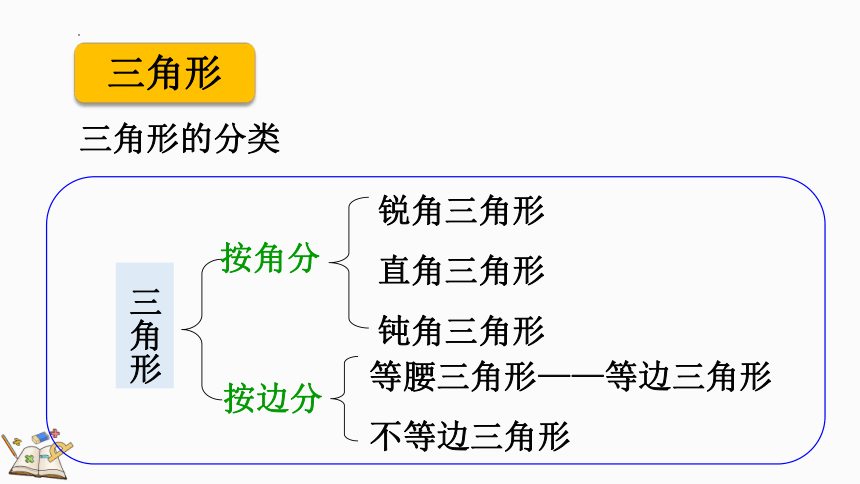
三角形的分类
三角形的内角和
多边形的内角和
图
形
的
运
动
轴对称图形的性质
根据对称轴补全轴对称图形
在方格图中确定图形平移的方向、距离
平移的应用
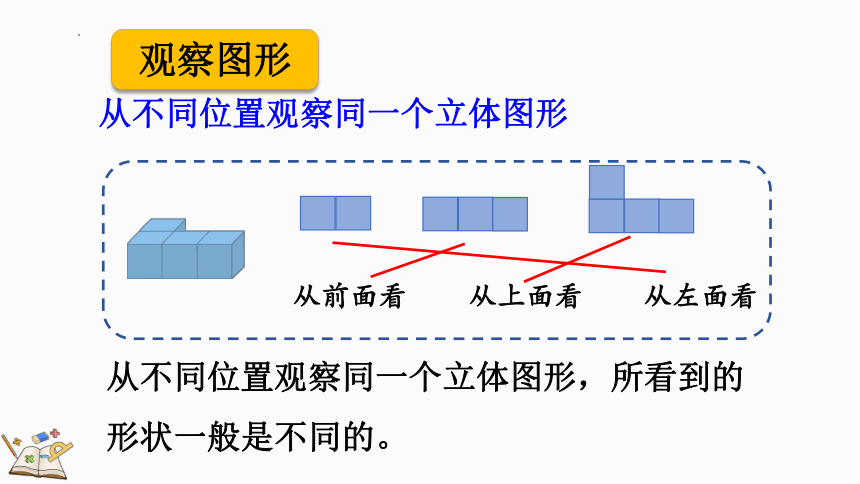
从不同位置观察同一个立体图形,所看到的形状一般是不同的。
从前面看
从上面看
从左面看
观察图形
从不同位置观察同一个立体图形
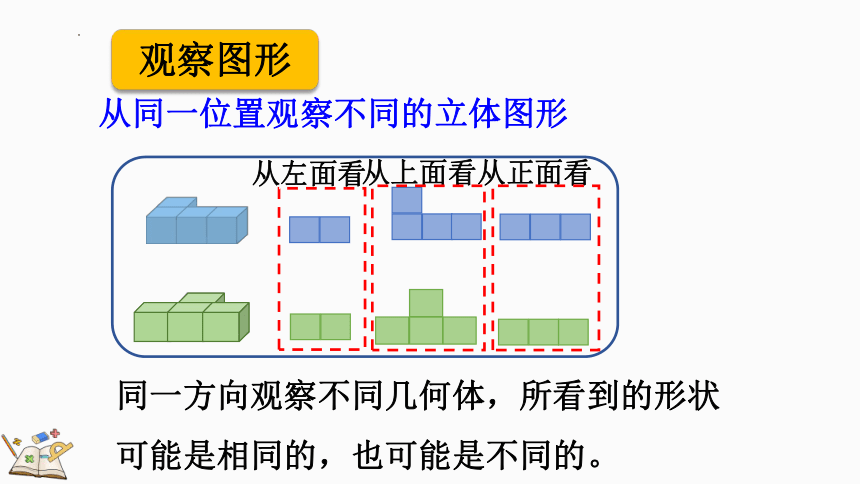
同一方向观察不同几何体,所看到的形状可能是相同的,也可能是不同的。
观察图形
从同一位置观察不同的立体图形
从左面看
从上面看
从正面看
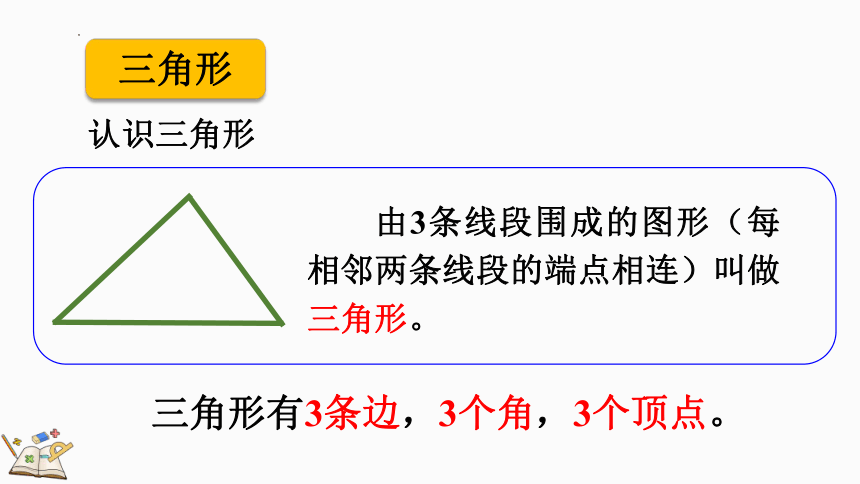
由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
三角形有3条边,3个角,3个顶点。
三角形
认识三角形
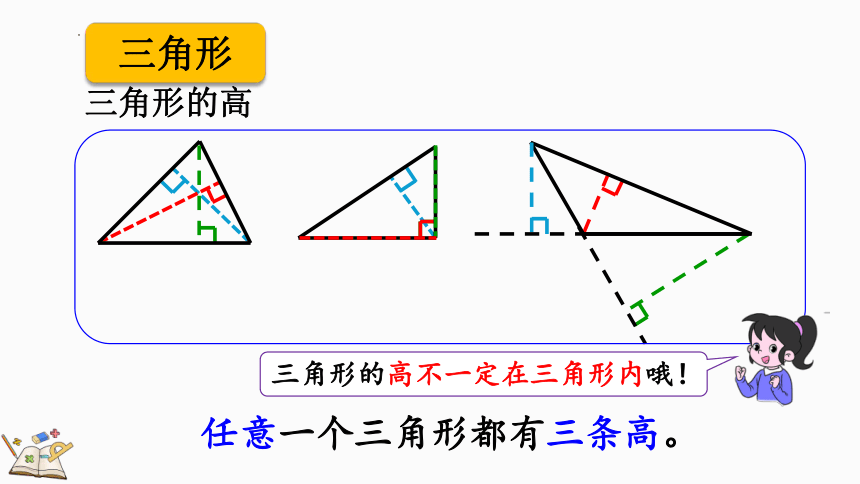
任意一个三角形都有三条高。
三角形的高
三角形
三角形的高不一定在三角形内哦!
三角形
四边形
稳定性。
容易变形。
金字塔 塔吊
推拉门
三角形的特性
三角形
三角形三边的关系
两点间所有连线中线段最短,
这条线段的长度叫做两点间的距离。
1.
三角形任意两边的和大于第三边。
2.
三角形
三角形的分类
三角形
按角分
按边分
锐角三角形
直角三角形
钝角三角形
等腰三角形——等边三角形
不等边三角形
三角形
三角形的内角和
1
2
3
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
∠1+∠2+∠3=180°
三角形的内角和是180°
三角形
3
1
2
4
周角
1
2
4
3
四边形的内角和
四边形的内角和是 360°
拼一拼
∠1+∠2+∠3+∠4
=360°
多边形的内角和
分一分
多边形所分的三角形的个数比多边形的边数少2。
多边形的内角和=180°×(边数 2)
图形的运动
轴对称图形的性质
沿对称轴将轴对称图形对折,折痕两边的部分可以完全重合。
1.
轴对称图形中,对称点的连线与对称轴垂直;对称点到对称轴的距离相等
2.
根据对称轴补全轴对称图形
找线段的端点
1.
依次连接各点,画出图形的另一半。
3.
过端点作对称轴的垂线,量出点到垂足之间的距离,确定对称点。
2.
图形的运动
平移
图形大小、形状不变。
图形的运动
图形的运动
平移的应用
通过割补、平移等方法,将不规则图形转化成规则图形。
1.
运用公式计算。
2.
在下表中适当的空格内画上“√”,再说一说几种 三角形之间的联系和区别。
图形名称 三条边都相等 只有两条边相等 有一个角是直角 只有两个锐角 有三个锐角
等腰三角形
等边三角形
锐角三角形
直角三角形
钝角三角形
√
√
√
√
√
√
√
选自教材第105页第3题
1
从前面看
从上面看
从左面看
(1)
看一看,连一连。
2
选自教材第108页练习二十五第11题
(2)
从前面看
从上面看
从左面看
选自教材第108页练习二十五第11题
看一看,连一连。
2
(1)物体( )和物体( )从上面看到的图形是相同的;
(2)这3个物体从( )面看到的图形都是相同的;
(3)这3个物体从( )面看到的图形都是不相同的。
① ② ③
填一填
3
物体 前面 上面 左面
①
②
③
① ② ③
需要判断这3个物体从不同位置看到的图形。
填一填
3
物体 前面 上面 左面
①
②
③
(1)物体( )和物体( )从上面看到的图形是相同的;
(2)这3个物体从( )面看到的图形都是相同的;
(3)这3个物体从( )面看到的图形都是不相同的。
①
③
左
前
3
情况一:假设两腰的长度各是5cm,底边长度是10cm。因为5+5=10,不符合“三角形两边之和大于第三边”,所以假设不成立。
需要分两种情况考虑。
李老师想做一个等腰三角形的教具,她需要三根小棒,目前有两根长度分别是10cm和5cm的小棒。第三根小棒的长度是( )cm。这个等腰三角形教具的周长是( )cm。
4
情况二:假设两腰的长度各是10cm,底边长度是5cm。因为10+5>10、10+10>5符合“三角形两边之和大于第三边”,所以假设成立。
第三根小棒的长度是10cm,周长:10+10+5=25cm
10
25
李老师想做一个等腰三角形的教具,她需要三根小棒,目前有两根长度分别是10cm和5cm的小棒。第三根小棒的长度是( )cm。这个等腰三角形教具的周长是( )cm。
4
A
B
C
D
E
A′
B′
C′
D′
E′
先找出每条线段的端点,数出各端点到对称轴的距离;在对称轴的另一端描出各端点的对称点;按原图形的形状顺次连接各对称点。
5
先补全下面这个轴对称图形,再画出它向右平移6格后的图形。
5
C
D
E
A
B
F
A′
B′
C′
D′
E′
F′
先找到平移前图形的关键点;把各关键点分别向右平移6格;按原图形的形状顺次连接各对称点。
先补全下面这个轴对称图形,再画出它向右平移6格后的图形。
6
公园中有一块长15米,宽8米的草坪,草坪中有一条宽2米的弯曲小路,如下图所示,铺草的面积是多少平方米?
长方形的面积就是草坪中铺草的面积。
(15-2)×8=104(平方米)
答:铺草的面积是104平方米。
15
8
2
15-2
将右边的草坪向左边平移2米,和左边的草坪重新拼成一个长方形。
在直角三角形中,∠1比∠2大30°,∠1和∠2各是多少度?
情况一:当∠1 不是直角时,那么∠2肯定也不是直角,所以∠1和∠2的和是90°,又因为∠1和∠2的差是30°,就是两个∠1的度数,进而求出∠1和∠2的度数。
∠1=(90°+30°)÷2=60°
当∠1不是直角时,
∠2=90°-60°=30°
1
情况二:当∠1 是直角时,可以根据“∠1比∠2大30°”,求出∠2的度数。
∠1=90°
当∠1是直角时,
∠2=90°-30°=60°
在直角三角形中,∠1比∠2大30°,∠1和∠2各是多少度?
1
1cm
给出的图形是不规则的多边形,要求这个图形的周长,可以先通过平移,把它转化成一个长9cm、宽4cm长方形,再计算。
(9+4)×2
=13×2
=26(厘米)
答:图形的周长是26厘米。
9
4
计算下面图形的周长。
1
观察图形
平移
三角形
观察图形、三角形、图形的运动
图形的运动
按边分
按角分
第10单元 总复习
观察图形、三角形、图形的运动
这学期学过哪些与图形有关的知识?
说一说
观察图形
三角形
图形的运动
辨认从不同位置观察一个用正方体搭成的物体所看到的图形
观
察
物
体
从同一位置观察由相同个数的正方体摆成的不同形状的物体
两点间的距离
三
角
形
三角形的定义
三角形三边的关系
三角形的高
三角形的特性
三角形的分类
三角形的内角和
多边形的内角和
图
形
的
运
动
轴对称图形的性质
根据对称轴补全轴对称图形
在方格图中确定图形平移的方向、距离
平移的应用
从不同位置观察同一个立体图形,所看到的形状一般是不同的。
从前面看
从上面看
从左面看
观察图形
从不同位置观察同一个立体图形
同一方向观察不同几何体,所看到的形状可能是相同的,也可能是不同的。
观察图形
从同一位置观察不同的立体图形
从左面看
从上面看
从正面看
由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
三角形有3条边,3个角,3个顶点。
三角形
认识三角形
任意一个三角形都有三条高。
三角形的高
三角形
三角形的高不一定在三角形内哦!
三角形
四边形
稳定性。
容易变形。
金字塔 塔吊
推拉门
三角形的特性
三角形
三角形三边的关系
两点间所有连线中线段最短,
这条线段的长度叫做两点间的距离。
1.
三角形任意两边的和大于第三边。
2.
三角形
三角形的分类
三角形
按角分
按边分
锐角三角形
直角三角形
钝角三角形
等腰三角形——等边三角形
不等边三角形
三角形
三角形的内角和
1
2
3
锐角三角形
直角三角形
钝角三角形
1
2
3
1
2
3
∠1+∠2+∠3=180°
三角形的内角和是180°
三角形
3
1
2
4
周角
1
2
4
3
四边形的内角和
四边形的内角和是 360°
拼一拼
∠1+∠2+∠3+∠4
=360°
多边形的内角和
分一分
多边形所分的三角形的个数比多边形的边数少2。
多边形的内角和=180°×(边数 2)
图形的运动
轴对称图形的性质
沿对称轴将轴对称图形对折,折痕两边的部分可以完全重合。
1.
轴对称图形中,对称点的连线与对称轴垂直;对称点到对称轴的距离相等
2.
根据对称轴补全轴对称图形
找线段的端点
1.
依次连接各点,画出图形的另一半。
3.
过端点作对称轴的垂线,量出点到垂足之间的距离,确定对称点。
2.
图形的运动
平移
图形大小、形状不变。
图形的运动
图形的运动
平移的应用
通过割补、平移等方法,将不规则图形转化成规则图形。
1.
运用公式计算。
2.
在下表中适当的空格内画上“√”,再说一说几种 三角形之间的联系和区别。
图形名称 三条边都相等 只有两条边相等 有一个角是直角 只有两个锐角 有三个锐角
等腰三角形
等边三角形
锐角三角形
直角三角形
钝角三角形
√
√
√
√
√
√
√
选自教材第105页第3题
1
从前面看
从上面看
从左面看
(1)
看一看,连一连。
2
选自教材第108页练习二十五第11题
(2)
从前面看
从上面看
从左面看
选自教材第108页练习二十五第11题
看一看,连一连。
2
(1)物体( )和物体( )从上面看到的图形是相同的;
(2)这3个物体从( )面看到的图形都是相同的;
(3)这3个物体从( )面看到的图形都是不相同的。
① ② ③
填一填
3
物体 前面 上面 左面
①
②
③
① ② ③
需要判断这3个物体从不同位置看到的图形。
填一填
3
物体 前面 上面 左面
①
②
③
(1)物体( )和物体( )从上面看到的图形是相同的;
(2)这3个物体从( )面看到的图形都是相同的;
(3)这3个物体从( )面看到的图形都是不相同的。
①
③
左
前
3
情况一:假设两腰的长度各是5cm,底边长度是10cm。因为5+5=10,不符合“三角形两边之和大于第三边”,所以假设不成立。
需要分两种情况考虑。
李老师想做一个等腰三角形的教具,她需要三根小棒,目前有两根长度分别是10cm和5cm的小棒。第三根小棒的长度是( )cm。这个等腰三角形教具的周长是( )cm。
4
情况二:假设两腰的长度各是10cm,底边长度是5cm。因为10+5>10、10+10>5符合“三角形两边之和大于第三边”,所以假设成立。
第三根小棒的长度是10cm,周长:10+10+5=25cm
10
25
李老师想做一个等腰三角形的教具,她需要三根小棒,目前有两根长度分别是10cm和5cm的小棒。第三根小棒的长度是( )cm。这个等腰三角形教具的周长是( )cm。
4
A
B
C
D
E
A′
B′
C′
D′
E′
先找出每条线段的端点,数出各端点到对称轴的距离;在对称轴的另一端描出各端点的对称点;按原图形的形状顺次连接各对称点。
5
先补全下面这个轴对称图形,再画出它向右平移6格后的图形。
5
C
D
E
A
B
F
A′
B′
C′
D′
E′
F′
先找到平移前图形的关键点;把各关键点分别向右平移6格;按原图形的形状顺次连接各对称点。
先补全下面这个轴对称图形,再画出它向右平移6格后的图形。
6
公园中有一块长15米,宽8米的草坪,草坪中有一条宽2米的弯曲小路,如下图所示,铺草的面积是多少平方米?
长方形的面积就是草坪中铺草的面积。
(15-2)×8=104(平方米)
答:铺草的面积是104平方米。
15
8
2
15-2
将右边的草坪向左边平移2米,和左边的草坪重新拼成一个长方形。
在直角三角形中,∠1比∠2大30°,∠1和∠2各是多少度?
情况一:当∠1 不是直角时,那么∠2肯定也不是直角,所以∠1和∠2的和是90°,又因为∠1和∠2的差是30°,就是两个∠1的度数,进而求出∠1和∠2的度数。
∠1=(90°+30°)÷2=60°
当∠1不是直角时,
∠2=90°-60°=30°
1
情况二:当∠1 是直角时,可以根据“∠1比∠2大30°”,求出∠2的度数。
∠1=90°
当∠1是直角时,
∠2=90°-30°=60°
在直角三角形中,∠1比∠2大30°,∠1和∠2各是多少度?
1
1cm
给出的图形是不规则的多边形,要求这个图形的周长,可以先通过平移,把它转化成一个长9cm、宽4cm长方形,再计算。
(9+4)×2
=13×2
=26(厘米)
答:图形的周长是26厘米。
9
4
计算下面图形的周长。
1
观察图形
平移
三角形
观察图形、三角形、图形的运动
图形的运动
按边分
按角分
