19.2.2 一次函数 第3课时 课件 (共16张PPT)2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 19.2.2 一次函数 第3课时 课件 (共16张PPT)2023-2024学年初中数学人教版八年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 12:14:00 | ||
图片预览






文档简介
(共16张PPT)
第十九章 一次函数
19.2.2 一次函数
第3课时
活动探究
学习目标
当堂检测
课堂总结
1.会用待定系数法求一次函数的解析式.
2.能初步应用一次函数的模型解决简单的实际问题.
活动探究
学习目标
当堂检测
课堂总结
任务一:会用待定系数法求一次函数的解析式.
活动:阅读教材P93例4,解答下列问题:
(1)函数图象上的点与其解析式有何关系?什么是待定系数法?
(2)已知一次函数的图象经过点(9,0)和(24,20),求这个一次函数的解析式.
(3)结合(1)(2)简要归纳用待定系数法求一次函数解析式的一般步骤.
活动探究
学习目标
当堂检测
课堂总结
新知生成
先设定函数解析式,再根据条件确定解析式中未知的系数,而得出函数
解析式的方法,叫做待定系数法.
函数图象上的点必定满足其函数解析式.
活动探究
学习目标
当堂检测
课堂总结
解:设这个一次函数的解析式为y=kx+b(k≠0).
∵y=kx+b的图象过点(9,0)与(24,20),
∴
解得: .
∴这个一次函数的解析式为 .
(2)已知一次函数的图象经过点(9,0)和(24,20),写出函数解析式.
活动探究
学习目标
当堂检测
课堂总结
活动小结
(1)设:设一次函数的一般形式y=kx+b(k≠0);
(2)列:把图象上的点(x1,y1),(x2,y2)代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得k,b的值;
(4)还原:把k,b的值代入一次函数的解析式.
求一次函数解析式的步骤:
活动探究
学习目标
当堂检测
课堂总结
练一练
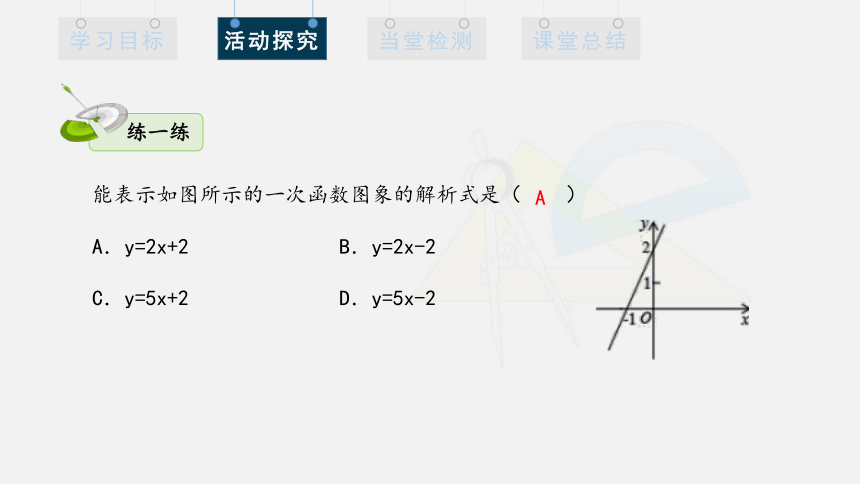
能表示如图所示的一次函数图象的解析式是( )
A.y=2x+2 B.y=2x-2
C.y=5x+2 D.y=5x-2
A
活动探究
学习目标
当堂检测
课堂总结
任务二:能初步应用一次函数的模型解决简单的实际问题.
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元
2.5
5
7.5
10
12
14
16
18
…
活动:“黄金一号”玉米种子的价格为5 元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子价格打8折.
(1)填写右表:
(2)写出付款金额关于购买量的函数解析式,并画出函数图象.(与同学比较列出
的解析式和画出的图象是否相同,图象有怎样的特点,说说你的想法)
活动探究
学习目标
当堂检测
课堂总结
=4x+2,
(2)写出付款金额关于购买量的函数解析式,并画出函数图象.
O
1
2
x
y
10
3
14
y=5x
y=4x+2
18
4
A
B
C
解:设购买量为x kg,付款金额为y 元.
当0≤x≤2时,
y=5x,
当x>2时,
y=2×5+(x-2)×5×0.8
∴付款金额关于购买量的函数解析式为:
画出函数图象是一条折线,如图所示:
y=
5x,(0≤x≤2)
4x+2,(x>2)
活动探究
学习目标
当堂检测
课堂总结
∴y=5×1.7
=22(元)
解:购买1.7 kg种子时,
∵1.7<2,
=8.5(元)
购买5 kg种子时,
∵5>2,
∴y=4×5+2
因此,购买1.7 kg种子时,需付款8.5元;
购买5 kg种子时,需付款22元.
由上面的函数解析式你能解决下列问题吗?由函数图象是否也能解决呢?
求:当分别购买1.7 kg种子和5 kg种子时,各需付款多少元.
思考
O
1
2
x
y
10
3
14
y=5x
y=4x+2,
18
4
A
B
C
,(0≤x≤2)
(x>2)
活动探究
学习目标
当堂检测
课堂总结
练一练
为缓解用电紧张的矛盾,某电力公司制定了新的用电收费标准,每月用电量
x/度与应付电费y/元的关系如图所示,根据图象求y与x的关系式.(1度=1千瓦时)
y=
,(0<x≤50)
,(x>50)
(2)如图是营销人员的月收入y(元)与该月销量x(万件)之间的函数关系图象.
由图象可知,营销员没有推销出产品时,他的月收入是 元.
1.(1)已知函数y=kx+b(k≠0)的图象与y轴交点的纵坐标为-2,且当x=2时,y=1,那么此函数的解析式为 .
1 600
(3)某市出租车收费标准如下表,设行驶x千米;出租车的运价为y元,则当
0<x≤3时,y= ;当x>3时,y与x的函数关系式为y= .
行驶路程 收费
不超过3公里 起步价6元
超过3公里部分 2.1元/km
6
2.1x-0.3
2.某校为学生装一台直饮水器,课间学生到直饮水器打水.他们先同时打开全部的水笼头放水,后来又关闭了部分水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,直饮水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题:
(1)求当x>5时,y与x之间的函数关系式;
解:设当x>5时,y关于x的函数关系式为y=kx+b,
将(5,9),(7,6)代入y=kx+b中,
解得: ,
所以x>5时,y与x之间的函数关系式为:y=-1.5x+16.5
(2)假定每人水杯接水0.7升,要使40名学生接水完毕,课间10分钟是否够用?请计算回答.
解:课间10分钟够用.
接水总量为0.7×40=28(升),
理由如下:
饮水机内剩余水量为30-28=2(升),
当y=2时,有2=-1.5x+16.5,
解得:
∵ <10
∴要使40名学生接水完毕,课间10分钟够用.
y=-1.5x+16.5
针对本节课的学习,你能回答下面的问题吗?
1.已知两点如何求一次函数的解析式?步骤有哪些?
2.已知函数图象,如何确定实际问题中的函数解析式?
第十九章 一次函数
19.2.2 一次函数
第3课时
活动探究
学习目标
当堂检测
课堂总结
1.会用待定系数法求一次函数的解析式.
2.能初步应用一次函数的模型解决简单的实际问题.
活动探究
学习目标
当堂检测
课堂总结
任务一:会用待定系数法求一次函数的解析式.
活动:阅读教材P93例4,解答下列问题:
(1)函数图象上的点与其解析式有何关系?什么是待定系数法?
(2)已知一次函数的图象经过点(9,0)和(24,20),求这个一次函数的解析式.
(3)结合(1)(2)简要归纳用待定系数法求一次函数解析式的一般步骤.
活动探究
学习目标
当堂检测
课堂总结
新知生成
先设定函数解析式,再根据条件确定解析式中未知的系数,而得出函数
解析式的方法,叫做待定系数法.
函数图象上的点必定满足其函数解析式.
活动探究
学习目标
当堂检测
课堂总结
解:设这个一次函数的解析式为y=kx+b(k≠0).
∵y=kx+b的图象过点(9,0)与(24,20),
∴
解得: .
∴这个一次函数的解析式为 .
(2)已知一次函数的图象经过点(9,0)和(24,20),写出函数解析式.
活动探究
学习目标
当堂检测
课堂总结
活动小结
(1)设:设一次函数的一般形式y=kx+b(k≠0);
(2)列:把图象上的点(x1,y1),(x2,y2)代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得k,b的值;
(4)还原:把k,b的值代入一次函数的解析式.
求一次函数解析式的步骤:
活动探究
学习目标
当堂检测
课堂总结
练一练
能表示如图所示的一次函数图象的解析式是( )
A.y=2x+2 B.y=2x-2
C.y=5x+2 D.y=5x-2
A
活动探究
学习目标
当堂检测
课堂总结
任务二:能初步应用一次函数的模型解决简单的实际问题.
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元
2.5
5
7.5
10
12
14
16
18
…
活动:“黄金一号”玉米种子的价格为5 元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子价格打8折.
(1)填写右表:
(2)写出付款金额关于购买量的函数解析式,并画出函数图象.(与同学比较列出
的解析式和画出的图象是否相同,图象有怎样的特点,说说你的想法)
活动探究
学习目标
当堂检测
课堂总结
=4x+2,
(2)写出付款金额关于购买量的函数解析式,并画出函数图象.
O
1
2
x
y
10
3
14
y=5x
y=4x+2
18
4
A
B
C
解:设购买量为x kg,付款金额为y 元.
当0≤x≤2时,
y=5x,
当x>2时,
y=2×5+(x-2)×5×0.8
∴付款金额关于购买量的函数解析式为:
画出函数图象是一条折线,如图所示:
y=
5x,(0≤x≤2)
4x+2,(x>2)
活动探究
学习目标
当堂检测
课堂总结
∴y=5×1.7
=22(元)
解:购买1.7 kg种子时,
∵1.7<2,
=8.5(元)
购买5 kg种子时,
∵5>2,
∴y=4×5+2
因此,购买1.7 kg种子时,需付款8.5元;
购买5 kg种子时,需付款22元.
由上面的函数解析式你能解决下列问题吗?由函数图象是否也能解决呢?
求:当分别购买1.7 kg种子和5 kg种子时,各需付款多少元.
思考
O
1
2
x
y
10
3
14
y=5x
y=4x+2,
18
4
A
B
C
,(0≤x≤2)
(x>2)
活动探究
学习目标
当堂检测
课堂总结
练一练
为缓解用电紧张的矛盾,某电力公司制定了新的用电收费标准,每月用电量
x/度与应付电费y/元的关系如图所示,根据图象求y与x的关系式.(1度=1千瓦时)
y=
,(0<x≤50)
,(x>50)
(2)如图是营销人员的月收入y(元)与该月销量x(万件)之间的函数关系图象.
由图象可知,营销员没有推销出产品时,他的月收入是 元.
1.(1)已知函数y=kx+b(k≠0)的图象与y轴交点的纵坐标为-2,且当x=2时,y=1,那么此函数的解析式为 .
1 600
(3)某市出租车收费标准如下表,设行驶x千米;出租车的运价为y元,则当
0<x≤3时,y= ;当x>3时,y与x的函数关系式为y= .
行驶路程 收费
不超过3公里 起步价6元
超过3公里部分 2.1元/km
6
2.1x-0.3
2.某校为学生装一台直饮水器,课间学生到直饮水器打水.他们先同时打开全部的水笼头放水,后来又关闭了部分水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,直饮水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题:
(1)求当x>5时,y与x之间的函数关系式;
解:设当x>5时,y关于x的函数关系式为y=kx+b,
将(5,9),(7,6)代入y=kx+b中,
解得: ,
所以x>5时,y与x之间的函数关系式为:y=-1.5x+16.5
(2)假定每人水杯接水0.7升,要使40名学生接水完毕,课间10分钟是否够用?请计算回答.
解:课间10分钟够用.
接水总量为0.7×40=28(升),
理由如下:
饮水机内剩余水量为30-28=2(升),
当y=2时,有2=-1.5x+16.5,
解得:
∵ <10
∴要使40名学生接水完毕,课间10分钟够用.
y=-1.5x+16.5
针对本节课的学习,你能回答下面的问题吗?
1.已知两点如何求一次函数的解析式?步骤有哪些?
2.已知函数图象,如何确定实际问题中的函数解析式?
