19.2.3 一次函数与方程、不等式 第1课时 课件(共16张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式 第1课时 课件(共16张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 11:54:41 | ||
图片预览





文档简介
(共16张PPT)
第十九章 一次函数
19.2.3 一次函数
与方程、不等式
第1课时
活动探究
学习目标
当堂检测
课堂总结
1.理解一次函数与一元一次方程、一元一次不等式之间的关系.
2.会根据一次函数的图象解决一元一次方程和一元一次不等式的求解问题.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解一次函数与一元一次方程、一元一次不等式之间的关系.
活动1:请解决下列问题:
(1)你能找出下面3个方程有什么相同点和不同点吗?
①2x+1=3; ② 2x+1=0; ③2x+1=-1.
相同点: .
不同点: .
等号左边都是2x+1
等号右边的数不同,分别是3、0、-1
(2)与同学交流,尝试从函数的角度(函数值、图象)对解这三个方程进行解释,简要归纳一元一次方程与一次函数之间的关系.
活动探究
学习目标
当堂检测
课堂总结
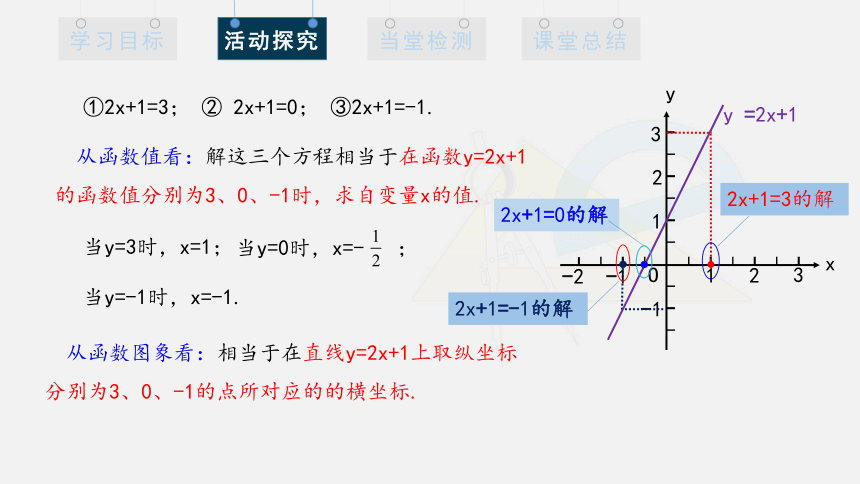
①2x+1=3; ② 2x+1=0; ③2x+1=-1.
从函数值看:解这三个方程相当于在函数y=2x+1的函数值分别为3、0、-1时,求自变量x的值.
当y=3时,x=1;
当y=0时,x=- ;
当y=-1时,x=-1.
从函数图象看:相当于在直线y=2x+1上取纵坐标
分别为3、0、-1的点所对应的的横坐标.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
2x+1=0的解
2x+1=-1的解
2x+1=3的解
活动探究
学习目标
当堂检测
课堂总结
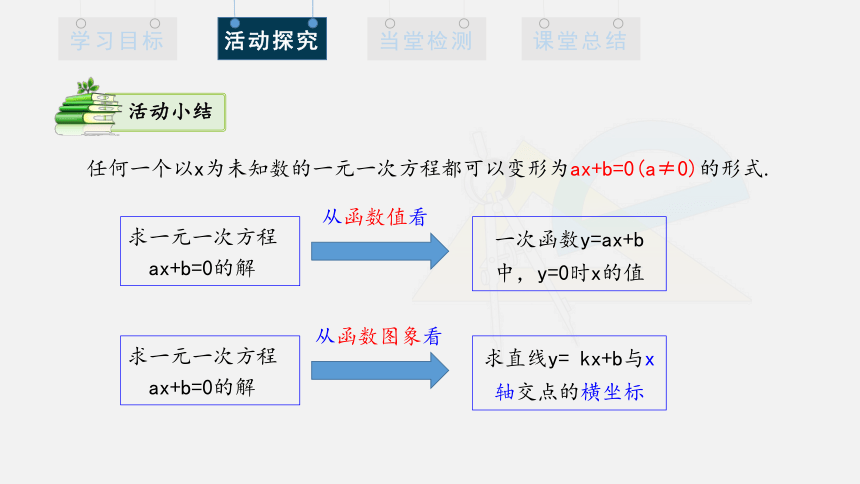
任何一个以x为未知数的一元一次方程都可以变形为ax+b=0(a≠0)的形式.
求一元一次方程
ax+b=0的解
一次函数y=ax+b
中,y=0时x的值
从函数值看
求一元一次方程
ax+b=0的解
求直线y= kx+b与x轴交点的横坐标
从函数图象看
活动小结
活动探究
学习目标
当堂检测
课堂总结
练一练
(1)直线y=2x+20与x轴交点坐标为(____,_____),这说明方程2x+20=0的解是x=_____.
(2)若方程kx+2=0的解是x=5,则直线y=kx+2与x轴交点坐标为(____,____).
-10
0
-10
5
0
活动探究
学习目标
当堂检测
课堂总结
活动2:请解决下列问题:
(1)你能找出下面3个不等式有什么相同点和不同点吗?
①3x+2>2; ②3x+2<0 ; ③3x+2<-12
相同点: .
不同点: .
等号左边都是3x+2
不等号右边的数不同,分别是2、0、-12
(2)与同学交流,从函数的角度对解这三个不等式进行解释,简要归纳一元一次不等式与一次函数之间的关系.
任务一:理解一次函数与一元一次方程、一元一次不等式之间的关系.
活动探究
学习目标
当堂检测
课堂总结
a.从函数角度看:
3x+2>2
一次函数y=3x+2大于2时自变量x的取值范围
可看做
3x+2<0
一次函数y=3x+2小于0时自变量x的取值范围
可看做
3x+2<-1
一次函数y=3x+2小于-1时自变量x的取值范围
可看做
b.从图象角度看:
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
y =2
3x+2<-1
3x+2<0
3x+2>2
y =-1
画出函数y=3x+2的图象,分别取纵
坐标满足三个条件的点,观察横坐标.
活动探究
学习目标
当堂检测
课堂总结
活动小结
任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或
ax+b<0(a≠0)的形式.
求kx+b>0(或<0)
(k≠0)的解集
y=kx+b的值大于(或小于)0时,x的取值范围
从函数值看
求kx+b>0(或<0)
(k≠0)的解集
确定直线y=kx+b在x轴上方(或下方)的图象所对应的x取值范围
从函数图象看
活动探究
学习目标
当堂检测
课堂总结
练一练
一次函数y=3x+4,y>2时,x的取值范围是 .
x>
活动探究
学习目标
当堂检测
课堂总结
活动:函数y=- x+3的图象如图所示,根据图象解答下列问题:
任务二:能通过函数的图象求解一元一次方程和一元一次不等式.
(1)求方程- x+3=0的解;
(2)求不等式- x+3>0的解集;
(3)求不等式- x+3<0的解集.
活动探究
学习目标
当堂检测
课堂总结
即 <0,
解:(1)∵直线与x轴的交点坐标为(2,0),
∴方程 的解为x=2;
(2)∵x<2时,y>0,
∴x<2时,不等式 >0,
∴不等式 >0的解集为x<2;
∴不等式 <0的解集为x>2.
(3)当x>2时,y<0,
(1)一次函数y=kx+3的图象如图1所示,则方程
kx+3=0的解为 .
(2)如图2,已知直线y=kx+b与x轴交于点(-4,0),
则当y>0时,x的取值范围是 .
x<-4
3
y=kx+3
O
y
x
3
图1
图2
x=-3
练一练
1.如图,直线y=kx+b(b>0)经过点(2,0),则关于x的不等式kx+b≥0
的解集是( )
A.x>2 B.x<2
C.x≥2 D.x≤2
D
2.在坐标系中作出函数y=2x+6的图象,利用图象解答下列问题:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>4的解集.
y=2x+6
解:函数y=2x+6的图象如右图所示:
(1)∵直线与x轴的交点坐标为(-3,0),
∴方程2x+6=0的解为x=-3;
(2)观察图象可知,直线经过点(-1,4),
所以不等式2x+6>4的解集为x>-1.
当x>-1时,y>4,
经过本节课的学习,你能简要说说一次函数与一元一次方程、一元一次不等式之间的关系吗?
第十九章 一次函数
19.2.3 一次函数
与方程、不等式
第1课时
活动探究
学习目标
当堂检测
课堂总结
1.理解一次函数与一元一次方程、一元一次不等式之间的关系.
2.会根据一次函数的图象解决一元一次方程和一元一次不等式的求解问题.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解一次函数与一元一次方程、一元一次不等式之间的关系.
活动1:请解决下列问题:
(1)你能找出下面3个方程有什么相同点和不同点吗?
①2x+1=3; ② 2x+1=0; ③2x+1=-1.
相同点: .
不同点: .
等号左边都是2x+1
等号右边的数不同,分别是3、0、-1
(2)与同学交流,尝试从函数的角度(函数值、图象)对解这三个方程进行解释,简要归纳一元一次方程与一次函数之间的关系.
活动探究
学习目标
当堂检测
课堂总结
①2x+1=3; ② 2x+1=0; ③2x+1=-1.
从函数值看:解这三个方程相当于在函数y=2x+1的函数值分别为3、0、-1时,求自变量x的值.
当y=3时,x=1;
当y=0时,x=- ;
当y=-1时,x=-1.
从函数图象看:相当于在直线y=2x+1上取纵坐标
分别为3、0、-1的点所对应的的横坐标.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
2x+1=0的解
2x+1=-1的解
2x+1=3的解
活动探究
学习目标
当堂检测
课堂总结
任何一个以x为未知数的一元一次方程都可以变形为ax+b=0(a≠0)的形式.
求一元一次方程
ax+b=0的解
一次函数y=ax+b
中,y=0时x的值
从函数值看
求一元一次方程
ax+b=0的解
求直线y= kx+b与x轴交点的横坐标
从函数图象看
活动小结
活动探究
学习目标
当堂检测
课堂总结
练一练
(1)直线y=2x+20与x轴交点坐标为(____,_____),这说明方程2x+20=0的解是x=_____.
(2)若方程kx+2=0的解是x=5,则直线y=kx+2与x轴交点坐标为(____,____).
-10
0
-10
5
0
活动探究
学习目标
当堂检测
课堂总结
活动2:请解决下列问题:
(1)你能找出下面3个不等式有什么相同点和不同点吗?
①3x+2>2; ②3x+2<0 ; ③3x+2<-12
相同点: .
不同点: .
等号左边都是3x+2
不等号右边的数不同,分别是2、0、-12
(2)与同学交流,从函数的角度对解这三个不等式进行解释,简要归纳一元一次不等式与一次函数之间的关系.
任务一:理解一次函数与一元一次方程、一元一次不等式之间的关系.
活动探究
学习目标
当堂检测
课堂总结
a.从函数角度看:
3x+2>2
一次函数y=3x+2大于2时自变量x的取值范围
可看做
3x+2<0
一次函数y=3x+2小于0时自变量x的取值范围
可看做
3x+2<-1
一次函数y=3x+2小于-1时自变量x的取值范围
可看做
b.从图象角度看:
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
y =2
3x+2<-1
3x+2<0
3x+2>2
y =-1
画出函数y=3x+2的图象,分别取纵
坐标满足三个条件的点,观察横坐标.
活动探究
学习目标
当堂检测
课堂总结
活动小结
任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或
ax+b<0(a≠0)的形式.
求kx+b>0(或<0)
(k≠0)的解集
y=kx+b的值大于(或小于)0时,x的取值范围
从函数值看
求kx+b>0(或<0)
(k≠0)的解集
确定直线y=kx+b在x轴上方(或下方)的图象所对应的x取值范围
从函数图象看
活动探究
学习目标
当堂检测
课堂总结
练一练
一次函数y=3x+4,y>2时,x的取值范围是 .
x>
活动探究
学习目标
当堂检测
课堂总结
活动:函数y=- x+3的图象如图所示,根据图象解答下列问题:
任务二:能通过函数的图象求解一元一次方程和一元一次不等式.
(1)求方程- x+3=0的解;
(2)求不等式- x+3>0的解集;
(3)求不等式- x+3<0的解集.
活动探究
学习目标
当堂检测
课堂总结
即 <0,
解:(1)∵直线与x轴的交点坐标为(2,0),
∴方程 的解为x=2;
(2)∵x<2时,y>0,
∴x<2时,不等式 >0,
∴不等式 >0的解集为x<2;
∴不等式 <0的解集为x>2.
(3)当x>2时,y<0,
(1)一次函数y=kx+3的图象如图1所示,则方程
kx+3=0的解为 .
(2)如图2,已知直线y=kx+b与x轴交于点(-4,0),
则当y>0时,x的取值范围是 .
x<-4
3
y=kx+3
O
y
x
3
图1
图2
x=-3
练一练
1.如图,直线y=kx+b(b>0)经过点(2,0),则关于x的不等式kx+b≥0
的解集是( )
A.x>2 B.x<2
C.x≥2 D.x≤2
D
2.在坐标系中作出函数y=2x+6的图象,利用图象解答下列问题:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>4的解集.
y=2x+6
解:函数y=2x+6的图象如右图所示:
(1)∵直线与x轴的交点坐标为(-3,0),
∴方程2x+6=0的解为x=-3;
(2)观察图象可知,直线经过点(-1,4),
所以不等式2x+6>4的解集为x>-1.
当x>-1时,y>4,
经过本节课的学习,你能简要说说一次函数与一元一次方程、一元一次不等式之间的关系吗?
