19.2.3 一次函数与方程、不等式 第2课时 课件(共14张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式 第2课时 课件(共14张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 16:48:55 | ||
图片预览





文档简介
(共14张PPT)
第十九章 一次函数
19.2.3 一次函数与方程、
不等式
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解一次函数与二元一次方程组的关系,会用图象法解二元
一次方程组.
2.能利用一次函数与二元一次方程组的关系解决实际问题.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解一次函数与二元一次方程组的关系.
活动1:与同学交流,解决下列问题:
(1)回顾所学简要说说什么是二元一次方程(组).
(2)请帮助y=-x+5找“座位”,它应该坐哪呢?
二元一次方程
一次函数
1
2
活动探究
学习目标
当堂检测
课堂总结
(3)请尝试用不同的方法求出一次函数y=-x+5与y=0.5x+2的交点坐标,联想
求交点坐标与求解二元一次方程组 有什么联系?
通过画函数图象和解方程组得出的结果相同.
y=-x+5
y=0.5x+2
方法1:画出图象,大致确定交点坐标(2,3).
(作图存在误差,只能得出近似值,不够准确)
方法2: 解方程组,得到解为 .
(把形的问题归结为数的解决,便捷准确)
(2,3)
活动探究
学习目标
当堂检测
课堂总结
小组讨论
结合上述过程,你能说说一次函数与二元一次方程(组)的关系吗?
如何通过画图象的方法解二元一次方程组呢?
活动探究
学习目标
当堂检测
课堂总结
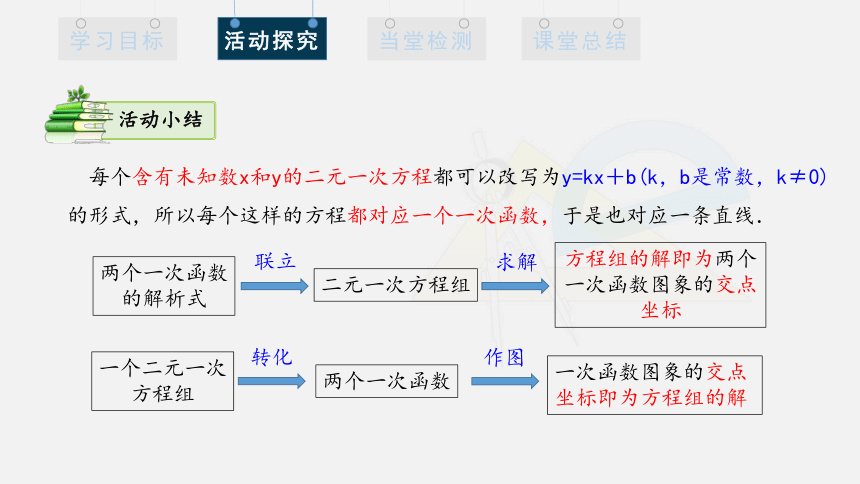
两个一次函数
的解析式
二元一次方程组
联立
求解
方程组的解即为两个
一次函数图象的交点坐标
一个二元一次
方程组
两个一次函数
转化
一次函数图象的交点坐标即为方程组的解
作图
活动小结
每个含有未知数x和y的二元一次方程都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.
活动探究
学习目标
当堂检测
课堂总结
练一练
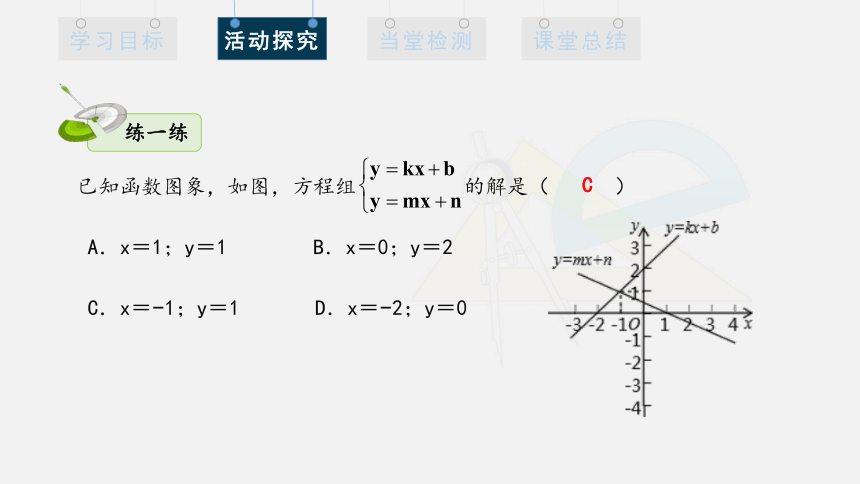
已知函数图象,如图,方程组 的解是( )
A.x=1;y=1 B.x=0;y=2
C.x= 1;y=1 D.x= 2;y=0
C
活动探究
学习目标
当堂检测
课堂总结
任务二:能利用一次函数与二元一次方程组的关系解决实际问题.
活动2:解决下列问题,简要说说你的做题思路或方法.
(1)分别表示出y1与x,y2与x的函数关系式.
(2)月通话时间为多长时,A、B两种套餐收费一样
联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐
(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月
话费为y2(元),月通话时间为x分钟.
y1 = ,y2= .
0.1x+15
0.15x
活动探究
学习目标
当堂检测
课堂总结
解:(1)A套餐的收费方式:y1=0.1x+15;
B套餐的收费方式:y2=0.15x.
(2)A、B两种套餐收费一样,则y1=y2,因此可列出二元一次方程组:
即
解得:
答:当通话时间为300分钟时,A、B两种套餐收费一样,都是45元.
1.(1)若二元一次方程组 的解为 ,则函数 与y=2x-2的图象的交点坐标为 .
(2)已知方程2x+1=x+4的解为x=3,则直线y=2x+1与y=x+4的交点为
.
(2,2)
(3,7)
2.某企业有甲、乙两个长方体蓄水池,将甲池中的水以每小时6 m3的速度注入
乙池,甲、乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数图象如图
所示,结合图象回答下列问题:
(1)分别求出甲、乙两个蓄水池中水的深度y与注水
时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池中水的深度相同.
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
解:(1)设y甲==kx+b, 把(0,2)和(3,0)代入得
设y乙==mx+n,将(0,1)和(3,4)代入得
∴ ∴y甲 =
∴ ∴y乙 = x+1.
(2)求注水多长时间甲、乙两个蓄水池中水的深度相同;
(2)根据题意,得
解得x
所以注水 小时甲、乙两个蓄水池中水的深度相同.
y=
y=x+1
针对本节课的关键词“一次函数与二元一次方程组”,说说你都学到了哪些知识?
两个一次函数
的解析式
二元一次方程组
联立
求解
方程组的解即为两个
一次函数图象的交点坐标
一个二元一次
方程组
两个一次函数
转化
一次函数图象的交点坐标即为方程组的解
作图
第十九章 一次函数
19.2.3 一次函数与方程、
不等式
第2课时
活动探究
学习目标
当堂检测
课堂总结
1.理解一次函数与二元一次方程组的关系,会用图象法解二元
一次方程组.
2.能利用一次函数与二元一次方程组的关系解决实际问题.
活动探究
学习目标
当堂检测
课堂总结
任务一:理解一次函数与二元一次方程组的关系.
活动1:与同学交流,解决下列问题:
(1)回顾所学简要说说什么是二元一次方程(组).
(2)请帮助y=-x+5找“座位”,它应该坐哪呢?
二元一次方程
一次函数
1
2
活动探究
学习目标
当堂检测
课堂总结
(3)请尝试用不同的方法求出一次函数y=-x+5与y=0.5x+2的交点坐标,联想
求交点坐标与求解二元一次方程组 有什么联系?
通过画函数图象和解方程组得出的结果相同.
y=-x+5
y=0.5x+2
方法1:画出图象,大致确定交点坐标(2,3).
(作图存在误差,只能得出近似值,不够准确)
方法2: 解方程组,得到解为 .
(把形的问题归结为数的解决,便捷准确)
(2,3)
活动探究
学习目标
当堂检测
课堂总结
小组讨论
结合上述过程,你能说说一次函数与二元一次方程(组)的关系吗?
如何通过画图象的方法解二元一次方程组呢?
活动探究
学习目标
当堂检测
课堂总结
两个一次函数
的解析式
二元一次方程组
联立
求解
方程组的解即为两个
一次函数图象的交点坐标
一个二元一次
方程组
两个一次函数
转化
一次函数图象的交点坐标即为方程组的解
作图
活动小结
每个含有未知数x和y的二元一次方程都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.
活动探究
学习目标
当堂检测
课堂总结
练一练
已知函数图象,如图,方程组 的解是( )
A.x=1;y=1 B.x=0;y=2
C.x= 1;y=1 D.x= 2;y=0
C
活动探究
学习目标
当堂检测
课堂总结
任务二:能利用一次函数与二元一次方程组的关系解决实际问题.
活动2:解决下列问题,简要说说你的做题思路或方法.
(1)分别表示出y1与x,y2与x的函数关系式.
(2)月通话时间为多长时,A、B两种套餐收费一样
联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐
(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月
话费为y2(元),月通话时间为x分钟.
y1 = ,y2= .
0.1x+15
0.15x
活动探究
学习目标
当堂检测
课堂总结
解:(1)A套餐的收费方式:y1=0.1x+15;
B套餐的收费方式:y2=0.15x.
(2)A、B两种套餐收费一样,则y1=y2,因此可列出二元一次方程组:
即
解得:
答:当通话时间为300分钟时,A、B两种套餐收费一样,都是45元.
1.(1)若二元一次方程组 的解为 ,则函数 与y=2x-2的图象的交点坐标为 .
(2)已知方程2x+1=x+4的解为x=3,则直线y=2x+1与y=x+4的交点为
.
(2,2)
(3,7)
2.某企业有甲、乙两个长方体蓄水池,将甲池中的水以每小时6 m3的速度注入
乙池,甲、乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数图象如图
所示,结合图象回答下列问题:
(1)分别求出甲、乙两个蓄水池中水的深度y与注水
时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池中水的深度相同.
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
解:(1)设y甲==kx+b, 把(0,2)和(3,0)代入得
设y乙==mx+n,将(0,1)和(3,4)代入得
∴ ∴y甲 =
∴ ∴y乙 = x+1.
(2)求注水多长时间甲、乙两个蓄水池中水的深度相同;
(2)根据题意,得
解得x
所以注水 小时甲、乙两个蓄水池中水的深度相同.
y=
y=x+1
针对本节课的关键词“一次函数与二元一次方程组”,说说你都学到了哪些知识?
两个一次函数
的解析式
二元一次方程组
联立
求解
方程组的解即为两个
一次函数图象的交点坐标
一个二元一次
方程组
两个一次函数
转化
一次函数图象的交点坐标即为方程组的解
作图
