四年级数学下册人教版10.1 总复习 四则运算的意义及其关系、运算律课件(40张PPT)
文档属性
| 名称 | 四年级数学下册人教版10.1 总复习 四则运算的意义及其关系、运算律课件(40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览









文档简介
(共40张PPT)
第十单元 总复习
四则运算的意义及
其关系、运算律
我们这学期学习了四则运算的哪些知识?
说一说
四则运算的意义
运算律
减法的性质
探究最省钱的方案
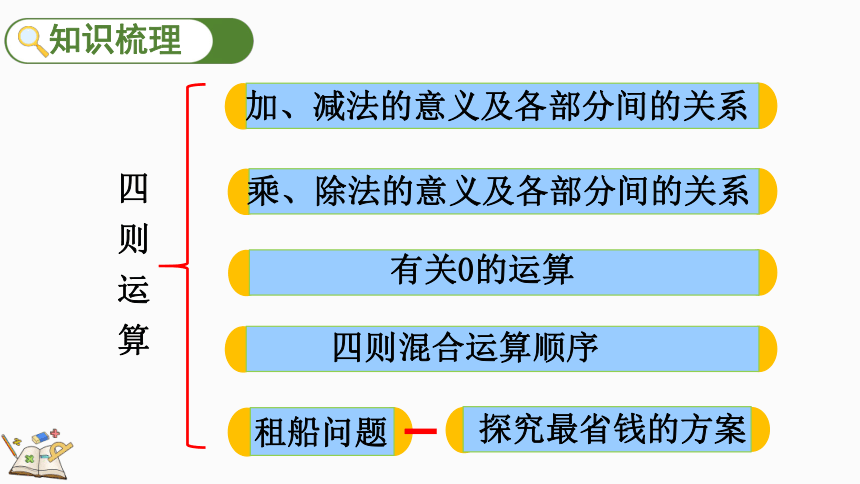
四
则
运
算
加、减法的意义及各部分间的关系
乘、除法的意义及各部分间的关系
有关0的运算
四则混合运算顺序
租船问题
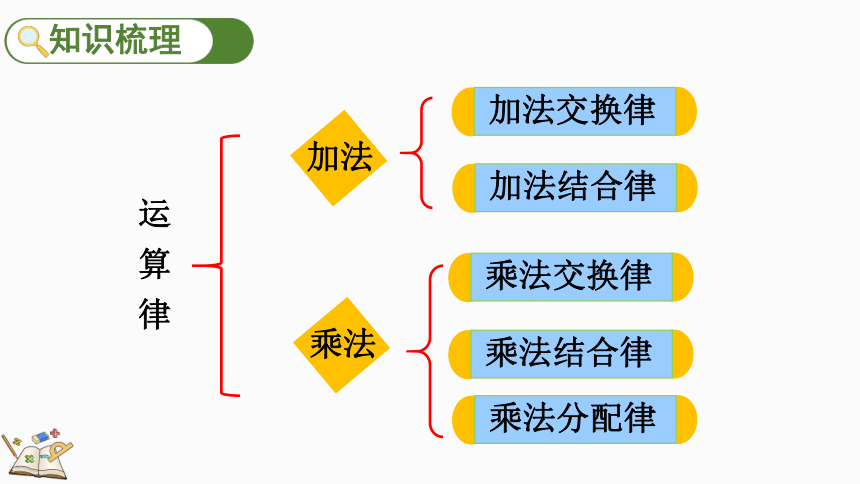
运
算
律
加法交换律
加法
乘法
加法结合律
乘法交换律
乘法结合律
乘法分配律
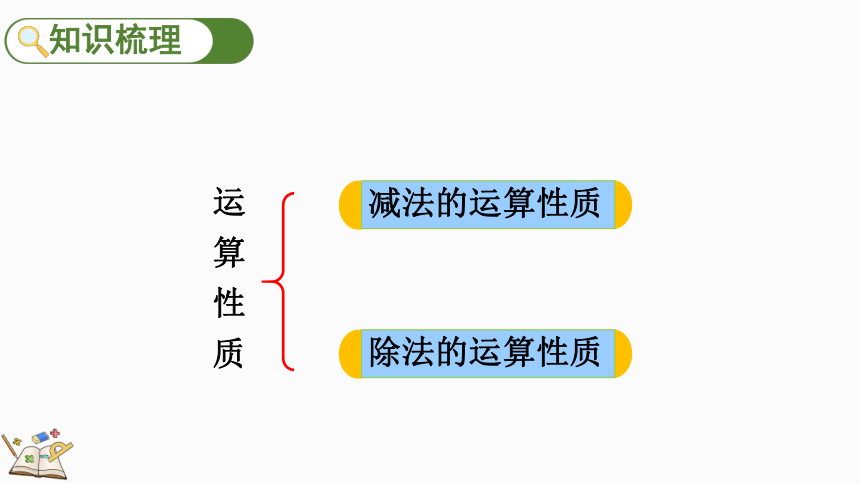
运
算
性
质
减法的运算性质
除法的运算性质
四则运算的意义和各部分之间的关系
①意义:
把两个数合并成一个数的运算,叫作加法。
②各部分的关系:
316 + 59 = 375
加数+加数=和
和-加数=另一个加数
加法的意义和各部分的关系:
四则运算的意义和各部分之间的关系
减法的意义和各部分的关系:
①意义:
已知两个数的和与其中一个加数,求另一个加数的运算,叫作减法。
②各部分的关系:
375 - 59 = 316
被减数-减数=差
被减数-差=减数
差+减数=被减数
四则运算的意义和各部分之间的关系
加法算式和减法算式各部分之间的关系:
减法是加法的逆运算。
加法算式:59+316=375
减法算式:375-59=316
或375-316=59
四则运算的意义和各部分之间的关系
乘法的意义和各部分的关系:
①意义:
求几个相同加数的和的简便运算,叫作乘法。
②各部分的关系:
25 × 8 = 200
因数×因数=积
积÷因数=另一个因数
四则运算的意义和各部分之间的关系
除法的意义和各部分的关系:
①意义:
已知两个数的积与其中一个因数,求另一个
因数的运算,叫作除法。
②各部分的关系:
375 ÷ 3 = 125
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
四则运算的意义和各部分之间的关系
乘法算式和除法算式各部分之间的关系:
除法是乘法的逆运算。
乘法算式:125×3=375
3×125=375
除法算式:375÷125=3
四则运算的意义和各部分之间的关系
(二)有关0的运算:
(1)一个数加上(或减去)0,还得原数。
(2)被减数等于减数,差是0。
(3)一个数和0相乘,仍得0。
(4)0除以一个非0的数,还得0。
四则运算的意义和各部分之间的关系
(三)四则混合运算的顺序:
没有括号,只有加、减法或只有乘、除法,
按从左往右的顺序依次计算。
没有括号,既有乘、除法,又有加、减法,
要先算乘、除法,后算加、减法。
有括号的,要先算小括号里面的,再算中
括号里面的,最后算中括号外面的。
四则运算的意义和各部分之间的关系
(四)运算律和运算性质:
运算律:
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配率:(a+b)×c=a×c+b×c
四则运算的意义和各部分之间的关系
(四)运算律和运算性质:
减法的运算性质:
①一个数连续减去两个数,相当于减去这
两个数的和: a-b-c=a-(b+c)。
②在连减运算中,任意交换两个减数的位
置,差不变: a-b-c=a-c-b。
四则运算的意义和各部分之间的关系
(四)运算律和运算性质:
除法的运算性质:
①一个数连续除以两个数,相当于除以这两
个数的积:a÷b÷c=a÷(b×c)。
②在连除运算中,任意交换两个除数的位置,
商不变:a÷b÷c=a÷c÷b。
四则运算的意义和各部分之间的关系
(五)租船问题:
探究最省钱方案:
基本方法:先假设,再确定。
选自教材第104页做一做第1题
(1)根据第①个算式,先说说加法与减法的关系,再分别写出一个加法算式和一个减法算式。
1
①316+59=375 ②375÷3=125 ③125×16=2000
加法和减法是互为逆运算的关系。
已知一个加数与和,求另一个加数
用减法计算;已知减数和差,求被
减数用加法计算。
选自教材第104页做一做第1题
加法算式:59+316=375
减法算式:375-59=316或375-316=59
1
(1)根据第①个算式,先说说加法与减法的关系,
再分别写出一个加法算式和一个减法算式。
①316+59=375 ②375÷3=125 ③125×16=2000
选自教材第104页做一做第1题
1
①316+59=375 ②375÷3=125 ③125×16=2000
(2)根据第②个算式,先说说乘法与除法的关系,
再分别写出一个乘法算式和一个除法算式。
乘法和除法是互为逆运算的关系。
已知一个因数与积,求另一个因数
用除法计算。
已知除数和商,求被除数用乘法计算。
选自教材第104页做一做第1题
1
①316+59=375 ②375÷3=125 ③125×16=2000
(2)根据第②个算式,先说说乘法与除法的关系,
再分别写出一个乘法算式和一个除法算式。
乘法算式:125×3=375或3×125=375
除法算式:375÷125=3
选自教材第104页做一做第1题
1
①316+59=375 ②375÷3=125 ③125×16=2000
(3)你会根据第①个和第②个算式列出一个综合
算式吗?再根据第①个、第②个和第③个算
式列出一个综合算式。
316+59 ÷3=125
(316+59)÷3×16=2000
( )
加、减法为第一级运算;
乘、除法为第二级运算。
1
①316+59=375 ②375÷3=125 ③125×16=2000
选自教材第104页做一做第1题
(4)下面是小明和小红的计算方法,说说他们各用了什么运算律。
加法结合律
乘法结合律
125×16
= 125×(8×2)
=(125×8)×2
= 1000×2
= 2000
316+59
= 316+(50+9)
=(316+50)+9
= 366+9
= 375
小明
小红
1
①316+59=375 ②375÷3=125 ③125×16=2000
选自教材第104页做一做第1题
(4)下面是小明和小红的计算方法,说说他们各用了什么运算律。
加法结合律
说一说我们还学过哪些运算律。
小明
小红
乘法交换律
乘法分配律
2
在 里填上适当的数,并说一说分别运用了哪些运算律。
(1)3.6+8.59+6.4=3.6+ +8.59
(2)(25.8+7.5)+2.5= +( + )
6.4
25.8
7.5
2.5
加法交换律
加法结合律
(3)42×4×25= ×( × )
(4)(125+70)×8=8× +8×
(5)(b+20)×3= × + ×
42
4
25
125
70
b
3
20
3
乘法结合律
乘法分配律
乘法分配律
2
在 里填上适当的数,并说一说分别运用了哪些运算定律。
75-29=46
1
根据加、减、乘、除法各部分间的关系,分别写
出另外两个算式。
54+38=92
92-54=38
92-38=54
75-46=29
29+46=75
1
根据加、减、乘、除法各部分间的关系,分别写
出另外两个算式。
63×30=1890
1890÷63=30
1890÷30=63
864÷24=36
864÷36=24
24×36=864
2
在 里填上合适的数,然后列出综合算式。
+
160
880
20
×
230
62
×
31
÷
550
+
1040
20800
( )
14260
460
1010
230×62
÷31
=1010
160+880
×20
=20800
550+
380-( )×8=140 ( )÷22=42……16
=
380-140=240
( )×8=240
240÷8=30
30
22×42+16=940
940
在括号中填入合适的数。
2
列竖式计算并根据加、减法或乘、除法各部分之间的关系进行验算。
456+328=
1000-275=
4 5 6
+ 3 2 8
4
1
8
7
验算
7 8 4
- 3 2 8
.
6
5
4
1 0 0 0
- 2 7 5
.
5
2
7
.
.
784
验算
7 2 5
+ 2 7 5
0
1
0
0
1
1
725
3
列竖式计算并根据加、减法或乘、除法各部分之间的关系进行验算。
3
32×125=
3 2
×1 2 5
0
1
6
1
4
6
2
3
0
0
0
4
验算
1
3 2
8
0
2
6 4
1 6
0
5
1 6 0
0
4000
1
1
4 0 0 0
3 2
324÷12=
27
3 2 4
1 2
2
2 4
8
4
7
8 4
0
验算
1 2
× 2 7
4
1
8
4
4
1
2
3
2
100÷[80÷(68-48)]
206+108÷(61-49)
=100÷[80÷20]
=100÷4
=25
=206+108÷12
=206+9
=215
减法 除法 除法
减法 除法 加法
先说一说运算顺序,再进行计算。
4
1.计算下面各题,怎样简便就怎样计算。
(1)(476-23×4)÷6
(2)846÷[6×(31-28)]
(3)4800÷25÷4
(4)56×99+56
=(476-92)÷6
= 384÷6
= 64
=846÷[6×3]
=846÷18
=47
=4800÷(25×4)
=4800÷100
=48
=56×99+56×1
=56×(99+1)
=56×100
=5600
(1)142+914+58+86
(2)35×125×8
(3)356-127-73
(4)75×101
=(142+58)+(914+86)
=200+1000
=1200
=35×(125×8)
=35×1000
=35000
=356-(127+73)
=356-200
=156
=75×(100+1)
=75×100+75×1
=7500+75
=7575
计算下面各题,怎样简便就怎样计算。
2.妈妈带了500元去超市,买了一条裤子,用去
了148元,又买了一件羊毛衫,用去了152元,
还剩下多少钱?(用两种方法解答)
方法一:
500-148-152
=352-152
=200(元)
方法二:
500-148-152
=500-(148+152)
=500-300
=200(元)
答:还剩下200元。
1.四年级3位老师带领98名同学去公园春游。
成人票:40元/人
儿童票:20元/人
团体票:30元/人
【10人以上(含10人)】
(1)怎样购票最便宜?
至少需要多少元?
可以成人和儿童分开购票,也可以购买团体票。
1.四年级3位老师带领98名同学去公园春游。
成人票:40元/人
儿童票:20元/人
团体票:30元/人
【10人以上(含10人)】
(1)怎样购票最便宜?
至少需要多少元?
分开购票:
40×3+20×98
=2080(元)
答:老师和学生分开购票最便宜,至少需要2080元。
购买团体票:
(3+98)×30
=3030(元)
2080 < 3030,因此分开购票便宜。
1.四年级3位老师带领98名同学去公园春游。
成人票:40元/人
儿童票:20元/人
团体票:30元/人
【10人以上(含10人)】
(2)如果小明一家和姑姑一家总共4名孩子、6名大人一起去玩,他们拿出300元买门票够吗?应该怎样买?
分开购票:20×4+40×6
=80+240
=320(元)
购买团体票:30×(4+6)
=30×10
=300(元)
300元<320元,因此购买团体票便宜。
答:他们应该买团体票,这样300元就够了。
四则运算和运算律
先算乘除、后算加减,有括号先算括号里面的。
加法运算律
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
乘法运算律
第十单元 总复习
四则运算的意义及
其关系、运算律
我们这学期学习了四则运算的哪些知识?
说一说
四则运算的意义
运算律
减法的性质
探究最省钱的方案
四
则
运
算
加、减法的意义及各部分间的关系
乘、除法的意义及各部分间的关系
有关0的运算
四则混合运算顺序
租船问题
运
算
律
加法交换律
加法
乘法
加法结合律
乘法交换律
乘法结合律
乘法分配律
运
算
性
质
减法的运算性质
除法的运算性质
四则运算的意义和各部分之间的关系
①意义:
把两个数合并成一个数的运算,叫作加法。
②各部分的关系:
316 + 59 = 375
加数+加数=和
和-加数=另一个加数
加法的意义和各部分的关系:
四则运算的意义和各部分之间的关系
减法的意义和各部分的关系:
①意义:
已知两个数的和与其中一个加数,求另一个加数的运算,叫作减法。
②各部分的关系:
375 - 59 = 316
被减数-减数=差
被减数-差=减数
差+减数=被减数
四则运算的意义和各部分之间的关系
加法算式和减法算式各部分之间的关系:
减法是加法的逆运算。
加法算式:59+316=375
减法算式:375-59=316
或375-316=59
四则运算的意义和各部分之间的关系
乘法的意义和各部分的关系:
①意义:
求几个相同加数的和的简便运算,叫作乘法。
②各部分的关系:
25 × 8 = 200
因数×因数=积
积÷因数=另一个因数
四则运算的意义和各部分之间的关系
除法的意义和各部分的关系:
①意义:
已知两个数的积与其中一个因数,求另一个
因数的运算,叫作除法。
②各部分的关系:
375 ÷ 3 = 125
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
四则运算的意义和各部分之间的关系
乘法算式和除法算式各部分之间的关系:
除法是乘法的逆运算。
乘法算式:125×3=375
3×125=375
除法算式:375÷125=3
四则运算的意义和各部分之间的关系
(二)有关0的运算:
(1)一个数加上(或减去)0,还得原数。
(2)被减数等于减数,差是0。
(3)一个数和0相乘,仍得0。
(4)0除以一个非0的数,还得0。
四则运算的意义和各部分之间的关系
(三)四则混合运算的顺序:
没有括号,只有加、减法或只有乘、除法,
按从左往右的顺序依次计算。
没有括号,既有乘、除法,又有加、减法,
要先算乘、除法,后算加、减法。
有括号的,要先算小括号里面的,再算中
括号里面的,最后算中括号外面的。
四则运算的意义和各部分之间的关系
(四)运算律和运算性质:
运算律:
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配率:(a+b)×c=a×c+b×c
四则运算的意义和各部分之间的关系
(四)运算律和运算性质:
减法的运算性质:
①一个数连续减去两个数,相当于减去这
两个数的和: a-b-c=a-(b+c)。
②在连减运算中,任意交换两个减数的位
置,差不变: a-b-c=a-c-b。
四则运算的意义和各部分之间的关系
(四)运算律和运算性质:
除法的运算性质:
①一个数连续除以两个数,相当于除以这两
个数的积:a÷b÷c=a÷(b×c)。
②在连除运算中,任意交换两个除数的位置,
商不变:a÷b÷c=a÷c÷b。
四则运算的意义和各部分之间的关系
(五)租船问题:
探究最省钱方案:
基本方法:先假设,再确定。
选自教材第104页做一做第1题
(1)根据第①个算式,先说说加法与减法的关系,再分别写出一个加法算式和一个减法算式。
1
①316+59=375 ②375÷3=125 ③125×16=2000
加法和减法是互为逆运算的关系。
已知一个加数与和,求另一个加数
用减法计算;已知减数和差,求被
减数用加法计算。
选自教材第104页做一做第1题
加法算式:59+316=375
减法算式:375-59=316或375-316=59
1
(1)根据第①个算式,先说说加法与减法的关系,
再分别写出一个加法算式和一个减法算式。
①316+59=375 ②375÷3=125 ③125×16=2000
选自教材第104页做一做第1题
1
①316+59=375 ②375÷3=125 ③125×16=2000
(2)根据第②个算式,先说说乘法与除法的关系,
再分别写出一个乘法算式和一个除法算式。
乘法和除法是互为逆运算的关系。
已知一个因数与积,求另一个因数
用除法计算。
已知除数和商,求被除数用乘法计算。
选自教材第104页做一做第1题
1
①316+59=375 ②375÷3=125 ③125×16=2000
(2)根据第②个算式,先说说乘法与除法的关系,
再分别写出一个乘法算式和一个除法算式。
乘法算式:125×3=375或3×125=375
除法算式:375÷125=3
选自教材第104页做一做第1题
1
①316+59=375 ②375÷3=125 ③125×16=2000
(3)你会根据第①个和第②个算式列出一个综合
算式吗?再根据第①个、第②个和第③个算
式列出一个综合算式。
316+59 ÷3=125
(316+59)÷3×16=2000
( )
加、减法为第一级运算;
乘、除法为第二级运算。
1
①316+59=375 ②375÷3=125 ③125×16=2000
选自教材第104页做一做第1题
(4)下面是小明和小红的计算方法,说说他们各用了什么运算律。
加法结合律
乘法结合律
125×16
= 125×(8×2)
=(125×8)×2
= 1000×2
= 2000
316+59
= 316+(50+9)
=(316+50)+9
= 366+9
= 375
小明
小红
1
①316+59=375 ②375÷3=125 ③125×16=2000
选自教材第104页做一做第1题
(4)下面是小明和小红的计算方法,说说他们各用了什么运算律。
加法结合律
说一说我们还学过哪些运算律。
小明
小红
乘法交换律
乘法分配律
2
在 里填上适当的数,并说一说分别运用了哪些运算律。
(1)3.6+8.59+6.4=3.6+ +8.59
(2)(25.8+7.5)+2.5= +( + )
6.4
25.8
7.5
2.5
加法交换律
加法结合律
(3)42×4×25= ×( × )
(4)(125+70)×8=8× +8×
(5)(b+20)×3= × + ×
42
4
25
125
70
b
3
20
3
乘法结合律
乘法分配律
乘法分配律
2
在 里填上适当的数,并说一说分别运用了哪些运算定律。
75-29=46
1
根据加、减、乘、除法各部分间的关系,分别写
出另外两个算式。
54+38=92
92-54=38
92-38=54
75-46=29
29+46=75
1
根据加、减、乘、除法各部分间的关系,分别写
出另外两个算式。
63×30=1890
1890÷63=30
1890÷30=63
864÷24=36
864÷36=24
24×36=864
2
在 里填上合适的数,然后列出综合算式。
+
160
880
20
×
230
62
×
31
÷
550
+
1040
20800
( )
14260
460
1010
230×62
÷31
=1010
160+880
×20
=20800
550+
380-( )×8=140 ( )÷22=42……16
=
380-140=240
( )×8=240
240÷8=30
30
22×42+16=940
940
在括号中填入合适的数。
2
列竖式计算并根据加、减法或乘、除法各部分之间的关系进行验算。
456+328=
1000-275=
4 5 6
+ 3 2 8
4
1
8
7
验算
7 8 4
- 3 2 8
.
6
5
4
1 0 0 0
- 2 7 5
.
5
2
7
.
.
784
验算
7 2 5
+ 2 7 5
0
1
0
0
1
1
725
3
列竖式计算并根据加、减法或乘、除法各部分之间的关系进行验算。
3
32×125=
3 2
×1 2 5
0
1
6
1
4
6
2
3
0
0
0
4
验算
1
3 2
8
0
2
6 4
1 6
0
5
1 6 0
0
4000
1
1
4 0 0 0
3 2
324÷12=
27
3 2 4
1 2
2
2 4
8
4
7
8 4
0
验算
1 2
× 2 7
4
1
8
4
4
1
2
3
2
100÷[80÷(68-48)]
206+108÷(61-49)
=100÷[80÷20]
=100÷4
=25
=206+108÷12
=206+9
=215
减法 除法 除法
减法 除法 加法
先说一说运算顺序,再进行计算。
4
1.计算下面各题,怎样简便就怎样计算。
(1)(476-23×4)÷6
(2)846÷[6×(31-28)]
(3)4800÷25÷4
(4)56×99+56
=(476-92)÷6
= 384÷6
= 64
=846÷[6×3]
=846÷18
=47
=4800÷(25×4)
=4800÷100
=48
=56×99+56×1
=56×(99+1)
=56×100
=5600
(1)142+914+58+86
(2)35×125×8
(3)356-127-73
(4)75×101
=(142+58)+(914+86)
=200+1000
=1200
=35×(125×8)
=35×1000
=35000
=356-(127+73)
=356-200
=156
=75×(100+1)
=75×100+75×1
=7500+75
=7575
计算下面各题,怎样简便就怎样计算。
2.妈妈带了500元去超市,买了一条裤子,用去
了148元,又买了一件羊毛衫,用去了152元,
还剩下多少钱?(用两种方法解答)
方法一:
500-148-152
=352-152
=200(元)
方法二:
500-148-152
=500-(148+152)
=500-300
=200(元)
答:还剩下200元。
1.四年级3位老师带领98名同学去公园春游。
成人票:40元/人
儿童票:20元/人
团体票:30元/人
【10人以上(含10人)】
(1)怎样购票最便宜?
至少需要多少元?
可以成人和儿童分开购票,也可以购买团体票。
1.四年级3位老师带领98名同学去公园春游。
成人票:40元/人
儿童票:20元/人
团体票:30元/人
【10人以上(含10人)】
(1)怎样购票最便宜?
至少需要多少元?
分开购票:
40×3+20×98
=2080(元)
答:老师和学生分开购票最便宜,至少需要2080元。
购买团体票:
(3+98)×30
=3030(元)
2080 < 3030,因此分开购票便宜。
1.四年级3位老师带领98名同学去公园春游。
成人票:40元/人
儿童票:20元/人
团体票:30元/人
【10人以上(含10人)】
(2)如果小明一家和姑姑一家总共4名孩子、6名大人一起去玩,他们拿出300元买门票够吗?应该怎样买?
分开购票:20×4+40×6
=80+240
=320(元)
购买团体票:30×(4+6)
=30×10
=300(元)
300元<320元,因此购买团体票便宜。
答:他们应该买团体票,这样300元就够了。
四则运算和运算律
先算乘除、后算加减,有括号先算括号里面的。
加法运算律
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
乘法运算律
